Efficient, Accurate and Stable Gradients for Neural ODEs

Neural ODEs are a recently developed model class that combine the strong model priors of differential equations with the high-capacity function approximation of neural networks. One advantage of Neural ODEs is the potential for memory-efficient training via the continuous adjoint method. However, memory-efficient training comes at the cost of approximate gradients. Therefore, in practice, gradients are often obtained by simply backpropagating through the internal operations of the forward ODE solve - incurring high memory cost. Interestingly, it is possible to construct algebraically reversible ODE solvers that allow for both exact gradients and the memory-efficiency of the continuous adjoint method. Unfortunately, current reversible solvers are low-order and suffer from poor numerical stability. The use of these methods in practice is therefore limited. In this work, we present a class of algebraically reversible solvers that are both high-order and numerically stable. Moreover, any explicit numerical scheme can be made reversible by our method. This construction naturally extends to numerical schemes for Neural CDEs and SDEs.

Physically Consistent Online Inertial Adaptation for Humanoid Loco-manipulation

The ability to accomplish manipulation and locomotion tasks in the presence of significant time-varying external loads is a remarkable skill of humans that has yet to be replicated convincingly by humanoid robots. Such an ability will be a key requirement in the environments we envision deploying our robots: dull, dirty, and dangerous. External loads constitute a large model bias, which is typically unaccounted for. In this work, we enable our humanoid robot to engage in loco-manipulation tasks in the presence of significant model bias due to external loads. We propose an online estimation and control framework involving the combination of a physically consistent extended Kalman filter for inertial parameter estimation coupled to a whole-body controller. We showcase our results both in simulation and in hardware, where weights are mounted on Nadia's wrist links as a proxy for engaging in tasks where large external loads are applied to the robot.

Single-seed generation of Brownian paths and integrals for adaptive and high order SDE solvers

Despite the success of adaptive time-stepping in ODE simulation, it has so far seen few applications for Stochastic Differential Equations (SDEs). To simulate SDEs adaptively, methods such as the Virtual Brownian Tree (VBT) have been developed, which can generate Brownian motion (BM) non-chronologically. However, in most applications, knowing only the values of Brownian motion is not enough to achieve a high order of convergence; for that, we must compute time-integrals of BM such as $\int_s^t W_r \, dr$. With the aim of using high order SDE solvers adaptively, we extend the VBT to generate these integrals of BM in addition to the Brownian increments. A JAX-based implementation of our construction is included in the popular Diffrax library (https://github.com/patrick-kidger/diffrax). Since the entire Brownian path produced by VBT is uniquely determined by a single PRNG seed, previously generated samples need not be stored, which results in a constant memory footprint and enables experiment repeatability and strong error estimation. Based on binary search, the VBT's time complexity is logarithmic in the tolerance parameter $\varepsilon$. Unlike the original VBT algorithm, which was only precise at some dyadic times, we prove that our construction exactly matches the joint distribution of the Brownian motion and its time integrals at any query times, provided they are at least $\varepsilon$ apart. We present two applications of adaptive high order solvers enabled by our new VBT. Using adaptive solvers to simulate a high-volatility CIR model, we achieve more than twice the convergence order of constant stepping. We apply an adaptive third order underdamped or kinetic Langevin solver to an MCMC problem, where our approach outperforms the No U-Turn Sampler, while using only a tenth of its function evaluations.

Efficient, Dynamic Locomotion through Step Placement with Straight Legs and Rolling Contacts

For humans, fast, efficient walking over flat ground represents the vast majority of locomotion that an individual experiences on a daily basis, and for an effective, real-world humanoid robot the same will likely be the case. In this work, we propose a locomotion controller for efficient walking over near-flat ground using a relatively simple, model-based controller that utilizes a novel combination of several interesting design features including an ALIP-based step adjustment strategy, stance leg length control as an alternative to center of mass height control, and rolling contact for heel-to-toe motion of the stance foot. We then present the results of this controller on our robot Nadia, both in simulation and on hardware. These results include validation of this controller's ability to perform fast, reliable forward walking at 0.75 m/s along with backwards walking, side-stepping, turning in place, and push recovery. We also present an efficiency comparison between the proposed control strategy and our baseline walking controller over three steady-state walking speeds. Lastly, we demonstrate some of the benefits of utilizing rolling contact in the stance foot, specifically the reduction of necessary positive and negative work throughout the stride.

Generative Modelling of Lévy Area for High Order SDE Simulation

It is well known that, when numerically simulating solutions to SDEs, achieving a strong convergence rate better than O(\sqrt{h}) (where h is the step size) requires the use of certain iterated integrals of Brownian motion, commonly referred to as its "L\'{e}vy areas". However, these stochastic integrals are difficult to simulate due to their non-Gaussian nature and for a d-dimensional Brownian motion with d > 2, no fast almost-exact sampling algorithm is known. In this paper, we propose L\'{e}vyGAN, a deep-learning-based model for generating approximate samples of L\'{e}vy area conditional on a Brownian increment. Due to our "Bridge-flipping" operation, the output samples match all joint and conditional odd moments exactly. Our generator employs a tailored GNN-inspired architecture, which enforces the correct dependency structure between the output distribution and the conditioning variable. Furthermore, we incorporate a mathematically principled characteristic-function based discriminator. Lastly, we introduce a novel training mechanism termed "Chen-training", which circumvents the need for expensive-to-generate training data-sets. This new training procedure is underpinned by our two main theoretical results. For 4-dimensional Brownian motion, we show that L\'{e}vyGAN exhibits state-of-the-art performance across several metrics which measure both the joint and marginal distributions. We conclude with a numerical experiment on the log-Heston model, a popular SDE in mathematical finance, demonstrating that high-quality synthetic L\'{e}vy area can lead to high order weak convergence and variance reduction when using multilevel Monte Carlo (MLMC).

Reachability Aware Capture Regions with Time Adjustment and Cross-Over for Step Recovery

For humanoid robots to live up to their potential utility, they must be able to robustly recover from instabilities. In this work, we propose a number of balance enhancements to enable the robot to both achieve specific, desired footholds in the world and adjusting the step positions and times as necessary while leveraging ankle and hip. This includes improving the calculation of capture regions for bipedal locomotion to better consider how step constraints affect the ability to recover. We then explore a new strategy for performing cross-over steps to maintain stability, which greatly enhances the variety of tracking error from which the robot may recover. Our last contribution is a strategy for time adaptation during the transfer phase for recovery. We then present these results on our humanoid robot, Nadia, in both simulation and hardware, showing the robot walking over rough terrain, recovering from external disturbances, and taking cross-over steps to maintain balance.

Efficient and Accurate Gradients for Neural SDEs

Neural SDEs combine many of the best qualities of both RNNs and SDEs: memory efficient training, high-capacity function approximation, and strong priors on model space. This makes them a natural choice for modelling many types of temporal dynamics. Training a Neural SDE (either as a VAE or as a GAN) requires backpropagating through an SDE solve. This may be done by solving a backwards-in-time SDE whose solution is the desired parameter gradients. However, this has previously suffered from severe speed and accuracy issues, due to high computational cost and numerical truncation errors. Here, we overcome these issues through several technical innovations. First, we introduce the \textit{reversible Heun method}. This is a new SDE solver that is \textit{algebraically reversible}: eliminating numerical gradient errors, and the first such solver of which we are aware. Moreover it requires half as many function evaluations as comparable solvers, giving up to a $1.98\times$ speedup. Second, we introduce the \textit{Brownian Interval}: a new, fast, memory efficient, and exact way of sampling \textit{and reconstructing} Brownian motion. With this we obtain up to a $10.6\times$ speed improvement over previous techniques, which in contrast are both approximate and relatively slow. Third, when specifically training Neural SDEs as GANs (Kidger et al. 2021), we demonstrate how SDE-GANs may be trained through careful weight clipping and choice of activation function. This reduces computational cost (giving up to a $1.87\times$ speedup) and removes the numerical truncation errors associated with gradient penalty. Altogether, we outperform the state-of-the-art by substantial margins, with respect to training speed, and with respect to classification, prediction, and MMD test metrics. We have contributed implementations of all of our techniques to the torchsde library to help facilitate their adoption.

Realistic Differentially-Private Transmission Power Flow Data Release

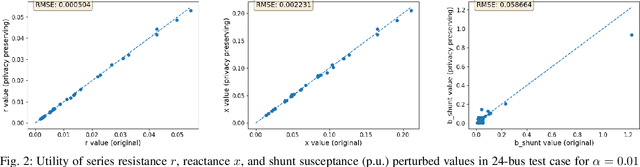
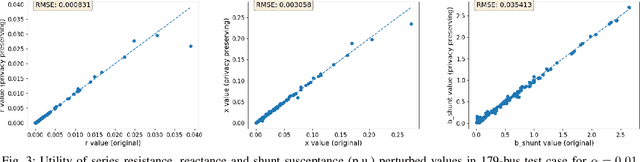
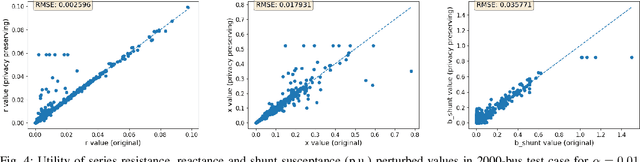
For the modeling, design and planning of future energy transmission networks, it is vital for stakeholders to access faithful and useful power flow data, while provably maintaining the privacy of business confidentiality of service providers. This critical challenge has recently been somewhat addressed in [1]. This paper significantly extends this existing work. First, we reduce the potential leakage information by proposing a fundamentally different post-processing method, using public information of grid losses rather than power dispatch, which achieve a higher level of privacy protection. Second, we protect more sensitive parameters, i.e., branch shunt susceptance in addition to series impedance (complete pi-model). This protects power flow data for the transmission high-voltage networks, using differentially private transformations that maintain the optimal power flow consistent with, and faithful to, expected model behaviour. Third, we tested our approach at a larger scale than previous work, using the PGLib-OPF test cases [10]. This resulted in the successful obfuscation of up to a 4700-bus system, which can be successfully solved with faithfulness of parameters and good utility to data analysts. Our approach addresses a more feasible and realistic scenario, and provides higher than state-of-the-art privacy guarantees, while maintaining solvability, fidelity and feasibility of the system.

Neural SDEs as Infinite-Dimensional GANs

Stochastic differential equations (SDEs) are a staple of mathematical modelling of temporal dynamics. However, a fundamental limitation has been that such models have typically been relatively inflexible, which recent work introducing Neural SDEs has sought to solve. Here, we show that the current classical approach to fitting SDEs may be approached as a special case of (Wasserstein) GANs, and in doing so the neural and classical regimes may be brought together. The input noise is Brownian motion, the output samples are time-evolving paths produced by a numerical solver, and by parameterising a discriminator as a Neural Controlled Differential Equation (CDE), we obtain Neural SDEs as (in modern machine learning parlance) continuous-time generative time series models. Unlike previous work on this problem, this is a direct extension of the classical approach without reference to either prespecified statistics or density functions. Arbitrary drift and diffusions are admissible, so as the Wasserstein loss has a unique global minima, in the infinite data limit \textit{any} SDE may be learnt.

Neural CDEs for Long Time Series via the Log-ODE Method

Neural Controlled Differential Equations (Neural CDEs) are the continuous-time analogue of an RNN, just as Neural ODEs are analogous to ResNets. However just like RNNs, training Neural CDEs can be difficult for long time series. Here, we propose to apply a technique drawn from stochastic analysis, namely the log-ODE method. Instead of using the original input sequence, our procedure summarises the information over local time intervals via the log-signature map, and uses the resulting shorter stream of log-signatures as the new input. This represents a length/channel trade-off. In doing so we demonstrate efficacy on problems of length up to 17k observations and observe significant training speed-ups, improvements in model performance, and reduced memory requirements compared to the existing algorithm.