Numerical Schemes for Signature Kernels

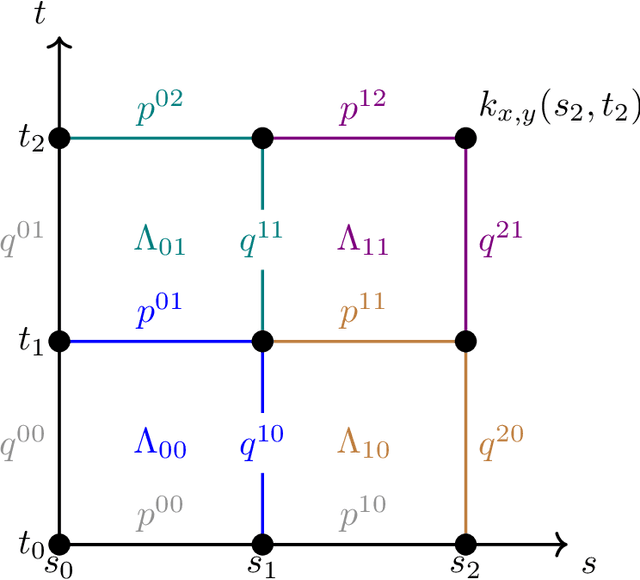
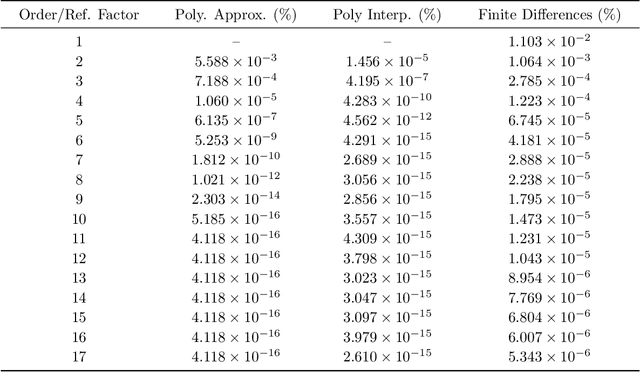
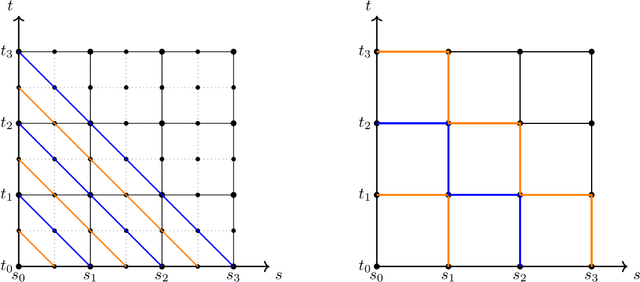
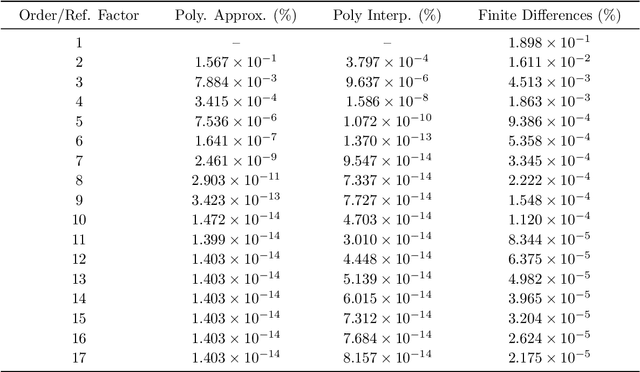
Signature kernels have emerged as a powerful tool within kernel methods for sequential data. In the paper "The Signature Kernel is the solution of a Goursat PDE", the authors identify a kernel trick that demonstrates that, for continuously differentiable paths, the signature kernel satisfies a Goursat problem for a hyperbolic partial differential equation (PDE) in two independent time variables. While finite difference methods have been explored for this PDE, they face limitations in accuracy and stability when handling highly oscillatory inputs. In this work, we introduce two advanced numerical schemes that leverage polynomial representations of boundary conditions through either approximation or interpolation techniques, and rigorously establish the theoretical convergence of the polynomial approximation scheme. Experimental evaluations reveal that our approaches yield improvements of several orders of magnitude in mean absolute percentage error (MAPE) compared to traditional finite difference schemes, without increasing computational complexity. Furthermore, like finite difference methods, our algorithms can be GPU-parallelized to reduce computational complexity from quadratic to linear in the length of the input sequences, thereby improving scalability for high-frequency data. We have implemented these algorithms in a dedicated Python library, which is publicly available at: https://github.com/FrancescoPiatti/polysigkernel.

Random Feature Representation Boosting

We introduce Random Feature Representation Boosting (RFRBoost), a novel method for constructing deep residual random feature neural networks (RFNNs) using boosting theory. RFRBoost uses random features at each layer to learn the functional gradient of the network representation, enhancing performance while preserving the convex optimization benefits of RFNNs. In the case of MSE loss, we obtain closed-form solutions to greedy layer-wise boosting with random features. For general loss functions, we show that fitting random feature residual blocks reduces to solving a quadratically constrained least squares problem. We demonstrate, through numerical experiments on 91 tabular datasets for regression and classification, that RFRBoost significantly outperforms traditional RFNNs and end-to-end trained MLP ResNets, while offering substantial computational advantages and theoretical guarantees stemming from boosting theory.

Variance Norms for Kernelized Anomaly Detection

We present a unified theory for Mahalanobis-type anomaly detection on Banach spaces, using ideas from Cameron-Martin theory applied to non-Gaussian measures. This approach leads to a basis-free, data-driven notion of anomaly distance through the so-called variance norm of a probability measure, which can be consistently estimated using empirical measures. Our framework generalizes the classical $\mathbb{R}^d$, functional $(L^2[0,1])^d$, and kernelized settings, including the general case of non-injective covariance operator. We prove that the variance norm depends solely on the inner product in a given Hilbert space, and hence that the kernelized Mahalanobis distance can naturally be recovered by working on reproducing kernel Hilbert spaces. Using the variance norm, we introduce the notion of a kernelized nearest-neighbour Mahalanobis distance for semi-supervised anomaly detection. In an empirical study on 12 real-world datasets, we demonstrate that the kernelized nearest-neighbour Mahalanobis distance outperforms the traditional kernelized Mahalanobis distance for multivariate time series anomaly detection, using state-of-the-art time series kernels such as the signature, global alignment, and Volterra reservoir kernels. Moreover, we provide an initial theoretical justification of nearest-neighbour Mahalanobis distances by developing concentration inequalities in the finite-dimensional Gaussian case.

Lecture notes on rough paths and applications to machine learning

These notes expound the recent use of the signature transform and rough path theory in data science and machine learning. We develop the core theory of the signature from first principles and then survey some recent popular applications of this approach, including signature-based kernel methods and neural rough differential equations. The notes are based on a course given by the two authors at Imperial College London.

Novelty Detection on Radio Astronomy Data using Signatures

We introduce SigNova, a new semi-supervised framework for detecting anomalies in streamed data. While our initial examples focus on detecting radio-frequency interference (RFI) in digitized signals within the field of radio astronomy, it is important to note that SigNova's applicability extends to any type of streamed data. The framework comprises three primary components. Firstly, we use the signature transform to extract a canonical collection of summary statistics from observational sequences. This allows us to represent variable-length visibility samples as finite-dimensional feature vectors. Secondly, each feature vector is assigned a novelty score, calculated as the Mahalanobis distance to its nearest neighbor in an RFI-free training set. By thresholding these scores we identify observation ranges that deviate from the expected behavior of RFI-free visibility samples without relying on stringent distributional assumptions. Thirdly, we integrate this anomaly detector with Pysegments, a segmentation algorithm, to localize consecutive observations contaminated with RFI, if any. This approach provides a compelling alternative to classical windowing techniques commonly used for RFI detection. Importantly, the complexity of our algorithm depends on the RFI pattern rather than on the size of the observation window. We demonstrate how SigNova improves the detection of various types of RFI (e.g., broadband and narrowband) in time-frequency visibility data. We validate our framework on the Murchison Widefield Array (MWA) telescope and simulated data and the Hydrogen Epoch of Reionization Array (HERA).

Generative Modelling of Lévy Area for High Order SDE Simulation

It is well known that, when numerically simulating solutions to SDEs, achieving a strong convergence rate better than O(\sqrt{h}) (where h is the step size) requires the use of certain iterated integrals of Brownian motion, commonly referred to as its "L\'{e}vy areas". However, these stochastic integrals are difficult to simulate due to their non-Gaussian nature and for a d-dimensional Brownian motion with d > 2, no fast almost-exact sampling algorithm is known. In this paper, we propose L\'{e}vyGAN, a deep-learning-based model for generating approximate samples of L\'{e}vy area conditional on a Brownian increment. Due to our "Bridge-flipping" operation, the output samples match all joint and conditional odd moments exactly. Our generator employs a tailored GNN-inspired architecture, which enforces the correct dependency structure between the output distribution and the conditioning variable. Furthermore, we incorporate a mathematically principled characteristic-function based discriminator. Lastly, we introduce a novel training mechanism termed "Chen-training", which circumvents the need for expensive-to-generate training data-sets. This new training procedure is underpinned by our two main theoretical results. For 4-dimensional Brownian motion, we show that L\'{e}vyGAN exhibits state-of-the-art performance across several metrics which measure both the joint and marginal distributions. We conclude with a numerical experiment on the log-Heston model, a popular SDE in mathematical finance, demonstrating that high-quality synthetic L\'{e}vy area can lead to high order weak convergence and variance reduction when using multilevel Monte Carlo (MLMC).

SigGPDE: Scaling Sparse Gaussian Processes on Sequential Data

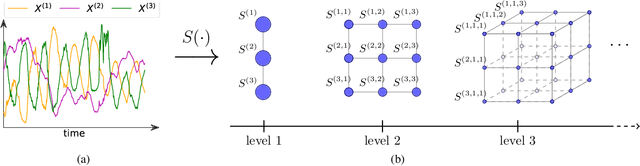
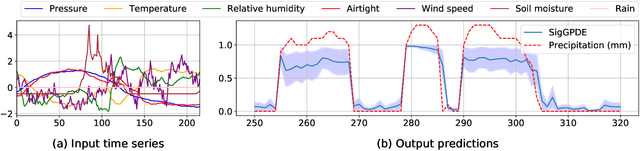
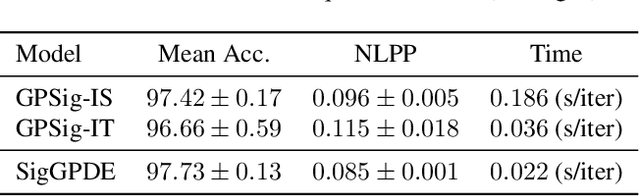
Making predictions and quantifying their uncertainty when the input data is sequential is a fundamental learning challenge, recently attracting increasing attention. We develop SigGPDE, a new scalable sparse variational inference framework for Gaussian Processes (GPs) on sequential data. Our contribution is twofold. First, we construct inducing variables underpinning the sparse approximation so that the resulting evidence lower bound (ELBO) does not require any matrix inversion. Second, we show that the gradients of the GP signature kernel are solutions of a hyperbolic partial differential equation (PDE). This theoretical insight allows us to build an efficient back-propagation algorithm to optimize the ELBO. We showcase the significant computational gains of SigGPDE compared to existing methods, while achieving state-of-the-art performance for classification tasks on large datasets of up to 1 million multivariate time series.

Computing the full signature kernel as the solution of a Goursat problem

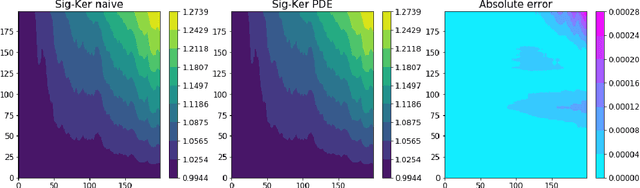
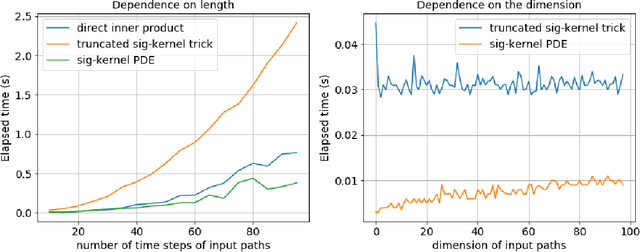
Recently there has been an increased interested in the development of kernel methods for sequential data. An inner product between the signatures of two paths can be shown to be a reproducing kernel and therefore suitable to be used in the context of data science. An efficient algorithm has been proposed to compute the signature kernel by truncating the two input signatures at a certain level, mainly focusing on the case of continuous paths of bounded variation. In this paper we show that the full (i.e. untruncated) signature kernel is the solution of a Goursat problem which can be efficiently computed by finite different schemes (python code can be found in https://github.com/crispitagorico/SignatureKernel). In practice, this result provides a kernel trick for computing the full signature kernel. Furthermore, we use a density argument to extend the previous analysis to the space of geometric rough paths, and prove using classical theory of integration of one-forms along rough paths that the full signature kernel solves a rough integral equation analogous to the PDE derived for the bounded variation case.