A High Order Solver for Signature Kernels

Signature kernels are at the core of several machine learning algorithms for analysing multivariate time series. The kernel of two bounded variation paths (such as piecewise linear interpolations of time series data) is typically computed by solving a Goursat problem for a hyperbolic partial differential equation (PDE) in two independent time variables. However, this approach becomes considerably less practical for highly oscillatory input paths, as they have to be resolved at a fine enough scale to accurately recover their signature kernel, resulting in significant time and memory complexities. To mitigate this issue, we first show that the signature kernel of a broader class of paths, known as \emph{smooth rough paths}, also satisfies a PDE, albeit in the form of a system of coupled equations. We then use this result to introduce new algorithms for the numerical approximation of signature kernels. As bounded variation paths (and more generally geometric $p$-rough paths) can be approximated by piecewise smooth rough paths, one can replace the PDE with rapidly varying coefficients in the original Goursat problem by an explicit system of coupled equations with piecewise constant coefficients derived from the first few iterated integrals of the original input paths. While this approach requires solving more equations, they do not require looking back at the complex and fine structure of the initial paths, which significantly reduces the computational complexity associated with the analysis of highly oscillatory time series.

Novelty Detection on Radio Astronomy Data using Signatures

We introduce SigNova, a new semi-supervised framework for detecting anomalies in streamed data. While our initial examples focus on detecting radio-frequency interference (RFI) in digitized signals within the field of radio astronomy, it is important to note that SigNova's applicability extends to any type of streamed data. The framework comprises three primary components. Firstly, we use the signature transform to extract a canonical collection of summary statistics from observational sequences. This allows us to represent variable-length visibility samples as finite-dimensional feature vectors. Secondly, each feature vector is assigned a novelty score, calculated as the Mahalanobis distance to its nearest neighbor in an RFI-free training set. By thresholding these scores we identify observation ranges that deviate from the expected behavior of RFI-free visibility samples without relying on stringent distributional assumptions. Thirdly, we integrate this anomaly detector with Pysegments, a segmentation algorithm, to localize consecutive observations contaminated with RFI, if any. This approach provides a compelling alternative to classical windowing techniques commonly used for RFI detection. Importantly, the complexity of our algorithm depends on the RFI pattern rather than on the size of the observation window. We demonstrate how SigNova improves the detection of various types of RFI (e.g., broadband and narrowband) in time-frequency visibility data. We validate our framework on the Murchison Widefield Array (MWA) telescope and simulated data and the Hydrogen Epoch of Reionization Array (HERA).

Non-adversarial training of Neural SDEs with signature kernel scores

Neural SDEs are continuous-time generative models for sequential data. State-of-the-art performance for irregular time series generation has been previously obtained by training these models adversarially as GANs. However, as typical for GAN architectures, training is notoriously unstable, often suffers from mode collapse, and requires specialised techniques such as weight clipping and gradient penalty to mitigate these issues. In this paper, we introduce a novel class of scoring rules on pathspace based on signature kernels and use them as objective for training Neural SDEs non-adversarially. By showing strict properness of such kernel scores and consistency of the corresponding estimators, we provide existence and uniqueness guarantees for the minimiser. With this formulation, evaluating the generator-discriminator pair amounts to solving a system of linear path-dependent PDEs which allows for memory-efficient adjoint-based backpropagation. Moreover, because the proposed kernel scores are well-defined for paths with values in infinite dimensional spaces of functions, our framework can be easily extended to generate spatiotemporal data. Our procedure permits conditioning on a rich variety of market conditions and significantly outperforms alternative ways of training Neural SDEs on a variety of tasks including the simulation of rough volatility models, the conditional probabilistic forecasts of real-world forex pairs where the conditioning variable is an observed past trajectory, and the mesh-free generation of limit order book dynamics.

Neural signature kernels as infinite-width-depth-limits of controlled ResNets

Motivated by the paradigm of reservoir computing, we consider randomly initialized controlled ResNets defined as Euler-discretizations of neural controlled differential equations (Neural CDEs). We show that in the infinite-width-then-depth limit and under proper scaling, these architectures converge weakly to Gaussian processes indexed on some spaces of continuous paths and with kernels satisfying certain partial differential equations (PDEs) varying according to the choice of activation function. In the special case where the activation is the identity, we show that the equation reduces to a linear PDE and the limiting kernel agrees with the signature kernel of Salvi et al. (2021). In this setting, we also show that the width-depth limits commute. We name this new family of limiting kernels neural signature kernels. Finally, we show that in the infinite-depth regime, finite-width controlled ResNets converge in distribution to Neural CDEs with random vector fields which, depending on whether the weights are shared across layers, are either time-independent and Gaussian or behave like a matrix-valued Brownian motion.

Neural Stochastic Partial Differential Equations

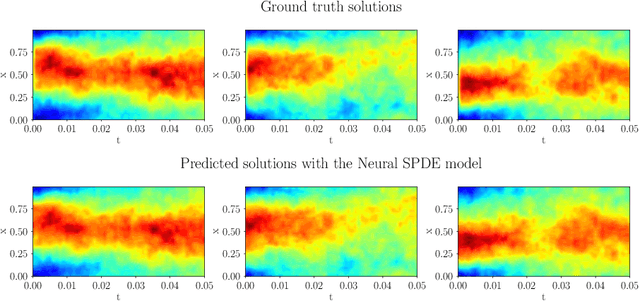
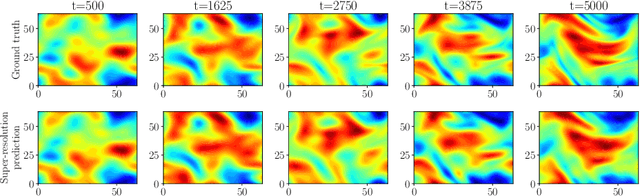
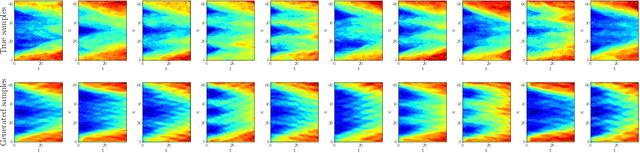
Stochastic partial differential equations (SPDEs) are the mathematical tool of choice to model complex spatio-temporal dynamics of systems subject to the influence of randomness. We introduce the Neural SPDE model providing an extension to two important classes of physics-inspired neural architectures. On the one hand, it extends all the popular neural -- ordinary, controlled, stochastic, rough -- differential equation models in that it is capable of processing incoming information even when the latter evolves in an infinite dimensional state space. On the other hand, it extends Neural Operators -- recent generalizations of neural networks modelling mappings between functional spaces -- in that it can be used to learn complex SPDE solution operators $(u_0,\xi) \mapsto u$ depending simultaneously on an initial condition $u_0$ and on a stochastic forcing term $\xi$, while remaining resolution-invariant and equation-agnostic. A Neural SPDE is constrained to respect real physical dynamics and consequently requires only a modest amount of data to train, depends on a significantly smaller amount of parameters and has better generalization properties compared to Neural Operators. Through various experiments on semilinear SPDEs with additive and multiplicative noise (including the stochastic Navier-Stokes equations) we demonstrate how Neural SPDEs can flexibly be used in a supervised learning setting as well as conditional generative models to sample solutions of SPDEs conditioned on prior knowledge, systematically achieving in both cases better performance than all alternative models.

Higher Order Kernel Mean Embeddings to Capture Filtrations of Stochastic Processes

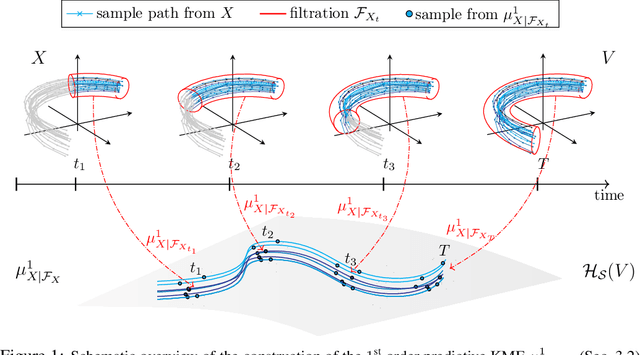
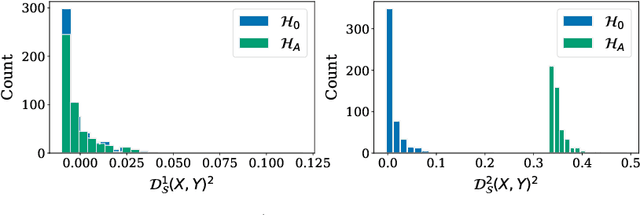
Stochastic processes are random variables with values in some space of paths. However, reducing a stochastic process to a path-valued random variable ignores its filtration, i.e. the flow of information carried by the process through time. By conditioning the process on its filtration, we introduce a family of higher order kernel mean embeddings (KMEs) that generalizes the notion of KME and captures additional information related to the filtration. We derive empirical estimators for the associated higher order maximum mean discrepancies (MMDs) and prove consistency. We then construct a filtration-sensitive kernel two-sample test able to pick up information that gets missed by the standard MMD test. In addition, leveraging our higher order MMDs we construct a family of universal kernels on stochastic processes that allows to solve real-world calibration and optimal stopping problems in quantitative finance (such as the pricing of American options) via classical kernel-based regression methods. Finally, adapting existing tests for conditional independence to the case of stochastic processes, we design a causal-discovery algorithm to recover the causal graph of structural dependencies among interacting bodies solely from observations of their multidimensional trajectories.

SigGPDE: Scaling Sparse Gaussian Processes on Sequential Data

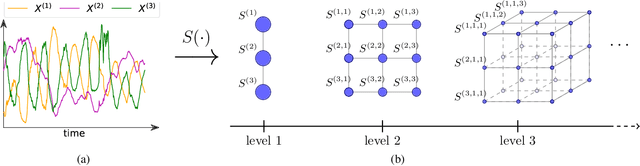
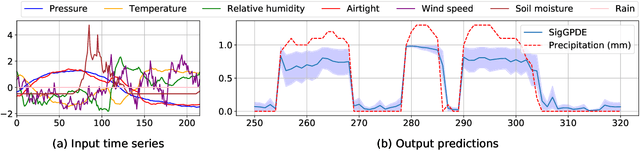
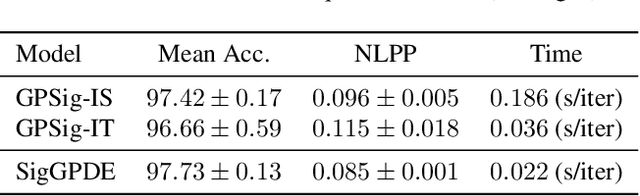
Making predictions and quantifying their uncertainty when the input data is sequential is a fundamental learning challenge, recently attracting increasing attention. We develop SigGPDE, a new scalable sparse variational inference framework for Gaussian Processes (GPs) on sequential data. Our contribution is twofold. First, we construct inducing variables underpinning the sparse approximation so that the resulting evidence lower bound (ELBO) does not require any matrix inversion. Second, we show that the gradients of the GP signature kernel are solutions of a hyperbolic partial differential equation (PDE). This theoretical insight allows us to build an efficient back-propagation algorithm to optimize the ELBO. We showcase the significant computational gains of SigGPDE compared to existing methods, while achieving state-of-the-art performance for classification tasks on large datasets of up to 1 million multivariate time series.

Distribution Regression for Continuous-Time Processes via the Expected Signature

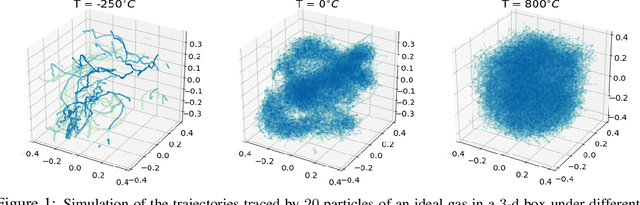
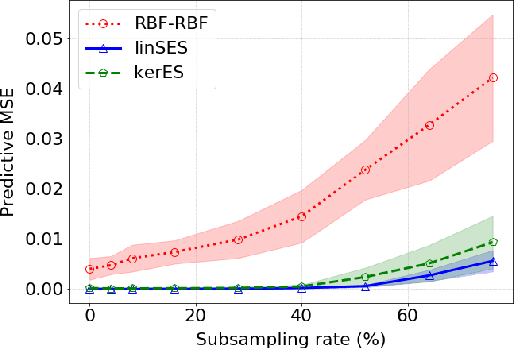
We introduce a learning framework to infer macroscopic properties of an evolving system from longitudinal trajectories of its components. By considering probability measures on continuous paths we view this problem as a distribution regression task for continuous-time processes and propose two distinct solutions leveraging the recently established properties of the expected signature. Firstly, we embed the measures in a Hilbert space, enabling the application of an existing kernel-based technique. Secondly, we recast the complex task of learning a non-linear regression function on probability measures to a simpler functional linear regression on the signature of a single vector-valued path. We provide theoretical results on the universality of both approaches, and demonstrate empirically their robustness to densely and irregularly sampled multivariate time-series, outperforming existing methods adapted to this task on both synthetic and real-world examples from thermodynamics, mathematical finance and agricultural science.