Neural Stochastic Partial Differential Equations
Paper and Code
Oct 19, 2021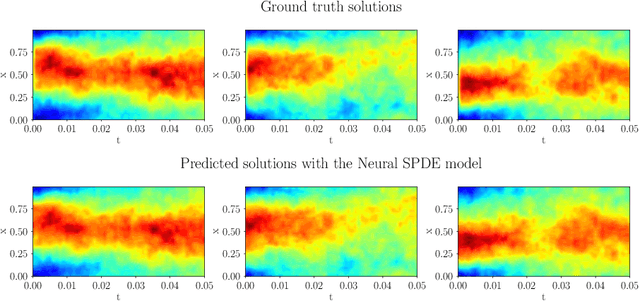

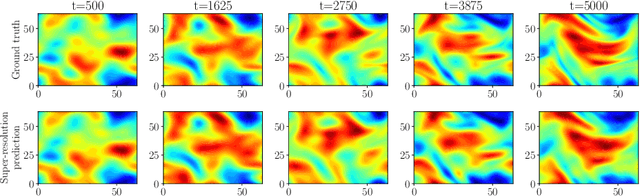
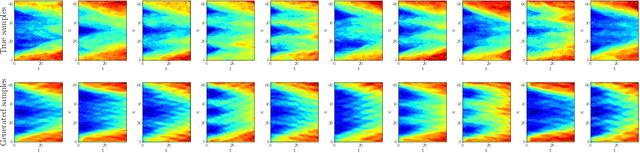
Stochastic partial differential equations (SPDEs) are the mathematical tool of choice to model complex spatio-temporal dynamics of systems subject to the influence of randomness. We introduce the Neural SPDE model providing an extension to two important classes of physics-inspired neural architectures. On the one hand, it extends all the popular neural -- ordinary, controlled, stochastic, rough -- differential equation models in that it is capable of processing incoming information even when the latter evolves in an infinite dimensional state space. On the other hand, it extends Neural Operators -- recent generalizations of neural networks modelling mappings between functional spaces -- in that it can be used to learn complex SPDE solution operators $(u_0,\xi) \mapsto u$ depending simultaneously on an initial condition $u_0$ and on a stochastic forcing term $\xi$, while remaining resolution-invariant and equation-agnostic. A Neural SPDE is constrained to respect real physical dynamics and consequently requires only a modest amount of data to train, depends on a significantly smaller amount of parameters and has better generalization properties compared to Neural Operators. Through various experiments on semilinear SPDEs with additive and multiplicative noise (including the stochastic Navier-Stokes equations) we demonstrate how Neural SPDEs can flexibly be used in a supervised learning setting as well as conditional generative models to sample solutions of SPDEs conditioned on prior knowledge, systematically achieving in both cases better performance than all alternative models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge