Neural CDEs for Long Time Series via the Log-ODE Method

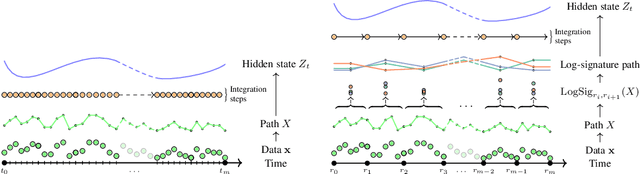
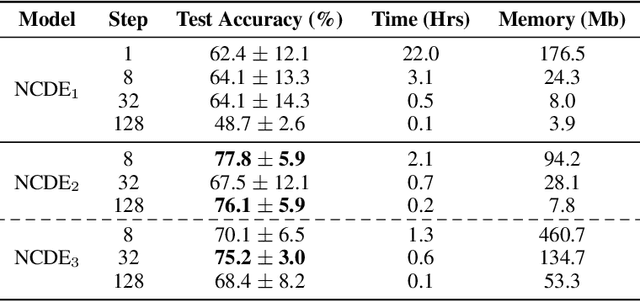
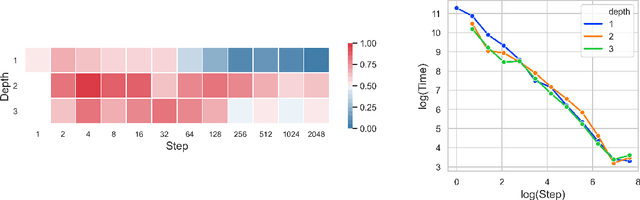
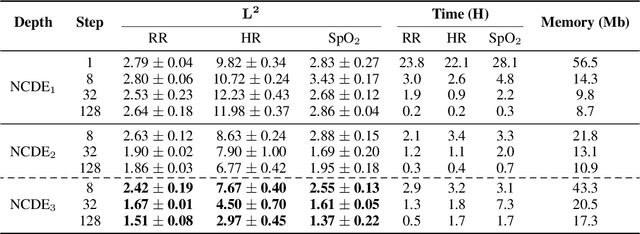
Neural Controlled Differential Equations (Neural CDEs) are the continuous-time analogue of an RNN, just as Neural ODEs are analogous to ResNets. However just like RNNs, training Neural CDEs can be difficult for long time series. Here, we propose to apply a technique drawn from stochastic analysis, namely the log-ODE method. Instead of using the original input sequence, our procedure summarises the information over local time intervals via the log-signature map, and uses the resulting shorter stream of log-signatures as the new input. This represents a length/channel trade-off. In doing so we demonstrate efficacy on problems of length up to 17k observations and observe significant training speed-ups, improvements in model performance, and reduced memory requirements compared to the existing algorithm.