A Unified View of Optimal Kernel Hypothesis Testing

This paper provides a unifying view of optimal kernel hypothesis testing across the MMD two-sample, HSIC independence, and KSD goodness-of-fit frameworks. Minimax optimal separation rates in the kernel and $L^2$ metrics are presented, with two adaptive kernel selection methods (kernel pooling and aggregation), and under various testing constraints: computational efficiency, differential privacy, and robustness to data corruption. Intuition behind the derivation of the power results is provided in a unified way accross the three frameworks, and open problems are highlighted.

A Practical Introduction to Kernel Discrepancies: MMD, HSIC & KSD

This article provides a practical introduction to kernel discrepancies, focusing on the Maximum Mean Discrepancy (MMD), the Hilbert-Schmidt Independence Criterion (HSIC), and the Kernel Stein Discrepancy (KSD). Various estimators for these discrepancies are presented, including the commonly-used V-statistics and U-statistics, as well as several forms of the more computationally-efficient incomplete U-statistics. The importance of the choice of kernel bandwidth is stressed, showing how it affects the behaviour of the discrepancy estimation. Adaptive estimators are introduced, which combine multiple estimators with various kernels, addressing the problem of kernel selection.

Credal Two-Sample Tests of Epistemic Ignorance

We introduce credal two-sample testing, a new hypothesis testing framework for comparing credal sets -- convex sets of probability measures where each element captures aleatoric uncertainty and the set itself represents epistemic uncertainty that arises from the modeller's partial ignorance. Classical two-sample tests, which rely on comparing precise distributions, fail to address epistemic uncertainty due to partial ignorance. To bridge this gap, we generalise two-sample tests to compare credal sets, enabling reasoning for equality, inclusion, intersection, and mutual exclusivity, each offering unique insights into the modeller's epistemic beliefs. We formalise these tests as two-sample tests with nuisance parameters and introduce the first permutation-based solution for this class of problems, significantly improving upon existing methods. Our approach properly incorporates the modeller's epistemic uncertainty into hypothesis testing, leading to more robust and credible conclusions, with kernel-based implementations for real-world applications.

Robust Kernel Hypothesis Testing under Data Corruption

We propose two general methods for constructing robust permutation tests under data corruption. The proposed tests effectively control the non-asymptotic type I error under data corruption, and we prove their consistency in power under minimal conditions. This contributes to the practical deployment of hypothesis tests for real-world applications with potential adversarial attacks. One of our methods inherently ensures differential privacy, further broadening its applicability to private data analysis. For the two-sample and independence settings, we show that our kernel robust tests are minimax optimal, in the sense that they are guaranteed to be non-asymptotically powerful against alternatives uniformly separated from the null in the kernel MMD and HSIC metrics at some optimal rate (tight with matching lower bound). Finally, we provide publicly available implementations and empirically illustrate the practicality of our proposed tests.

Practical Kernel Tests of Conditional Independence

We describe a data-efficient, kernel-based approach to statistical testing of conditional independence. A major challenge of conditional independence testing, absent in tests of unconditional independence, is to obtain the correct test level (the specified upper bound on the rate of false positives), while still attaining competitive test power. Excess false positives arise due to bias in the test statistic, which is obtained using nonparametric kernel ridge regression. We propose three methods for bias control to correct the test level, based on data splitting, auxiliary data, and (where possible) simpler function classes. We show these combined strategies are effective both for synthetic and real-world data.

Differentially Private Permutation Tests: Applications to Kernel Methods

Recent years have witnessed growing concerns about the privacy of sensitive data. In response to these concerns, differential privacy has emerged as a rigorous framework for privacy protection, gaining widespread recognition in both academic and industrial circles. While substantial progress has been made in private data analysis, existing methods often suffer from impracticality or a significant loss of statistical efficiency. This paper aims to alleviate these concerns in the context of hypothesis testing by introducing differentially private permutation tests. The proposed framework extends classical non-private permutation tests to private settings, maintaining both finite-sample validity and differential privacy in a rigorous manner. The power of the proposed test depends on the choice of a test statistic, and we establish general conditions for consistency and non-asymptotic uniform power. To demonstrate the utility and practicality of our framework, we focus on reproducing kernel-based test statistics and introduce differentially private kernel tests for two-sample and independence testing: dpMMD and dpHSIC. The proposed kernel tests are straightforward to implement, applicable to various types of data, and attain minimax optimal power across different privacy regimes. Our empirical evaluations further highlight their competitive power under various synthetic and real-world scenarios, emphasizing their practical value. The code is publicly available to facilitate the implementation of our framework.

MMD-FUSE: Learning and Combining Kernels for Two-Sample Testing Without Data Splitting

We propose novel statistics which maximise the power of a two-sample test based on the Maximum Mean Discrepancy (MMD), by adapting over the set of kernels used in defining it. For finite sets, this reduces to combining (normalised) MMD values under each of these kernels via a weighted soft maximum. Exponential concentration bounds are proved for our proposed statistics under the null and alternative. We further show how these kernels can be chosen in a data-dependent but permutation-independent way, in a well-calibrated test, avoiding data splitting. This technique applies more broadly to general permutation-based MMD testing, and includes the use of deep kernels with features learnt using unsupervised models such as auto-encoders. We highlight the applicability of our MMD-FUSE test on both synthetic low-dimensional and real-world high-dimensional data, and compare its performance in terms of power against current state-of-the-art kernel tests.

Discussion of `Multiscale Fisher's Independence Test for Multivariate Dependence'

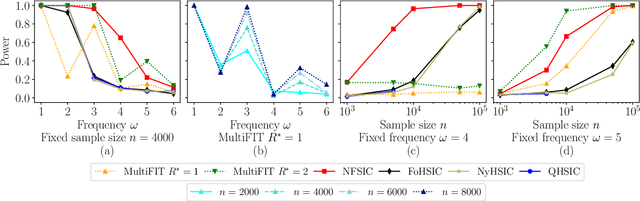
We discuss how MultiFIT, the Multiscale Fisher's Independence Test for Multivariate Dependence proposed by Gorsky and Ma (2022), compares to existing linear-time kernel tests based on the Hilbert-Schmidt independence criterion (HSIC). We highlight the fact that the levels of the kernel tests at any finite sample size can be controlled exactly, as it is the case with the level of MultiFIT. In our experiments, we observe some of the performance limitations of MultiFIT in terms of test power.

Efficient Aggregated Kernel Tests using Incomplete $U$-statistics

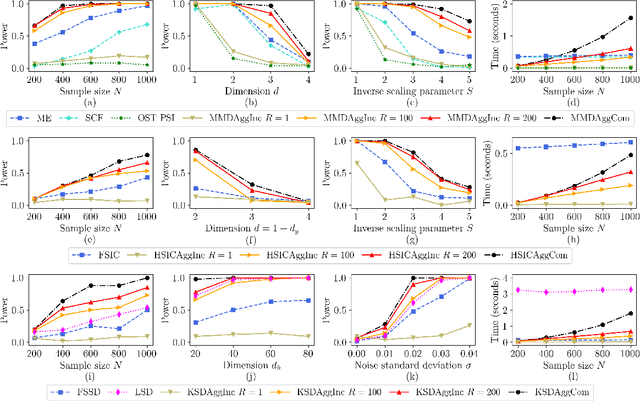
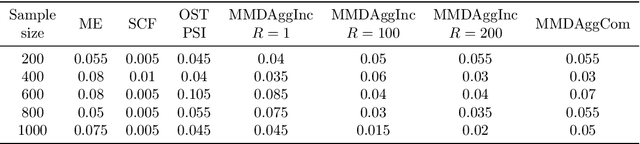
We propose a series of computationally efficient, nonparametric tests for the two-sample, independence and goodness-of-fit problems, using the Maximum Mean Discrepancy (MMD), Hilbert Schmidt Independence Criterion (HSIC), and Kernel Stein Discrepancy (KSD), respectively. Our test statistics are incomplete $U$-statistics, with a computational cost that interpolates between linear time in the number of samples, and quadratic time, as associated with classical $U$-statistic tests. The three proposed tests aggregate over several kernel bandwidths to detect departures from the null on various scales: we call the resulting tests MMDAggInc, HSICAggInc and KSDAggInc. For the test thresholds, we derive a quantile bound for wild bootstrapped incomplete $U$- statistics, which is of independent interest. We derive uniform separation rates for MMDAggInc and HSICAggInc, and quantify exactly the trade-off between computational efficiency and the attainable rates: this result is novel for tests based on incomplete $U$-statistics, to our knowledge. We further show that in the quadratic-time case, the wild bootstrap incurs no penalty to test power over more widespread permutation-based approaches, since both attain the same minimax optimal rates (which in turn match the rates that use oracle quantiles). We support our claims with numerical experiments on the trade-off between computational efficiency and test power. In the three testing frameworks, we observe that our proposed linear-time aggregated tests obtain higher power than current state-of-the-art linear-time kernel tests.

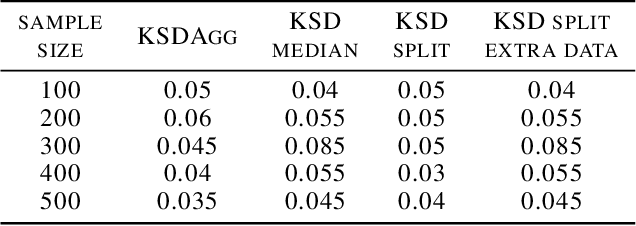
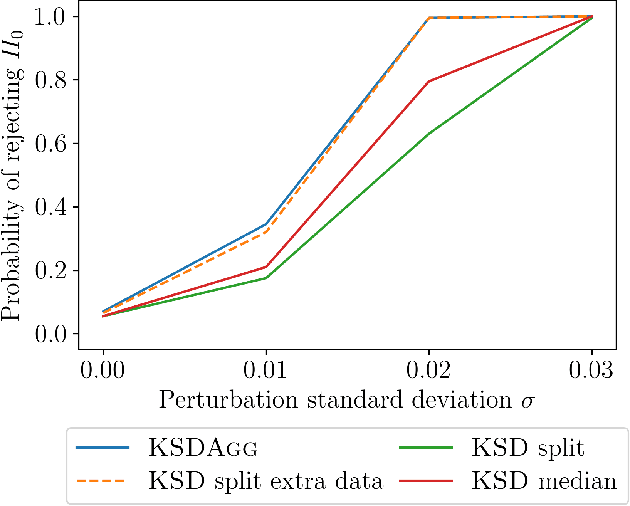
KSD Aggregated Goodness-of-fit Test

We investigate properties of goodness-of-fit tests based on the Kernel Stein Discrepancy (KSD). We introduce a strategy to construct a test, called KSDAgg, which aggregates multiple tests with different kernels. KSDAgg avoids splitting the data to perform kernel selection (which leads to a loss in test power), and rather maximises the test power over a collection of kernels. We provide theoretical guarantees on the power of KSDAgg: we show it achieves the smallest uniform separation rate of the collection, up to a logarithmic term. KSDAgg can be computed exactly in practice as it relies either on a parametric bootstrap or on a wild bootstrap to estimate the quantiles and the level corrections. In particular, for the crucial choice of bandwidth of a fixed kernel, it avoids resorting to arbitrary heuristics (such as median or standard deviation) or to data splitting. We find on both synthetic and real-world data that KSDAgg outperforms other state-of-the-art adaptive KSD-based goodness-of-fit testing procedures.