A Multivariate Extreme Value Theory Approach to Anomaly Clustering and Visualization

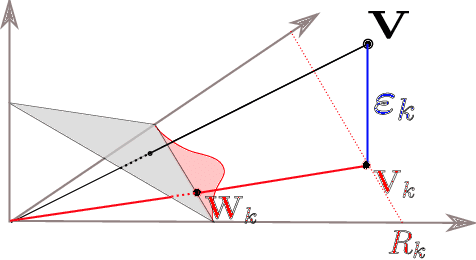
In a wide variety of situations, anomalies in the behaviour of a complex system, whose health is monitored through the observation of a random vector X = (X1,. .. , X d) valued in R d , correspond to the simultaneous occurrence of extreme values for certain subgroups $\alpha$ $\subset$ {1,. .. , d} of variables Xj. Under the heavy-tail assumption, which is precisely appropriate for modeling these phenomena, statistical methods relying on multivariate extreme value theory have been developed in the past few years for identifying such events/subgroups. This paper exploits this approach much further by means of a novel mixture model that permits to describe the distribution of extremal observations and where the anomaly type $\alpha$ is viewed as a latent variable. One may then take advantage of the model by assigning to any extreme point a posterior probability for each anomaly type $\alpha$, defining implicitly a similarity measure between anomalies. It is explained at length how the latter permits to cluster extreme observations and obtain an informative planar representation of anomalies using standard graph-mining tools. The relevance and usefulness of the clustering and 2-d visual display thus designed is illustrated on simulated datasets and on real observations as well, in the aeronautics application domain.

One Class Splitting Criteria for Random Forests

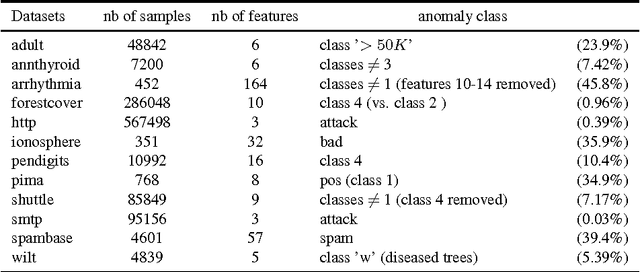
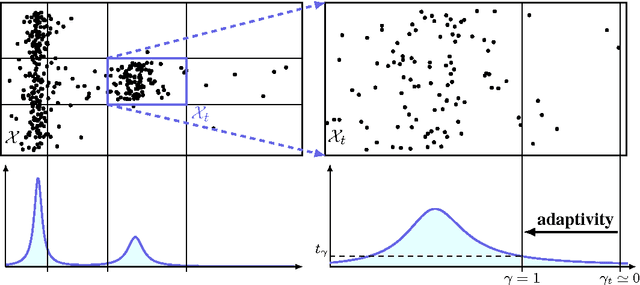
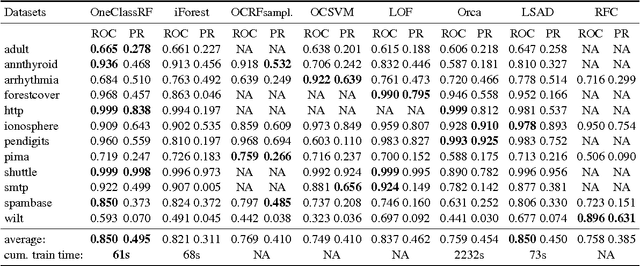
Random Forests (RFs) are strong machine learning tools for classification and regression. However, they remain supervised algorithms, and no extension of RFs to the one-class setting has been proposed, except for techniques based on second-class sampling. This work fills this gap by proposing a natural methodology to extend standard splitting criteria to the one-class setting, structurally generalizing RFs to one-class classification. An extensive benchmark of seven state-of-the-art anomaly detection algorithms is also presented. This empirically demonstrates the relevance of our approach.