On the Dualization of Operator-Valued Kernel Machines
Paper and Code
Oct 10, 2019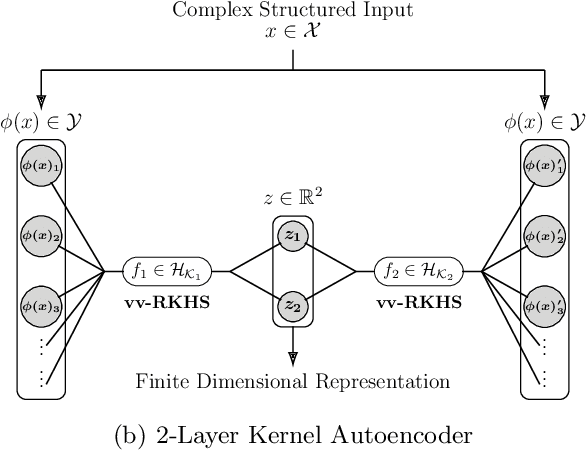
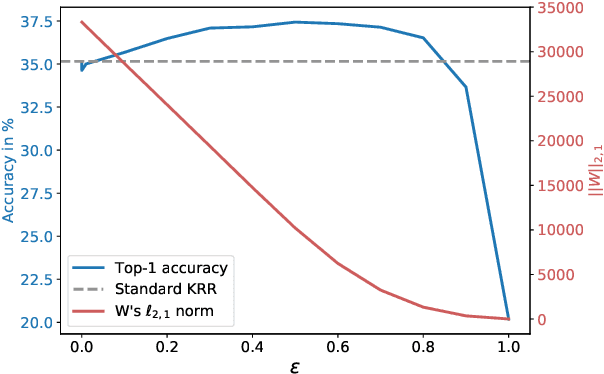
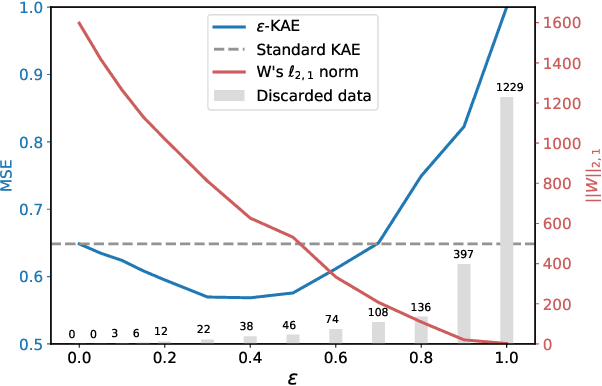
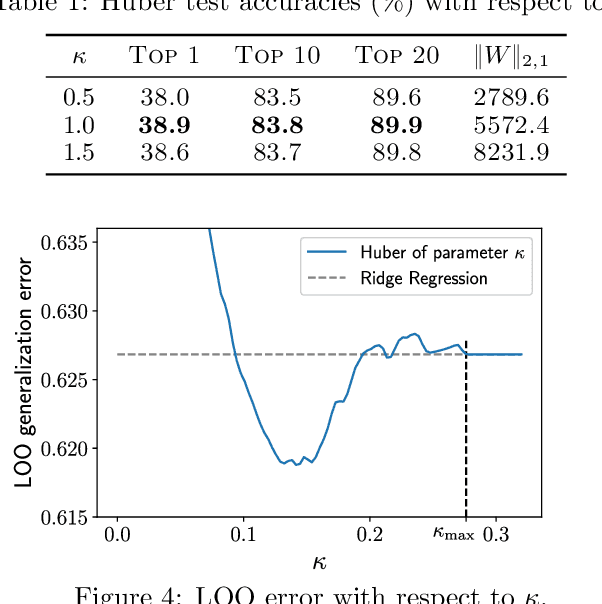
Operator-Valued Kernels (OVKs) and Vector-Valued Reproducing Kernel Hilbert Spaces (vv-RKHSs) provide an elegant way to extend scalar kernel methods when the output space is a Hilbert space. First used in multi-task regression, this theoretical framework opens the door to various applications, ranging from structured output prediction to functional regression, thanks to its ability to deal with infinite dimensional output spaces. This work investigates how to use the duality principle to handle different families of loss functions, yet unexplored within vv-RKHSs. The difficulty of having infinite dimensional dual variables is overcome, either by means of a Double Representer Theorem when the loss depends on inner products solely, or by an in-depth analysis of the Fenchel-Legendre transform of integral losses. Experiments on structured prediction, function-to-function regression and structured representation learning with $\epsilon$-insensitive and Huber losses illustrate the benefits of this framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge