MMTEB: Massive Multilingual Text Embedding Benchmark

Text embeddings are typically evaluated on a limited set of tasks, which are constrained by language, domain, and task diversity. To address these limitations and provide a more comprehensive evaluation, we introduce the Massive Multilingual Text Embedding Benchmark (MMTEB) - a large-scale, community-driven expansion of MTEB, covering over 500 quality-controlled evaluation tasks across 250+ languages. MMTEB includes a diverse set of challenging, novel tasks such as instruction following, long-document retrieval, and code retrieval, representing the largest multilingual collection of evaluation tasks for embedding models to date. Using this collection, we develop several highly multilingual benchmarks, which we use to evaluate a representative set of models. We find that while large language models (LLMs) with billions of parameters can achieve state-of-the-art performance on certain language subsets and task categories, the best-performing publicly available model is multilingual-e5-large-instruct with only 560 million parameters. To facilitate accessibility and reduce computational cost, we introduce a novel downsampling method based on inter-task correlation, ensuring a diverse selection while preserving relative model rankings. Furthermore, we optimize tasks such as retrieval by sampling hard negatives, creating smaller but effective splits. These optimizations allow us to introduce benchmarks that drastically reduce computational demands. For instance, our newly introduced zero-shot English benchmark maintains a ranking order similar to the full-scale version but at a fraction of the computational cost.

Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

MASAI: Modular Architecture for Software-engineering AI Agents

A common method to solve complex problems in software engineering, is to divide the problem into multiple sub-problems. Inspired by this, we propose a Modular Architecture for Software-engineering AI (MASAI) agents, where different LLM-powered sub-agents are instantiated with well-defined objectives and strategies tuned to achieve those objectives. Our modular architecture offers several advantages: (1) employing and tuning different problem-solving strategies across sub-agents, (2) enabling sub-agents to gather information from different sources scattered throughout a repository, and (3) avoiding unnecessarily long trajectories which inflate costs and add extraneous context. MASAI enabled us to achieve the highest performance (28.33% resolution rate) on the popular and highly challenging SWE-bench Lite dataset consisting of 300 GitHub issues from 11 Python repositories. We conduct a comprehensive evaluation of MASAI relative to other agentic methods and analyze the effects of our design decisions and their contribution to the success of MASAI.

Language Agnostic Code Embeddings

Recently, code language models have achieved notable advancements in addressing a diverse array of essential code comprehension and generation tasks. Yet, the field lacks a comprehensive deep dive and understanding of the code embeddings of multilingual code models. In this paper, we present a comprehensive study on multilingual code embeddings, focusing on the cross-lingual capabilities of these embeddings across different programming languages. Through probing experiments, we demonstrate that code embeddings comprise two distinct components: one deeply tied to the nuances and syntax of a specific language, and the other remaining agnostic to these details, primarily focusing on semantics. Further, we show that when we isolate and eliminate this language-specific component, we witness significant improvements in downstream code retrieval tasks, leading to an absolute increase of up to +17 in the Mean Reciprocal Rank (MRR).

Locally Differentially Private Document Generation Using Zero Shot Prompting

Numerous studies have highlighted the privacy risks associated with pretrained large language models. In contrast, our research offers a unique perspective by demonstrating that pretrained large language models can effectively contribute to privacy preservation. We propose a locally differentially private mechanism called DP-Prompt, which leverages the power of pretrained large language models and zero-shot prompting to counter author de-anonymization attacks while minimizing the impact on downstream utility. When DP-Prompt is used with a powerful language model like ChatGPT (gpt-3.5), we observe a notable reduction in the success rate of de-anonymization attacks, showing that it surpasses existing approaches by a considerable margin despite its simpler design. For instance, in the case of the IMDB dataset, DP-Prompt (with ChatGPT) perfectly recovers the clean sentiment F1 score while achieving a 46\% reduction in author identification F1 score against static attackers and a 26\% reduction against adaptive attackers. We conduct extensive experiments across six open-source large language models, ranging up to 7 billion parameters, to analyze various effects of the privacy-utility tradeoff.

Rieoptax: Riemannian Optimization in JAX

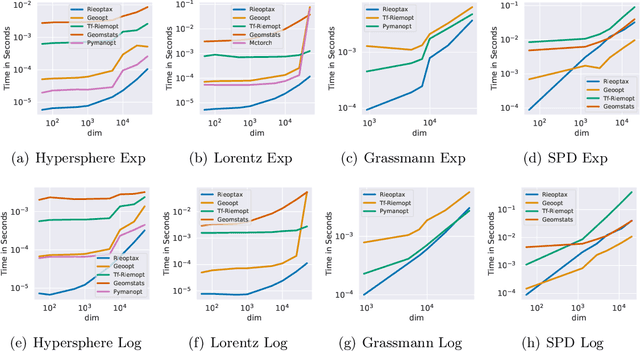
We present Rieoptax, an open source Python library for Riemannian optimization in JAX. We show that many differential geometric primitives, such as Riemannian exponential and logarithm maps, are usually faster in Rieoptax than existing frameworks in Python, both on CPU and GPU. We support various range of basic and advanced stochastic optimization solvers like Riemannian stochastic gradient, stochastic variance reduction, and adaptive gradient methods. A distinguishing feature of the proposed toolbox is that we also support differentially private optimization on Riemannian manifolds.

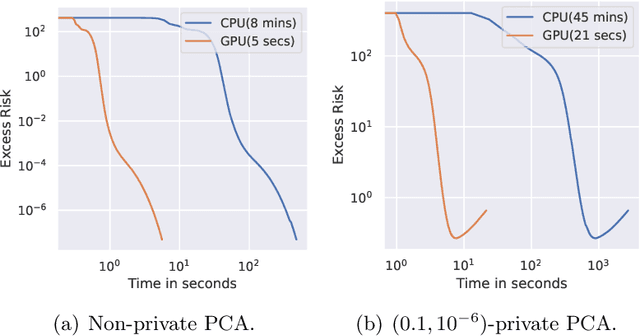
Differentially Private Fréchet Mean on the Manifold of Symmetric Positive Definite (SPD) Matrices

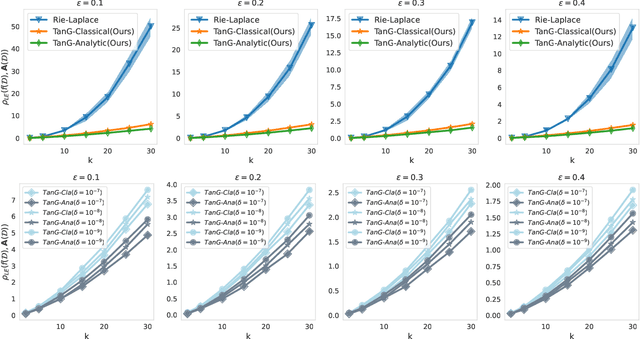
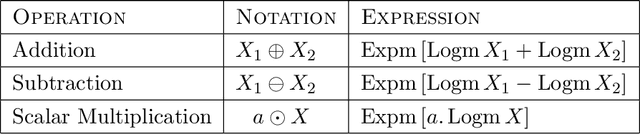
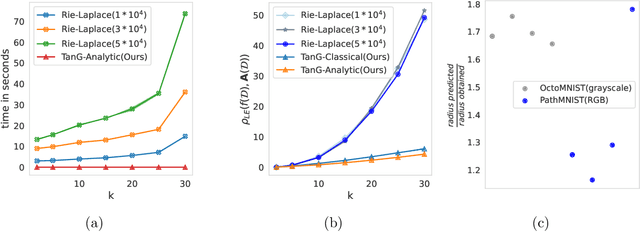
Differential privacy has become crucial in the real-world deployment of statistical and machine learning algorithms with rigorous privacy guarantees. The earliest statistical queries, for which differential privacy mechanisms have been developed, were for the release of the sample mean. In Geometric Statistics, the sample Fr\'echet mean represents one of the most fundamental statistical summaries, as it generalizes the sample mean for data belonging to nonlinear manifolds. In that spirit, the only geometric statistical query for which a differential privacy mechanism has been developed, so far, is for the release of the sample Fr\'echet mean: the \emph{Riemannian Laplace mechanism} was recently proposed to privatize the Fr\'echet mean on complete Riemannian manifolds. In many fields, the manifold of Symmetric Positive Definite (SPD) matrices is used to model data spaces, including in medical imaging where privacy requirements are key. We propose a novel, simple and fast mechanism - the \emph{Tangent Gaussian mechanism} - to compute a differentially private Fr\'echet mean on the SPD manifold endowed with the log-Euclidean Riemannian metric. We show that our new mechanism obtains quadratic utility improvement in terms of data dimension over the current and only available baseline. Our mechanism is also simpler in practice as it does not require any expensive Markov Chain Monte Carlo (MCMC) sampling, and is computationally faster by multiple orders of magnitude -- as confirmed by extensive experiments.

Shrinkage Estimation of Higher Order Bochner Integrals

We consider shrinkage estimation of higher order Hilbert space valued Bochner integrals in a non-parametric setting. We propose estimators that shrink the $U$-statistic estimator of the Bochner integral towards a pre-specified target element in the Hilbert space. Depending on the degeneracy of the kernel of the $U$-statistic, we construct consistent shrinkage estimators with fast rates of convergence, and develop oracle inequalities comparing the risks of the the $U$-statistic estimator and its shrinkage version. Surprisingly, we show that the shrinkage estimator designed by assuming complete degeneracy of the kernel of the $U$-statistic is a consistent estimator even when the kernel is not complete degenerate. This work subsumes and improves upon Krikamol et al., 2016, JMLR and Zhou et al., 2019, JMVA, which only handle mean element and covariance operator estimation in a reproducing kernel Hilbert space. We also specialize our results to normal mean estimation and show that for $d\ge 3$, the proposed estimator strictly improves upon the sample mean in terms of the mean squared error.

Quantile Regularization: Towards Implicit Calibration of Regression Models

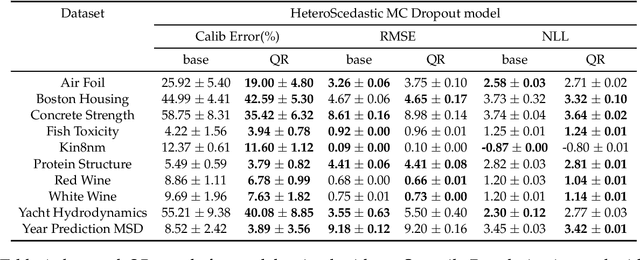
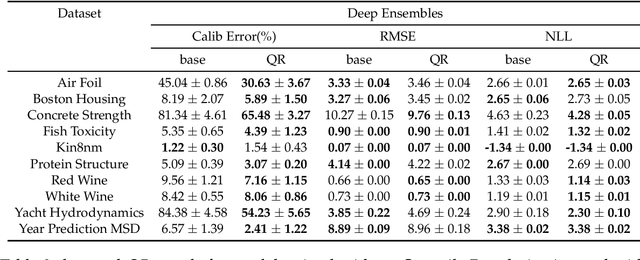
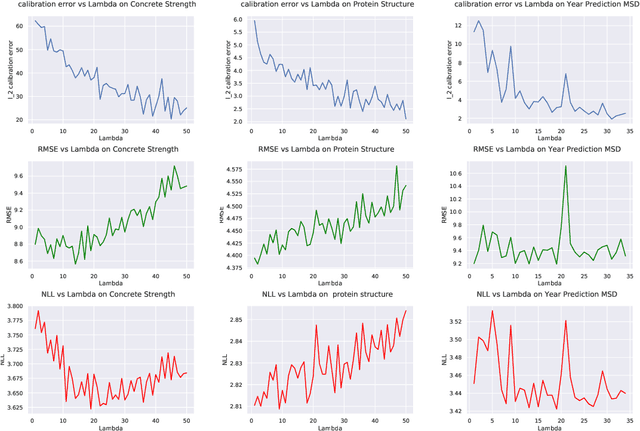
Recent works have shown that most deep learning models are often poorly calibrated, i.e., they may produce overconfident predictions that are wrong. It is therefore desirable to have models that produce predictive uncertainty estimates that are reliable. Several approaches have been proposed recently to calibrate classification models. However, there is relatively little work on calibrating regression models. We present a method for calibrating regression models based on a novel quantile regularizer defined as the cumulative KL divergence between two CDFs. Unlike most of the existing approaches for calibrating regression models, which are based on post-hoc processing of the model's output and require an additional dataset, our method is trainable in an end-to-end fashion without requiring an additional dataset. The proposed regularizer can be used with any training objective for regression. We also show that post-hoc calibration methods like Isotonic Calibration sometimes compound miscalibration whereas our method provides consistently better calibrations. We provide empirical results demonstrating that the proposed quantile regularizer significantly improves calibration for regression models trained using approaches, such as Dropout VI and Deep Ensembles.