Differentially Private Fréchet Mean on the Manifold of Symmetric Positive Definite (SPD) Matrices

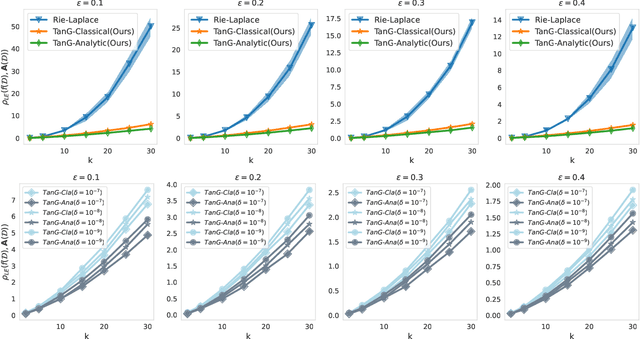
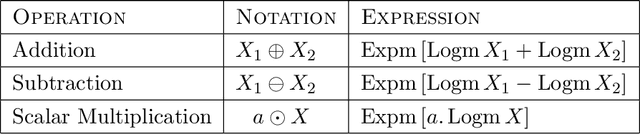
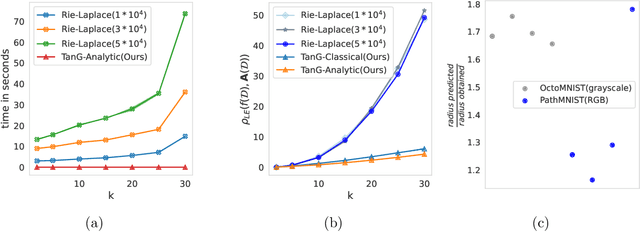
Differential privacy has become crucial in the real-world deployment of statistical and machine learning algorithms with rigorous privacy guarantees. The earliest statistical queries, for which differential privacy mechanisms have been developed, were for the release of the sample mean. In Geometric Statistics, the sample Fr\'echet mean represents one of the most fundamental statistical summaries, as it generalizes the sample mean for data belonging to nonlinear manifolds. In that spirit, the only geometric statistical query for which a differential privacy mechanism has been developed, so far, is for the release of the sample Fr\'echet mean: the \emph{Riemannian Laplace mechanism} was recently proposed to privatize the Fr\'echet mean on complete Riemannian manifolds. In many fields, the manifold of Symmetric Positive Definite (SPD) matrices is used to model data spaces, including in medical imaging where privacy requirements are key. We propose a novel, simple and fast mechanism - the \emph{Tangent Gaussian mechanism} - to compute a differentially private Fr\'echet mean on the SPD manifold endowed with the log-Euclidean Riemannian metric. We show that our new mechanism obtains quadratic utility improvement in terms of data dimension over the current and only available baseline. Our mechanism is also simpler in practice as it does not require any expensive Markov Chain Monte Carlo (MCMC) sampling, and is computationally faster by multiple orders of magnitude -- as confirmed by extensive experiments.