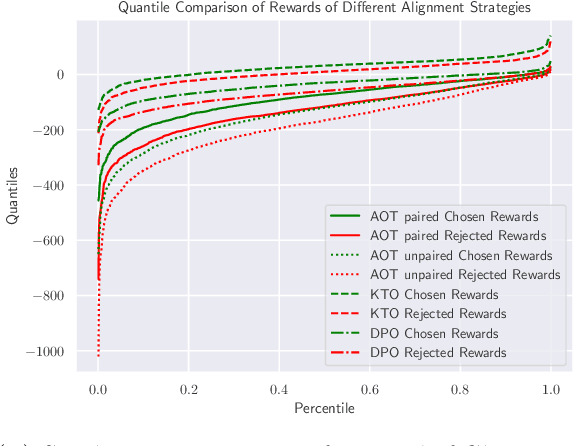
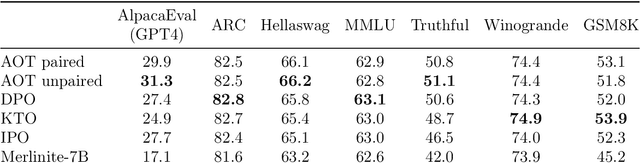
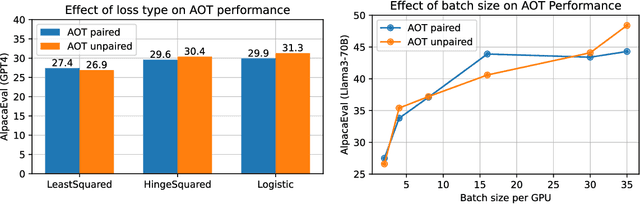
Distributional Preference Alignment of LLMs via Optimal Transport

Current LLM alignment techniques use pairwise human preferences at a sample level, and as such, they do not imply an alignment on the distributional level. We propose in this paper Alignment via Optimal Transport (AOT), a novel method for distributional preference alignment of LLMs. AOT aligns LLMs on unpaired preference data by making the reward distribution of the positive samples stochastically dominant in the first order on the distribution of negative samples. We introduce a convex relaxation of this first-order stochastic dominance and cast it as an optimal transport problem with a smooth and convex cost. Thanks to the one-dimensional nature of the resulting optimal transport problem and the convexity of the cost, it has a closed-form solution via sorting on empirical measures. We fine-tune LLMs with this AOT objective, which enables alignment by penalizing the violation of the stochastic dominance of the reward distribution of the positive samples on the reward distribution of the negative samples. We analyze the sample complexity of AOT by considering the dual of the OT problem and show that it converges at the parametric rate. Empirically, we show on a diverse set of alignment datasets and LLMs that AOT leads to state-of-the-art models in the 7B family of models when evaluated with Open LLM Benchmarks and AlpacaEval.

Risk Assessment and Statistical Significance in the Age of Foundation Models

We propose a distributional framework for assessing socio-technical risks of foundation models with quantified statistical significance. Our approach hinges on a new statistical relative testing based on first and second order stochastic dominance of real random variables. We show that the second order statistics in this test are linked to mean-risk models commonly used in econometrics and mathematical finance to balance risk and utility when choosing between alternatives. Using this framework, we formally develop a risk-aware approach for foundation model selection given guardrails quantified by specified metrics. Inspired by portfolio optimization and selection theory in mathematical finance, we define a \emph{metrics portfolio} for each model as a means to aggregate a collection of metrics, and perform model selection based on the stochastic dominance of these portfolios. The statistical significance of our tests is backed theoretically by an asymptotic analysis via central limit theorems instantiated in practice via a bootstrap variance estimate. We use our framework to compare various large language models regarding risks related to drifting from instructions and outputting toxic content.

Auditing and Generating Synthetic Data with Controllable Trust Trade-offs

Data collected from the real world tends to be biased, unbalanced, and at risk of exposing sensitive and private information. This reality has given rise to the idea of creating synthetic datasets to alleviate risk, bias, harm, and privacy concerns inherent in the real data. This concept relies on Generative AI models to produce unbiased, privacy-preserving synthetic data while being true to the real data. In this new paradigm, how can we tell if this approach delivers on its promises? We present an auditing framework that offers a holistic assessment of synthetic datasets and AI models trained on them, centered around bias and discrimination prevention, fidelity to the real data, utility, robustness, and privacy preservation. We showcase our framework by auditing multiple generative models on diverse use cases, including education, healthcare, banking, human resources, and across different modalities, from tabular, to time-series, to natural language. Our use cases demonstrate the importance of a holistic assessment in order to ensure compliance with socio-technical safeguards that regulators and policymakers are increasingly enforcing. For this purpose, we introduce the trust index that ranks multiple synthetic datasets based on their prescribed safeguards and their desired trade-offs. Moreover, we devise a trust-index-driven model selection and cross-validation procedure via auditing in the training loop that we showcase on a class of transformer models that we dub TrustFormers, across different modalities. This trust-driven model selection allows for controllable trust trade-offs in the resulting synthetic data. We instrument our auditing framework with workflows that connect different stakeholders from model development to audit and certification via a synthetic data auditing report.

Do Large Scale Molecular Language Representations Capture Important Structural Information?

Predicting chemical properties from the structure of a molecule is of great importance in many applications including drug discovery and material design. Machine learning based molecular property prediction holds the promise of enabling accurate predictions at much less complexity, when compared to, for example Density Functional Theory (DFT) calculations. Features extracted from molecular graphs, using graph neural nets in a supervised manner, have emerged as strong baselines for such tasks. However, the vast chemical space together with the limited availability of labels makes supervised learning challenging, calling for learning a general-purpose molecular representation. Recently, pre-trained transformer-based language models (PTLMs) on large unlabeled corpus have produced state-of-the-art results in many downstream natural language processing tasks. Inspired by this development, here we present molecular embeddings obtained by training an efficient transformer encoder model, referred to as MoLFormer. This model was employed with a linear attention mechanism and highly paralleized training on 1D SMILES sequences of 1.1 billion unlabeled molecules from the PubChem and ZINC datasets. Experiments show that the learned molecular representation performs competitively, when compared to existing graph-based and fingerprint-based supervised learning baselines, on the challenging tasks of predicting properties of QM8 and QM9 molecules. Further task-specific fine-tuning of the MoLFormerr representation improves performance on several of those property prediction benchmarks. These results provide encouraging evidence that large-scale molecular language models can capture sufficient structural information to be able to accurately predict quantum chemical properties and beyond.

Tabular Transformers for Modeling Multivariate Time Series

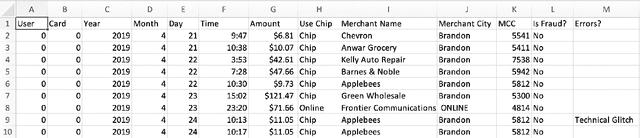
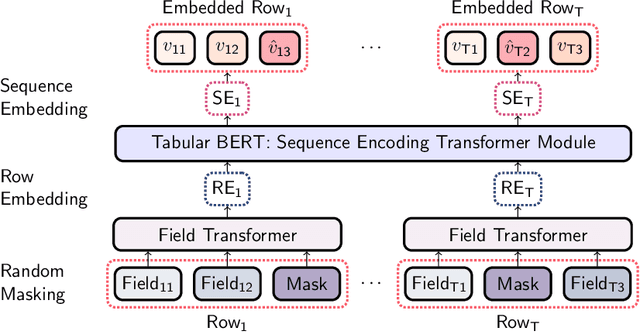
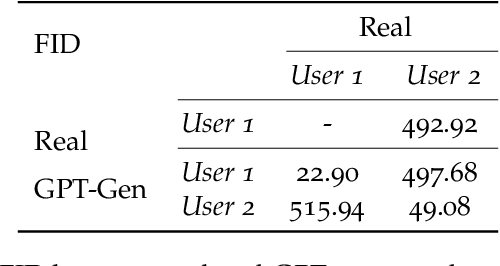
Tabular datasets are ubiquitous in data science applications. Given their importance, it seems natural to apply state-of-the-art deep learning algorithms in order to fully unlock their potential. Here we propose neural network models that represent tabular time series that can optionally leverage their hierarchical structure. This results in two architectures for tabular time series: one for learning representations that is analogous to BERT and can be pre-trained end-to-end and used in downstream tasks, and one that is akin to GPT and can be used for generation of realistic synthetic tabular sequences. We demonstrate our models on two datasets: a synthetic credit card transaction dataset, where the learned representations are used for fraud detection and synthetic data generation, and on a real pollution dataset, where the learned encodings are used to predict atmospheric pollutant concentrations. Code and data are available at https://github.com/IBM/TabFormer.

Fast Mixing of Multi-Scale Langevin Dynamics under the Manifold Hypothesis

Recently, the task of image generation has attracted much attention. In particular, the recent empirical successes of the Markov Chain Monte Carlo (MCMC) technique of Langevin Dynamics have prompted a number of theoretical advances; despite this, several outstanding problems remain. First, the Langevin Dynamics is run in very high dimension on a nonconvex landscape; in the worst case, due to the NP-hardness of nonconvex optimization, it is thought that Langevin Dynamics mixes only in time exponential in the dimension. In this work, we demonstrate how the manifold hypothesis allows for the considerable reduction of mixing time, from exponential in the ambient dimension to depending only on the (much smaller) intrinsic dimension of the data. Second, the high dimension of the sampling space significantly hurts the performance of Langevin Dynamics; we leverage a multi-scale approach to help ameliorate this issue and observe that this multi-resolution algorithm allows for a trade-off between image quality and computational expense in generation.

Towards Better Understanding of Adaptive Gradient Algorithms in Generative Adversarial Nets

Adaptive gradient algorithms perform gradient-based updates using the history of gradients and are ubiquitous in training deep neural networks. While adaptive gradient methods theory is well understood for minimization problems, the underlying factors driving their empirical success in min-max problems such as GANs remain unclear. In this paper, we aim at bridging this gap from both theoretical and empirical perspectives. First, we analyze a variant of Optimistic Stochastic Gradient (OSG) proposed in~\citep{daskalakis2017training} for solving a class of non-convex non-concave min-max problem and establish $O(\epsilon^{-4})$ complexity for finding $\epsilon$-first-order stationary point, in which the algorithm only requires invoking one stochastic first-order oracle while enjoying state-of-the-art iteration complexity achieved by stochastic extragradient method by~\citep{iusem2017extragradient}. Then we propose an adaptive variant of OSG named Optimistic Adagrad (OAdagrad) and reveal an \emph{improved} adaptive complexity $\widetilde{O}\left(\epsilon^{-\frac{2}{1-\alpha}}\right)$~\footnote{Here $\widetilde{O}(\cdot)$ compresses a logarithmic factor of $\epsilon$.}, where $\alpha$ characterizes the growth rate of the cumulative stochastic gradient and $0\leq \alpha\leq 1/2$. To the best of our knowledge, this is the first work for establishing adaptive complexity in non-convex non-concave min-max optimization. Empirically, our experiments show that indeed adaptive gradient algorithms outperform their non-adaptive counterparts in GAN training. Moreover, this observation can be explained by the slow growth rate of the cumulative stochastic gradient, as observed empirically.

Decentralized Parallel Algorithm for Training Generative Adversarial Nets

Generative Adversarial Networks (GANs) are powerful class of generative models in the deep learning community. Current practice on large-scale GAN training \cite{brock2018large} utilizes large models and distributed large-batch training strategies, and is implemented on deep learning frameworks (e.g., TensorFlow, PyTorch, etc.) designed in a centralized manner. In the centralized network topology, every worker needs to communicate with the central node. However, when the network bandwidth is low or network latency is high, the performance would be significantly degraded. Despite recent progress on decentralized algorithms for training deep neural networks, it remains unclear whether it is possible to train GANs in a decentralized manner. In this paper, we design a decentralized algorithm for solving a class of non-convex non-concave min-max problem with provable guarantee. Experimental results on GANs demonstrate the effectiveness of the proposed algorithm.

Wasserstein Barycenter Model Ensembling

In this paper we propose to perform model ensembling in a multiclass or a multilabel learning setting using Wasserstein (W.) barycenters. Optimal transport metrics, such as the Wasserstein distance, allow incorporating semantic side information such as word embeddings. Using W. barycenters to find the consensus between models allows us to balance confidence and semantics in finding the agreement between the models. We show applications of Wasserstein ensembling in attribute-based classification, multilabel learning and image captioning generation. These results show that the W. ensembling is a viable alternative to the basic geometric or arithmetic mean ensembling.