Neural Spacetimes for DAG Representation Learning
Paper and Code
Aug 25, 2024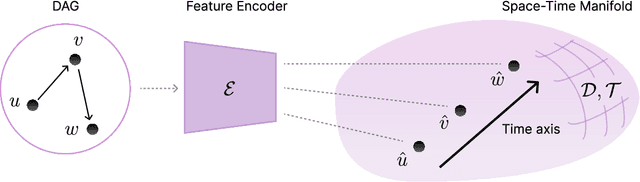
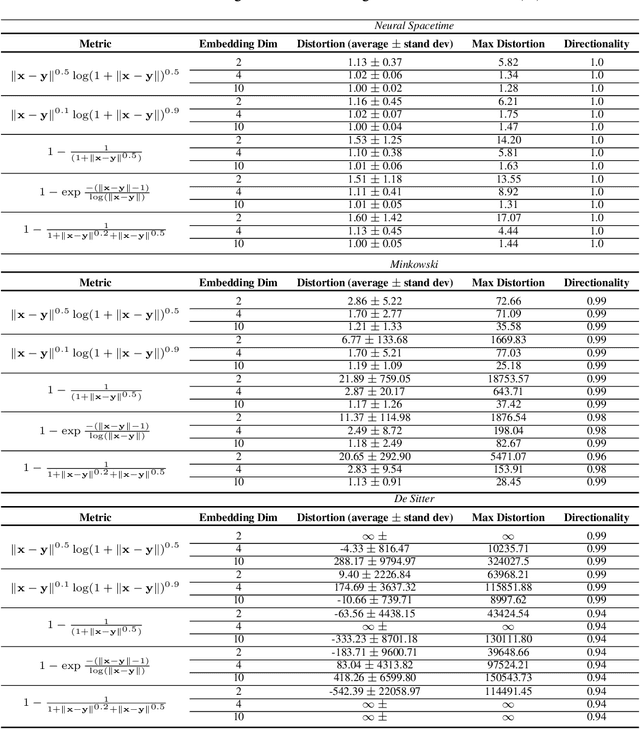
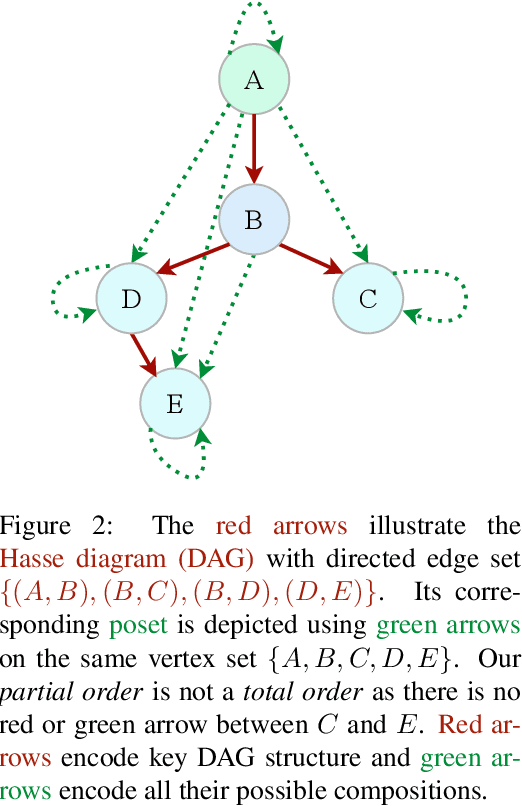
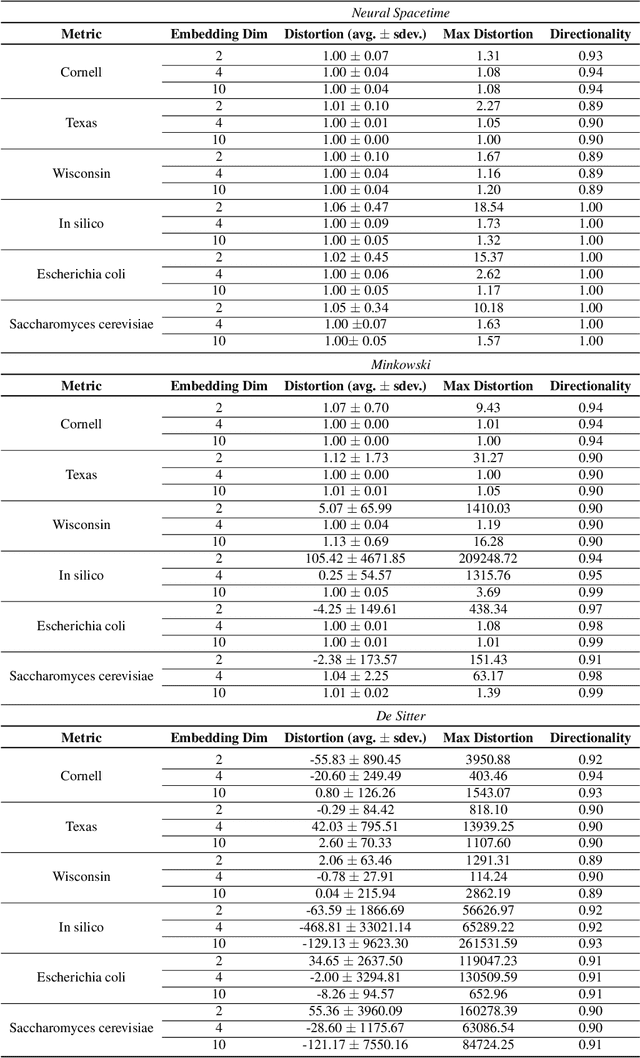
We propose a class of trainable deep learning-based geometries called Neural Spacetimes (NSTs), which can universally represent nodes in weighted directed acyclic graphs (DAGs) as events in a spacetime manifold. While most works in the literature focus on undirected graph representation learning or causality embedding separately, our differentiable geometry can encode both graph edge weights in its spatial dimensions and causality in the form of edge directionality in its temporal dimensions. We use a product manifold that combines a quasi-metric (for space) and a partial order (for time). NSTs are implemented as three neural networks trained in an end-to-end manner: an embedding network, which learns to optimize the location of nodes as events in the spacetime manifold, and two other networks that optimize the space and time geometries in parallel, which we call a neural (quasi-)metric and a neural partial order, respectively. The latter two networks leverage recent ideas at the intersection of fractal geometry and deep learning to shape the geometry of the representation space in a data-driven fashion, unlike other works in the literature that use fixed spacetime manifolds such as Minkowski space or De Sitter space to embed DAGs. Our main theoretical guarantee is a universal embedding theorem, showing that any $k$-point DAG can be embedded into an NST with $1+\mathcal{O}(\log(k))$ distortion while exactly preserving its causal structure. The total number of parameters defining the NST is sub-cubic in $k$ and linear in the width of the DAG. If the DAG has a planar Hasse diagram, this is improved to $\mathcal{O}(\log(k)) + 2)$ spatial and 2 temporal dimensions. We validate our framework computationally with synthetic weighted DAGs and real-world network embeddings; in both cases, the NSTs achieve lower embedding distortions than their counterparts using fixed spacetime geometries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge