Slicing Mutual Information Generalization Bounds for Neural Networks

The ability of machine learning (ML) algorithms to generalize well to unseen data has been studied through the lens of information theory, by bounding the generalization error with the input-output mutual information (MI), i.e., the MI between the training data and the learned hypothesis. Yet, these bounds have limited practicality for modern ML applications (e.g., deep learning), due to the difficulty of evaluating MI in high dimensions. Motivated by recent findings on the compressibility of neural networks, we consider algorithms that operate by slicing the parameter space, i.e., trained on random lower-dimensional subspaces. We introduce new, tighter information-theoretic generalization bounds tailored for such algorithms, demonstrating that slicing improves generalization. Our bounds offer significant computational and statistical advantages over standard MI bounds, as they rely on scalable alternative measures of dependence, i.e., disintegrated mutual information and $k$-sliced mutual information. Then, we extend our analysis to algorithms whose parameters do not need to exactly lie on random subspaces, by leveraging rate-distortion theory. This strategy yields generalization bounds that incorporate a distortion term measuring model compressibility under slicing, thereby tightening existing bounds without compromising performance or requiring model compression. Building on this, we propose a regularization scheme enabling practitioners to control generalization through compressibility. Finally, we empirically validate our results and achieve the computation of non-vacuous information-theoretic generalization bounds for neural networks, a task that was previously out of reach.

Asymmetry in Low-Rank Adapters of Foundation Models

Parameter-efficient fine-tuning optimizes large, pre-trained foundation models by updating a subset of parameters; in this class, Low-Rank Adaptation (LoRA) is particularly effective. Inspired by an effort to investigate the different roles of LoRA matrices during fine-tuning, this paper characterizes and leverages unexpected asymmetry in the importance of low-rank adapter matrices. Specifically, when updating the parameter matrices of a neural network by adding a product $BA$, we observe that the $B$ and $A$ matrices have distinct functions: $A$ extracts features from the input, while $B$ uses these features to create the desired output. Based on this observation, we demonstrate that fine-tuning $B$ is inherently more effective than fine-tuning $A$, and that a random untrained $A$ should perform nearly as well as a fine-tuned one. Using an information-theoretic lens, we also bound the generalization of low-rank adapters, showing that the parameter savings of exclusively training $B$ improves the bound. We support our conclusions with experiments on RoBERTa, BART-Large, LLaMA-2, and ViTs.

Topological Approaches to Deep Learning

We perform topological data analysis on the internal states of convolutional deep neural networks to develop an understanding of the computations that they perform. We apply this understanding to modify the computations so as to (a) speed up computations and (b) improve generalization from one data set of digits to another. One byproduct of the analysis is the production of a geometry on new sets of features on data sets of images, and use this observation to develop a methodology for constructing analogues of CNN's for many other geometries, including the graph structures constructed by topological data analysis.

A look at the topology of convolutional neural networks

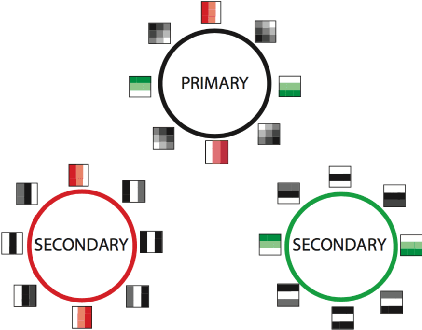
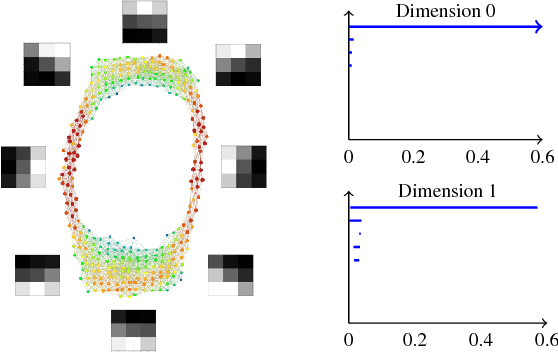
Convolutional neural networks (CNN's) are powerful and widely used tools. However, their interpretability is far from ideal. In this paper we use topological data analysis to investigate what various CNN's learn. We show that the weights of convolutional layers at depths from 1 through 13 learn simple global structures. We also demonstrate the change of the simple structures over the course of training. In particular, we define and analyze the spaces of spatial filters of convolutional layers and show the recurrence, among all networks, depths, and during training, of a simple circle consisting of rotating edges, as well as a less recurring unanticipated complex circle that combines lines, edges, and non-linear patterns. We train over a thousand CNN's on MNIST and CIFAR-10, as well as use VGG-networks pretrained on ImageNet.