A look at the topology of convolutional neural networks

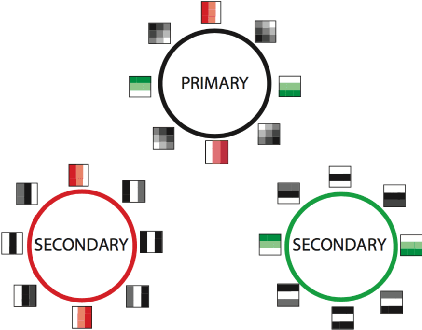
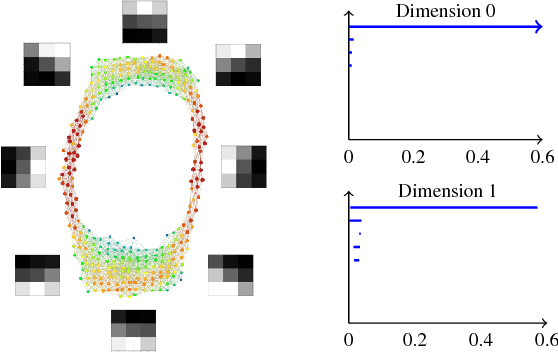
Convolutional neural networks (CNN's) are powerful and widely used tools. However, their interpretability is far from ideal. In this paper we use topological data analysis to investigate what various CNN's learn. We show that the weights of convolutional layers at depths from 1 through 13 learn simple global structures. We also demonstrate the change of the simple structures over the course of training. In particular, we define and analyze the spaces of spatial filters of convolutional layers and show the recurrence, among all networks, depths, and during training, of a simple circle consisting of rotating edges, as well as a less recurring unanticipated complex circle that combines lines, edges, and non-linear patterns. We train over a thousand CNN's on MNIST and CIFAR-10, as well as use VGG-networks pretrained on ImageNet.