Truly Mesh-free Physics-Informed Neural Networks

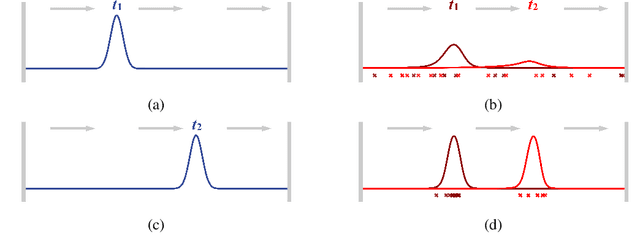
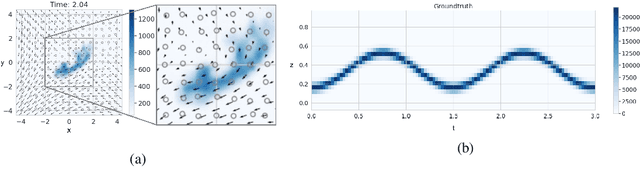
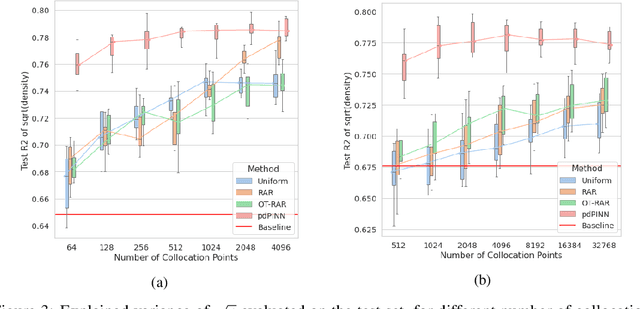
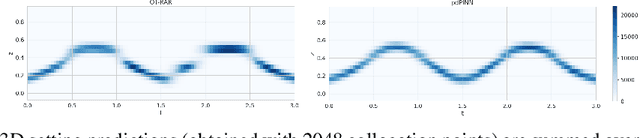
Physics-informed Neural Networks (PINNs) have recently emerged as a principled way to include prior physical knowledge in form of partial differential equations (PDEs) into neural networks. Although generally viewed as being mesh-free, current approaches still rely on collocation points obtained within a bounded region, even in settings with spatially sparse signals. Furthermore, if the boundaries are not known, the selection of such a region may be arbitrary, resulting in a large proportion of collocation points being selected in areas of low relevance. To resolve this, we present a mesh-free and adaptive approach termed particle-density PINN (pdPINN), which is inspired by the microscopic viewpoint of fluid dynamics. Instead of sampling from a bounded region, we propose to sample directly from the distribution over the (fluids) particle positions, eliminating the need to introduce boundaries while adaptively focusing on the most relevant regions. This is achieved by reformulating the modeled fluid density as an unnormalized probability distribution from which we sample with dynamic Monte Carlo methods. We further generalize pdPINNs to different settings that allow interpreting a positive scalar quantity as a particle density, such as the evolution of the temperature in the heat equation. The utility of our approach is demonstrated on experiments for modeling (non-steady) compressible fluids in up to three dimensions and a two-dimensional diffusion problem, illustrating the high flexibility and sample efficiency compared to existing refinement methods for PINNs.

Learning Invariances with Generalised Input-Convex Neural Networks

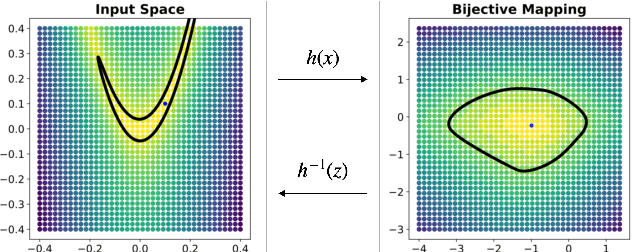
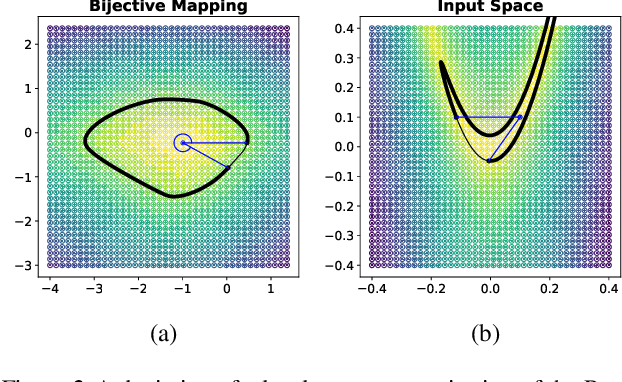
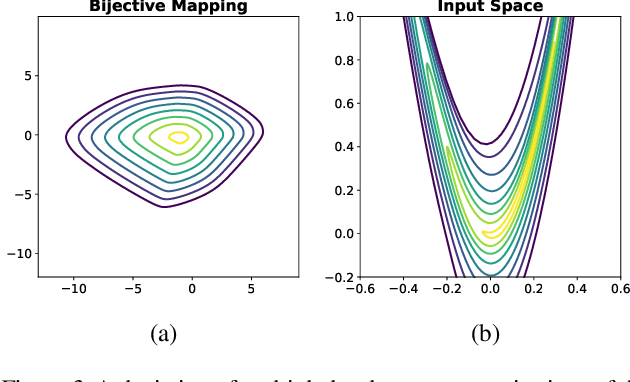
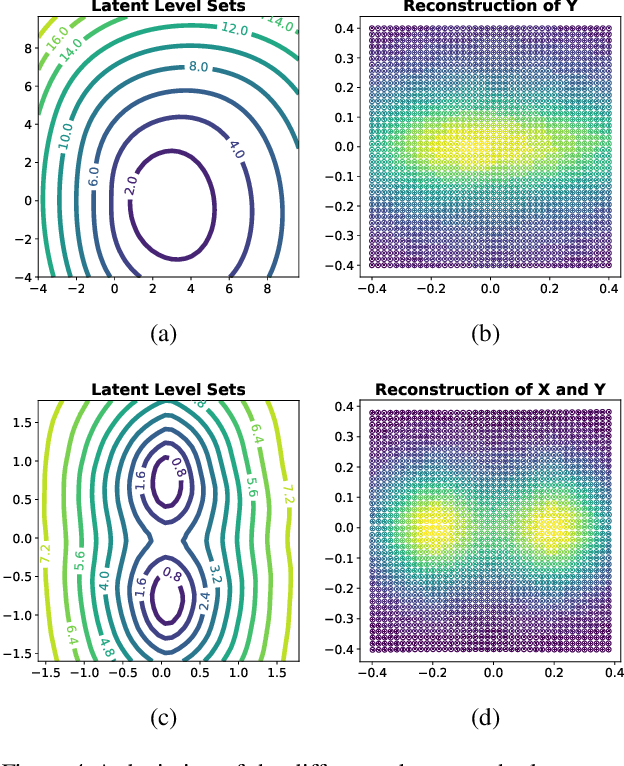
Considering smooth mappings from input vectors to continuous targets, our goal is to characterise subspaces of the input domain, which are invariant under such mappings. Thus, we want to characterise manifolds implicitly defined by level sets. Specifically, this characterisation should be of a global parametric form, which is especially useful for different informed data exploration tasks, such as building grid-based approximations, sampling points along the level curves, or finding trajectories on the manifold. However, global parameterisations can only exist if the level sets are connected. For this purpose, we introduce a novel and flexible class of neural networks that generalise input-convex networks. These networks represent functions that are guaranteed to have connected level sets forming smooth manifolds on the input space. We further show that global parameterisations of these level sets can be always found efficiently. Lastly, we demonstrate that our novel technique for characterising invariances is a powerful generative data exploration tool in real-world applications, such as computational chemistry.

Learning Conditional Invariance through Cycle Consistency

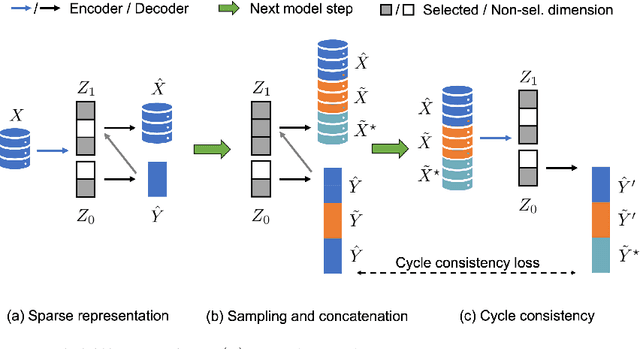
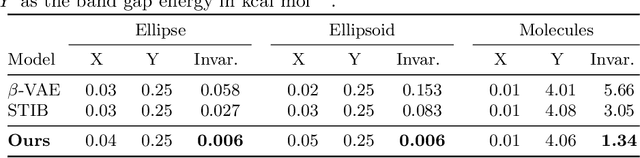
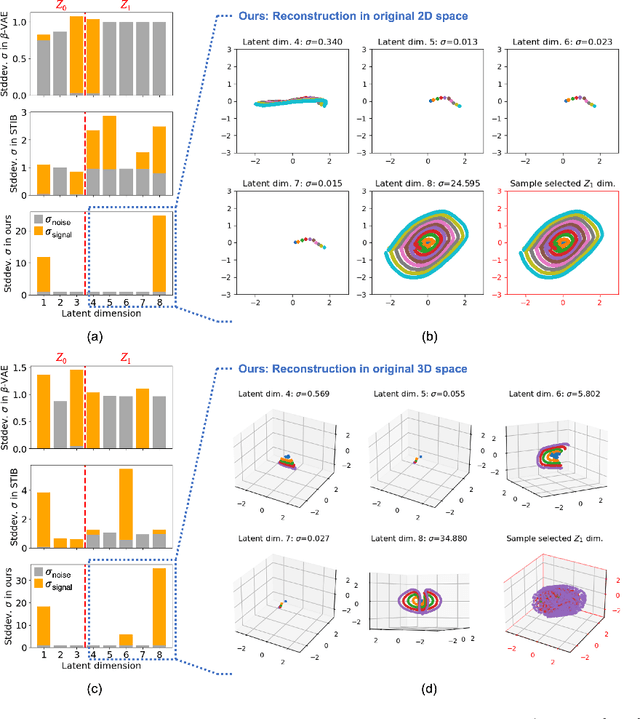
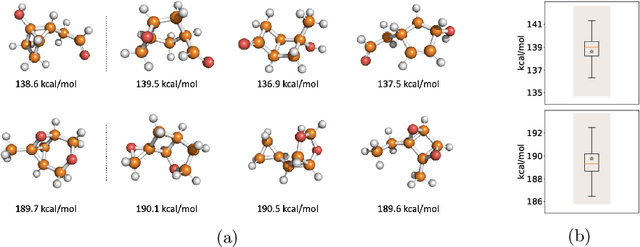
Identifying meaningful and independent factors of variation in a dataset is a challenging learning task frequently addressed by means of deep latent variable models. This task can be viewed as learning symmetry transformations preserving the value of a chosen property along latent dimensions. However, existing approaches exhibit severe drawbacks in enforcing the invariance property in the latent space. We address these shortcomings with a novel approach to cycle consistency. Our method involves two separate latent subspaces for the target property and the remaining input information, respectively. In order to enforce invariance as well as sparsity in the latent space, we incorporate semantic knowledge by using cycle consistency constraints relying on property side information. The proposed method is based on the deep information bottleneck and, in contrast to other approaches, allows using continuous target properties and provides inherent model selection capabilities. We demonstrate on synthetic and molecular data that our approach identifies more meaningful factors which lead to sparser and more interpretable models with improved invariance properties.

On the Empirical Neural Tangent Kernel of Standard Finite-Width Convolutional Neural Network Architectures

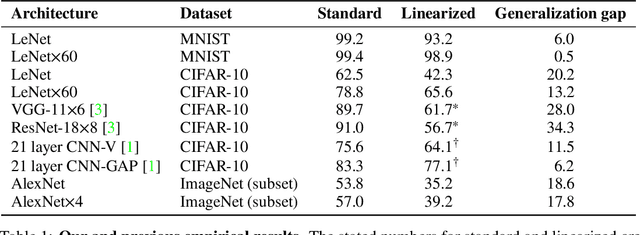
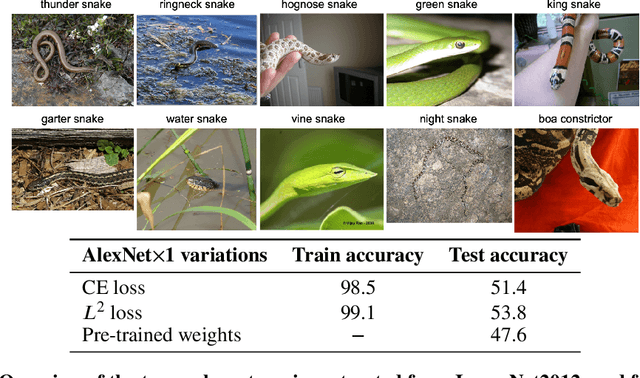
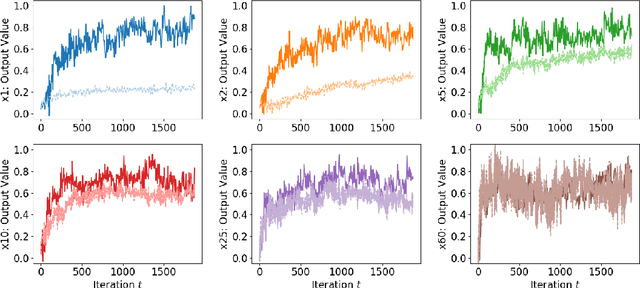
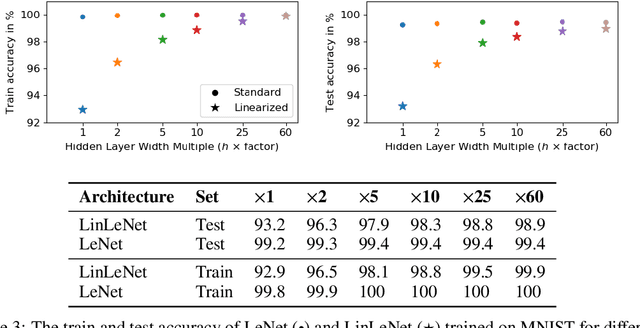
The Neural Tangent Kernel (NTK) is an important milestone in the ongoing effort to build a theory for deep learning. Its prediction that sufficiently wide neural networks behave as kernel methods, or equivalently as random feature models, has been confirmed empirically for certain wide architectures. It remains an open question how well NTK theory models standard neural network architectures of widths common in practice, trained on complex datasets such as ImageNet. We study this question empirically for two well-known convolutional neural network architectures, namely AlexNet and LeNet, and find that their behavior deviates significantly from their finite-width NTK counterparts. For wider versions of these networks, where the number of channels and widths of fully-connected layers are increased, the deviation decreases.

Learning Extremal Representations with Deep Archetypal Analysis

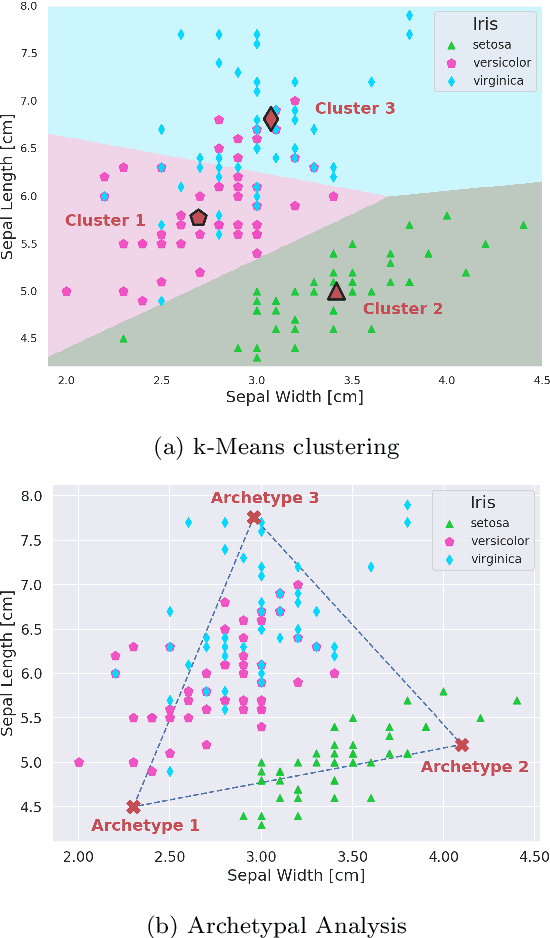
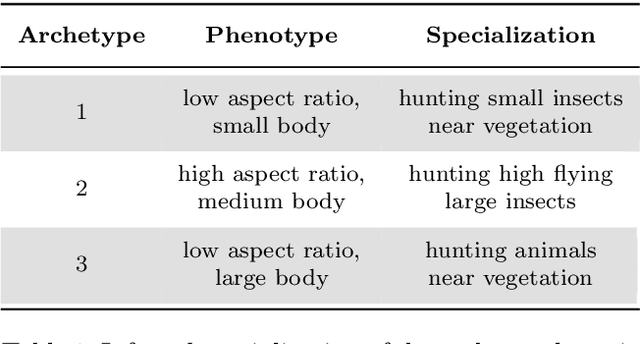
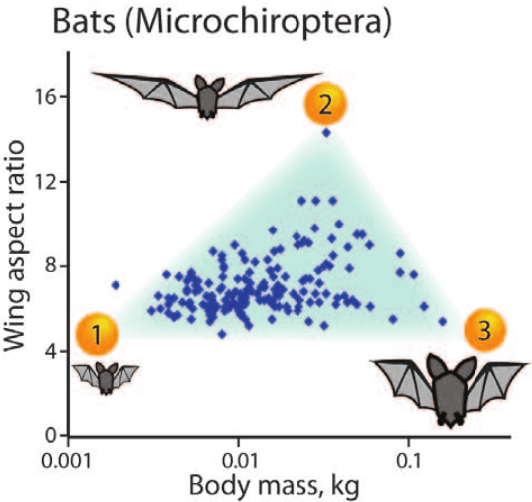
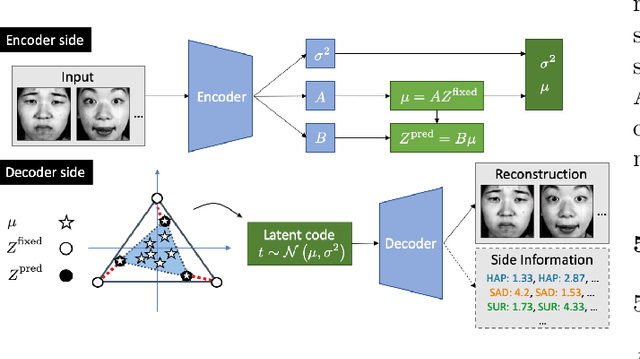
Archetypes are typical population representatives in an extremal sense, where typicality is understood as the most extreme manifestation of a trait or feature. In linear feature space, archetypes approximate the data convex hull allowing all data points to be expressed as convex mixtures of archetypes. However, it might not always be possible to identify meaningful archetypes in a given feature space. Learning an appropriate feature space and identifying suitable archetypes simultaneously addresses this problem. This paper introduces a generative formulation of the linear archetype model, parameterized by neural networks. By introducing the distance-dependent archetype loss, the linear archetype model can be integrated into the latent space of a variational autoencoder, and an optimal representation with respect to the unknown archetypes can be learned end-to-end. The reformulation of linear Archetypal Analysis as deep variational information bottleneck, allows the incorporation of arbitrarily complex side information during training. Furthermore, an alternative prior, based on a modified Dirichlet distribution, is proposed. The real-world applicability of the proposed method is demonstrated by exploring archetypes of female facial expressions while using multi-rater based emotion scores of these expressions as side information. A second application illustrates the exploration of the chemical space of small organic molecules. In this experiment, it is demonstrated that exchanging the side information but keeping the same set of molecules, e. g. using as side information the heat capacity of each molecule instead of the band gap energy, will result in the identification of different archetypes. As an application, these learned representations of chemical space might reveal distinct starting points for de novo molecular design.

Deep Archetypal Analysis

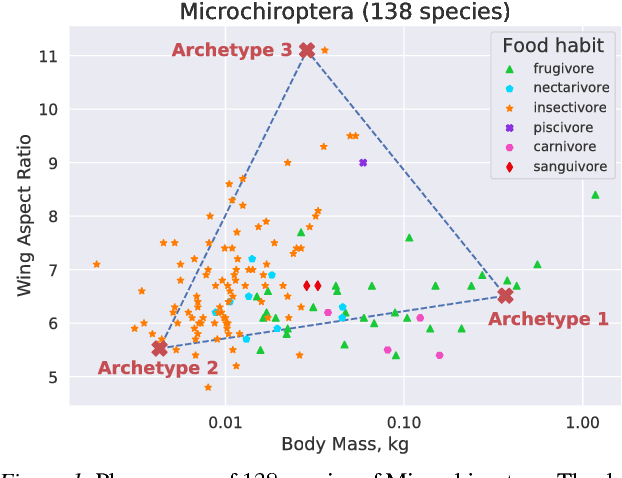
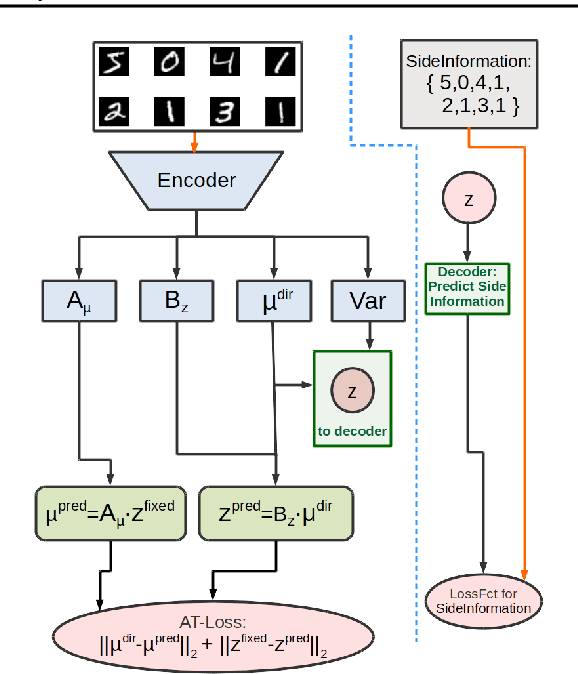
"Deep Archetypal Analysis" generates latent representations of high-dimensional datasets in terms of fractions of intuitively understandable basic entities called archetypes. The proposed method is an extension of linear "Archetypal Analysis" (AA), an unsupervised method to represent multivariate data points as sparse convex combinations of extremal elements of the dataset. Unlike the original formulation of AA, "Deep AA" can also handle side information and provides the ability for data-driven representation learning which reduces the dependence on expert knowledge. Our method is motivated by studies of evolutionary trade-offs in biology where archetypes are species highly adapted to a single task. Along these lines, we demonstrate that "Deep AA" also lends itself to the supervised exploration of chemical space, marking a distinct starting point for de novo molecular design. In the unsupervised setting we show how "Deep AA" is used on CelebA to identify archetypal faces. These can then be superimposed in order to generate new faces which inherit dominant traits of the archetypes they are based on.

Computational EEG in Personalized Medicine: A study in Parkinson's Disease

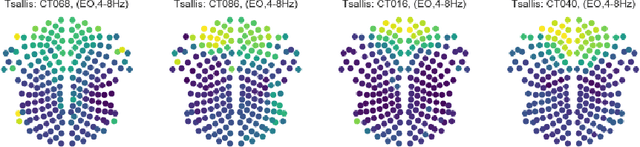
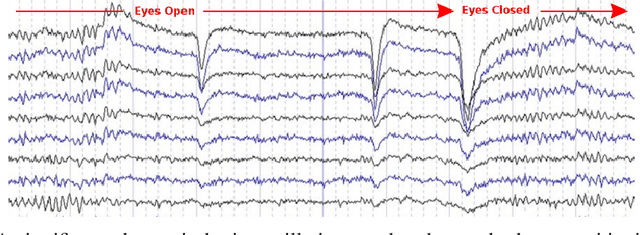
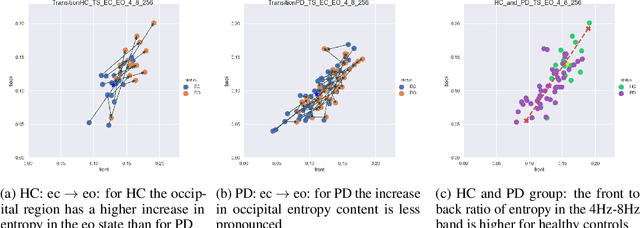
Recordings of electrical brain activity carry information about a person's cognitive health. For recording EEG signals, a very common setting is for a subject to be at rest with its eyes closed. Analysis of these recordings often involve a dimensionality reduction step in which electrodes are grouped into 10 or more regions (depending on the number of electrodes available). Then an average over each group is taken which serves as a feature in subsequent evaluation. Currently, the most prominent features used in clinical practice are based on spectral power densities. In our work we consider a simplified grouping of electrodes into two regions only. In addition to spectral features we introduce a secondary, non-redundant view on brain activity through the lens of Tsallis Entropy $S_{q=2}$. We further take EEG measurements not only in an eyes closed (ec) but also in an eyes open (eo) state. For our cohort of healthy controls (HC) and individuals suffering from Parkinson's disease (PD), the question we are asking is the following: How well can one discriminate between HC and PD within this simplified, binary grouping? This question is motivated by the commercial availability of inexpensive and easy to use portable EEG devices. If enough information is retained in this binary grouping, then such simple devices could potentially be used as personal monitoring tools, as standard screening tools by general practitioners or as digital biomarkers for easy long term monitoring during neurological studies.