Learning Extremal Representations with Deep Archetypal Analysis

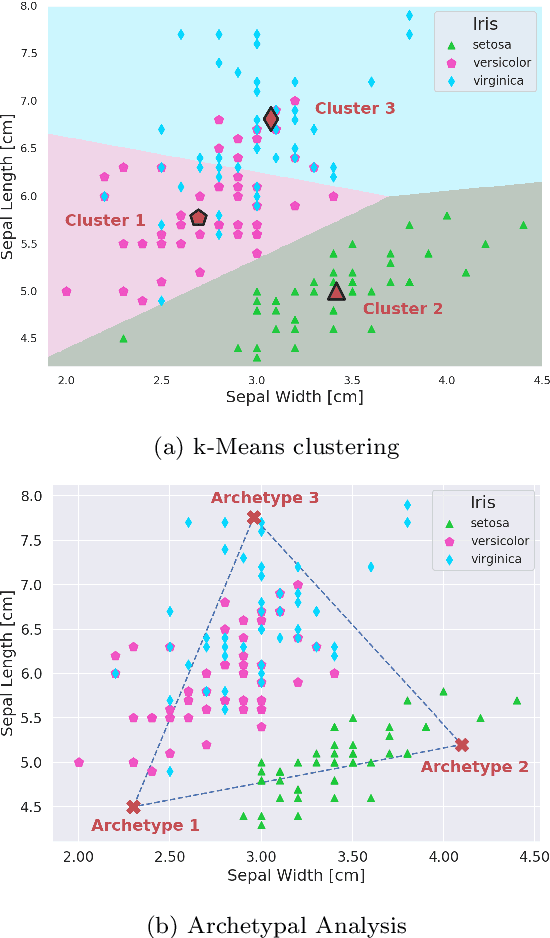
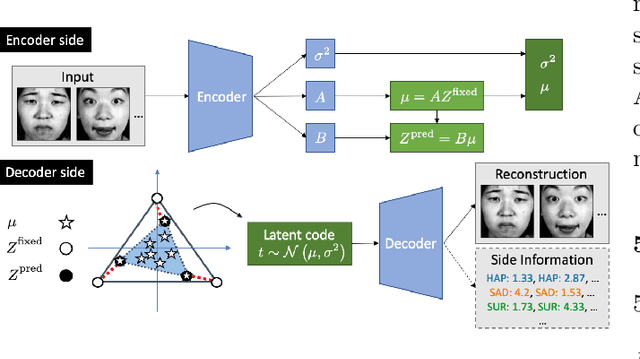
Archetypes are typical population representatives in an extremal sense, where typicality is understood as the most extreme manifestation of a trait or feature. In linear feature space, archetypes approximate the data convex hull allowing all data points to be expressed as convex mixtures of archetypes. However, it might not always be possible to identify meaningful archetypes in a given feature space. Learning an appropriate feature space and identifying suitable archetypes simultaneously addresses this problem. This paper introduces a generative formulation of the linear archetype model, parameterized by neural networks. By introducing the distance-dependent archetype loss, the linear archetype model can be integrated into the latent space of a variational autoencoder, and an optimal representation with respect to the unknown archetypes can be learned end-to-end. The reformulation of linear Archetypal Analysis as deep variational information bottleneck, allows the incorporation of arbitrarily complex side information during training. Furthermore, an alternative prior, based on a modified Dirichlet distribution, is proposed. The real-world applicability of the proposed method is demonstrated by exploring archetypes of female facial expressions while using multi-rater based emotion scores of these expressions as side information. A second application illustrates the exploration of the chemical space of small organic molecules. In this experiment, it is demonstrated that exchanging the side information but keeping the same set of molecules, e. g. using as side information the heat capacity of each molecule instead of the band gap energy, will result in the identification of different archetypes. As an application, these learned representations of chemical space might reveal distinct starting points for de novo molecular design.

Deep Archetypal Analysis

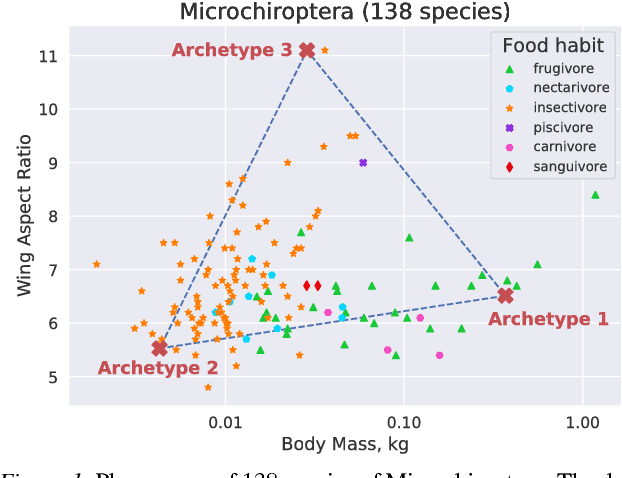
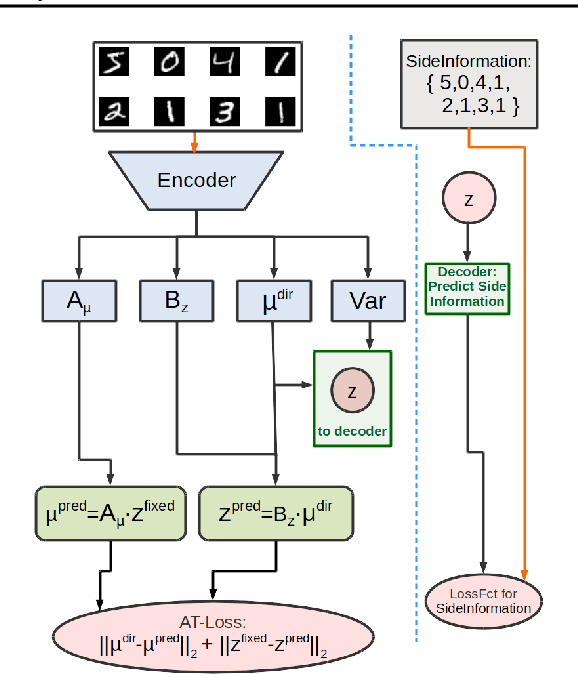
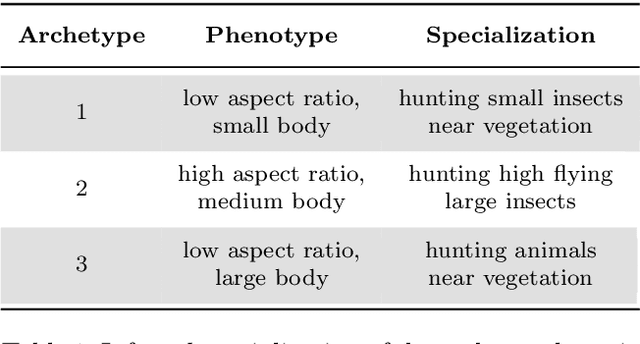
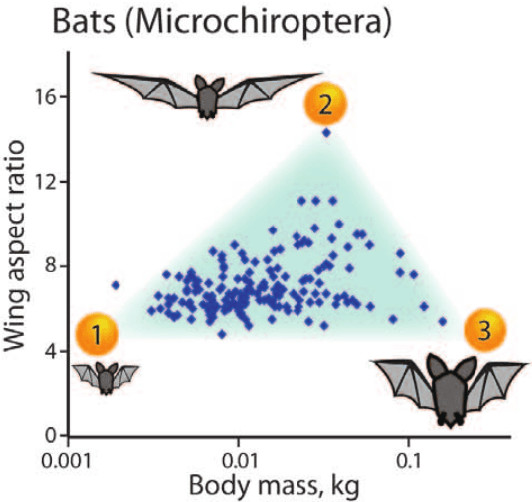
"Deep Archetypal Analysis" generates latent representations of high-dimensional datasets in terms of fractions of intuitively understandable basic entities called archetypes. The proposed method is an extension of linear "Archetypal Analysis" (AA), an unsupervised method to represent multivariate data points as sparse convex combinations of extremal elements of the dataset. Unlike the original formulation of AA, "Deep AA" can also handle side information and provides the ability for data-driven representation learning which reduces the dependence on expert knowledge. Our method is motivated by studies of evolutionary trade-offs in biology where archetypes are species highly adapted to a single task. Along these lines, we demonstrate that "Deep AA" also lends itself to the supervised exploration of chemical space, marking a distinct starting point for de novo molecular design. In the unsupervised setting we show how "Deep AA" is used on CelebA to identify archetypal faces. These can then be superimposed in order to generate new faces which inherit dominant traits of the archetypes they are based on.

Computational EEG in Personalized Medicine: A study in Parkinson's Disease

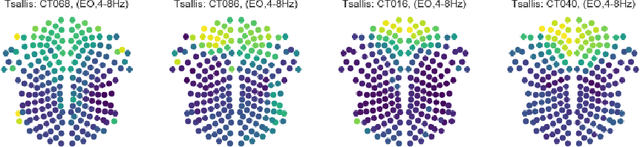
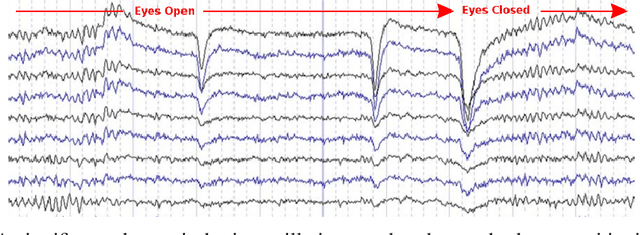
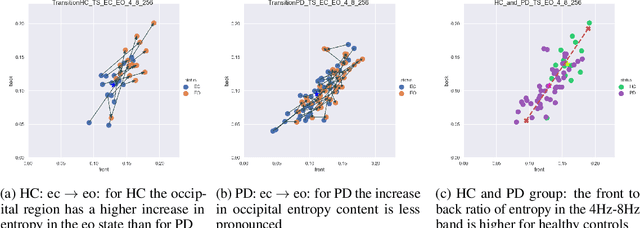
Recordings of electrical brain activity carry information about a person's cognitive health. For recording EEG signals, a very common setting is for a subject to be at rest with its eyes closed. Analysis of these recordings often involve a dimensionality reduction step in which electrodes are grouped into 10 or more regions (depending on the number of electrodes available). Then an average over each group is taken which serves as a feature in subsequent evaluation. Currently, the most prominent features used in clinical practice are based on spectral power densities. In our work we consider a simplified grouping of electrodes into two regions only. In addition to spectral features we introduce a secondary, non-redundant view on brain activity through the lens of Tsallis Entropy $S_{q=2}$. We further take EEG measurements not only in an eyes closed (ec) but also in an eyes open (eo) state. For our cohort of healthy controls (HC) and individuals suffering from Parkinson's disease (PD), the question we are asking is the following: How well can one discriminate between HC and PD within this simplified, binary grouping? This question is motivated by the commercial availability of inexpensive and easy to use portable EEG devices. If enough information is retained in this binary grouping, then such simple devices could potentially be used as personal monitoring tools, as standard screening tools by general practitioners or as digital biomarkers for easy long term monitoring during neurological studies.