Physics-Informed Boundary Integral Networks (PIBI-Nets): A Data-Driven Approach for Solving Partial Differential Equations

Partial differential equations (PDEs) can describe many relevant phenomena in dynamical systems. In real-world applications, we commonly need to combine formal PDE models with (potentially noisy) observations. This is especially relevant in settings where we lack information about boundary or initial conditions, or where we need to identify unknown model parameters. In recent years, Physics-informed neural networks (PINNs) have become a popular tool for problems of this kind. In high-dimensional settings, however, PINNs often suffer from computational problems because they usually require dense collocation points over the entire computational domain. To address this problem, we present Physics-Informed Boundary Integral Networks (PIBI-Nets) as a data-driven approach for solving PDEs in one dimension less than the original problem space. PIBI-Nets only need collocation points at the computational domain boundary, while still achieving highly accurate results, and in several practical settings, they clearly outperform PINNs. Exploiting elementary properties of fundamental solutions of linear differential operators, we present a principled and simple way to handle point sources in inverse problems. We demonstrate the excellent performance of PIBI-Nets for the Laplace and Poisson equations, both on artificial data sets and within a real-world application concerning the reconstruction of groundwater flows.

Truly Mesh-free Physics-Informed Neural Networks

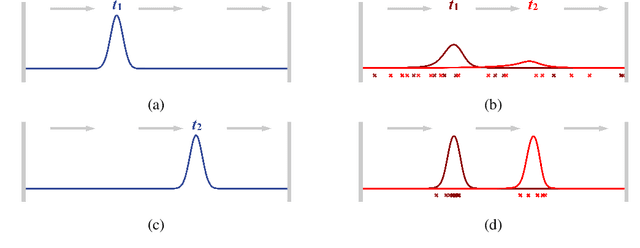
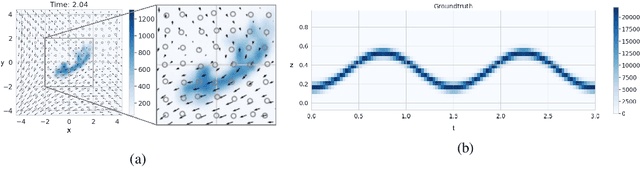
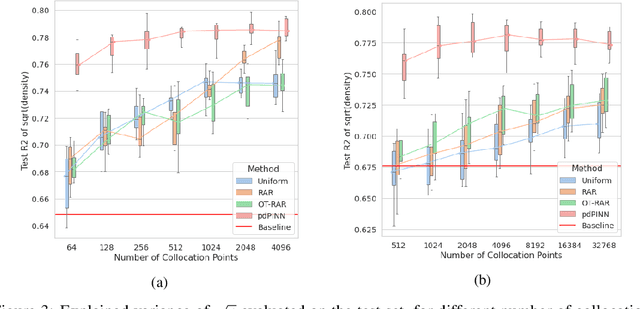
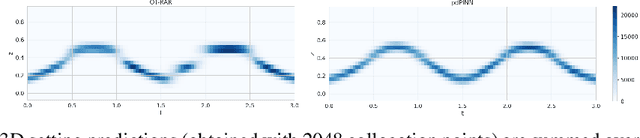
Physics-informed Neural Networks (PINNs) have recently emerged as a principled way to include prior physical knowledge in form of partial differential equations (PDEs) into neural networks. Although generally viewed as being mesh-free, current approaches still rely on collocation points obtained within a bounded region, even in settings with spatially sparse signals. Furthermore, if the boundaries are not known, the selection of such a region may be arbitrary, resulting in a large proportion of collocation points being selected in areas of low relevance. To resolve this, we present a mesh-free and adaptive approach termed particle-density PINN (pdPINN), which is inspired by the microscopic viewpoint of fluid dynamics. Instead of sampling from a bounded region, we propose to sample directly from the distribution over the (fluids) particle positions, eliminating the need to introduce boundaries while adaptively focusing on the most relevant regions. This is achieved by reformulating the modeled fluid density as an unnormalized probability distribution from which we sample with dynamic Monte Carlo methods. We further generalize pdPINNs to different settings that allow interpreting a positive scalar quantity as a particle density, such as the evolution of the temperature in the heat equation. The utility of our approach is demonstrated on experiments for modeling (non-steady) compressible fluids in up to three dimensions and a two-dimensional diffusion problem, illustrating the high flexibility and sample efficiency compared to existing refinement methods for PINNs.

Learning Invariances with Generalised Input-Convex Neural Networks

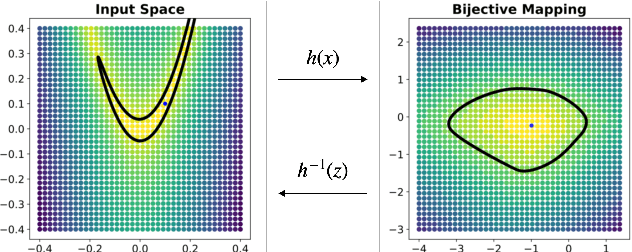
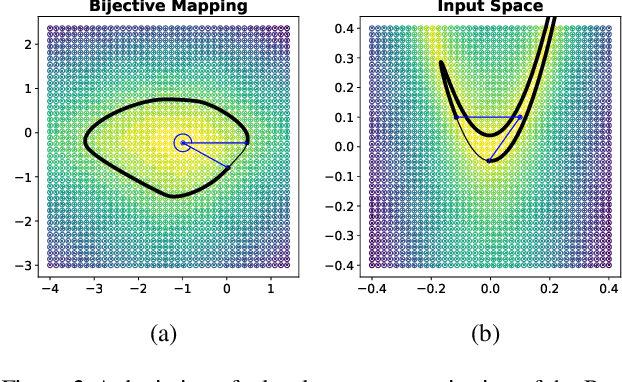
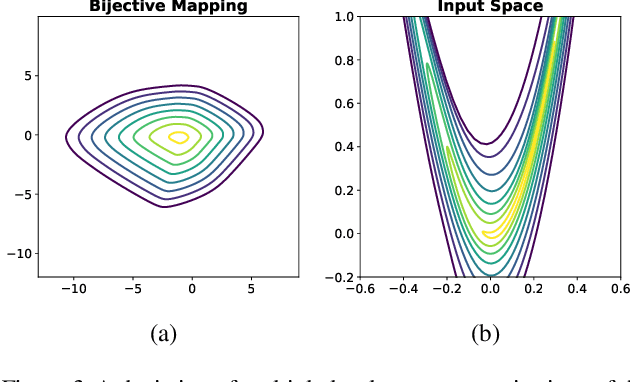
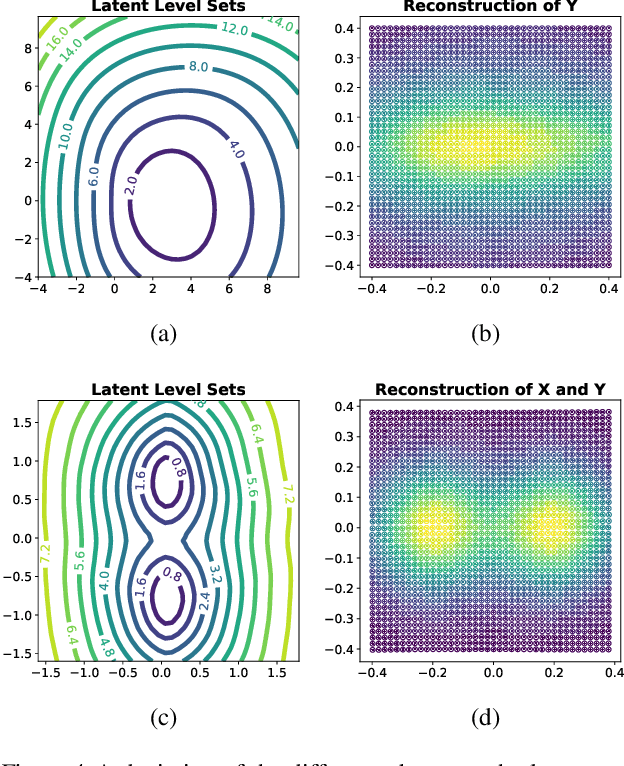
Considering smooth mappings from input vectors to continuous targets, our goal is to characterise subspaces of the input domain, which are invariant under such mappings. Thus, we want to characterise manifolds implicitly defined by level sets. Specifically, this characterisation should be of a global parametric form, which is especially useful for different informed data exploration tasks, such as building grid-based approximations, sampling points along the level curves, or finding trajectories on the manifold. However, global parameterisations can only exist if the level sets are connected. For this purpose, we introduce a novel and flexible class of neural networks that generalise input-convex networks. These networks represent functions that are guaranteed to have connected level sets forming smooth manifolds on the input space. We further show that global parameterisations of these level sets can be always found efficiently. Lastly, we demonstrate that our novel technique for characterising invariances is a powerful generative data exploration tool in real-world applications, such as computational chemistry.