Learning Invariances with Generalised Input-Convex Neural Networks

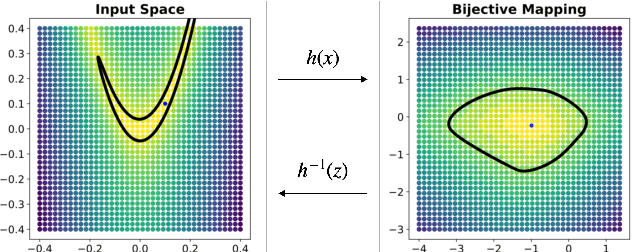
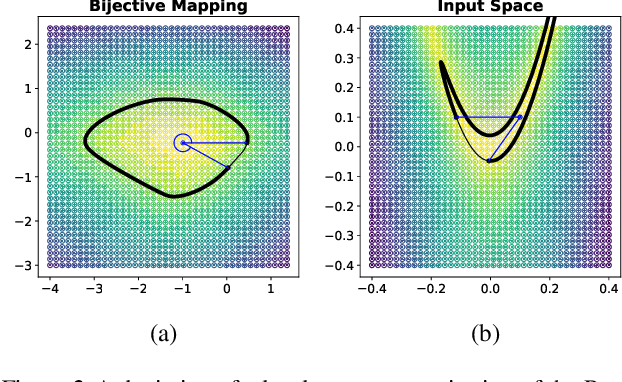
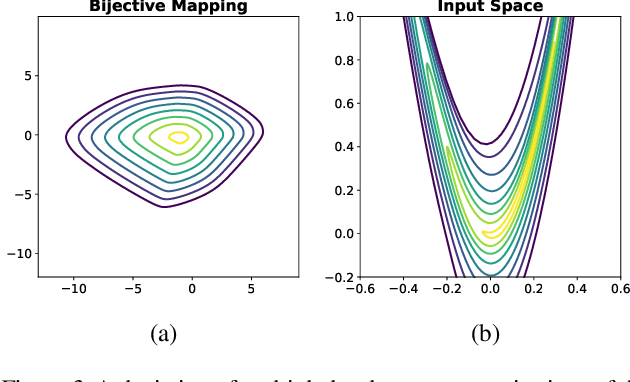
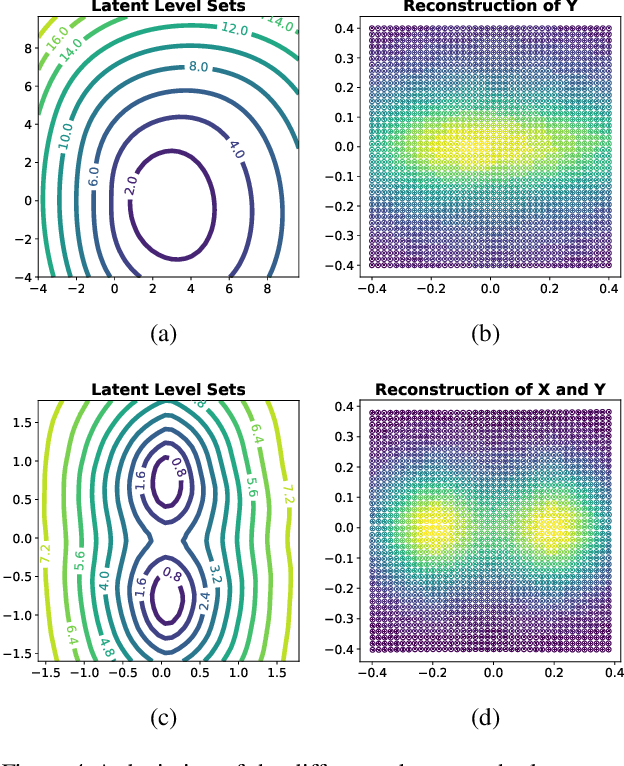
Considering smooth mappings from input vectors to continuous targets, our goal is to characterise subspaces of the input domain, which are invariant under such mappings. Thus, we want to characterise manifolds implicitly defined by level sets. Specifically, this characterisation should be of a global parametric form, which is especially useful for different informed data exploration tasks, such as building grid-based approximations, sampling points along the level curves, or finding trajectories on the manifold. However, global parameterisations can only exist if the level sets are connected. For this purpose, we introduce a novel and flexible class of neural networks that generalise input-convex networks. These networks represent functions that are guaranteed to have connected level sets forming smooth manifolds on the input space. We further show that global parameterisations of these level sets can be always found efficiently. Lastly, we demonstrate that our novel technique for characterising invariances is a powerful generative data exploration tool in real-world applications, such as computational chemistry.

Learning Conditional Invariance through Cycle Consistency

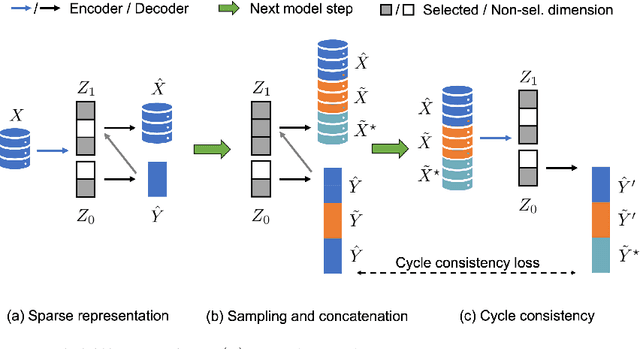
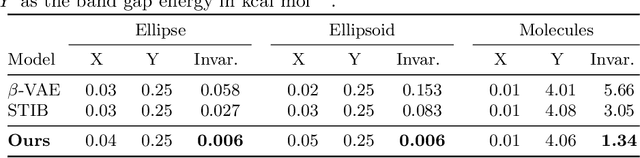
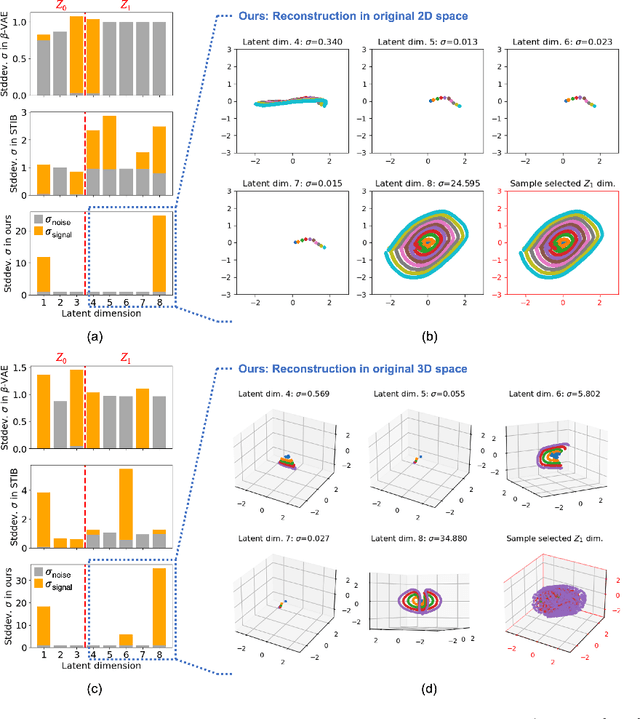
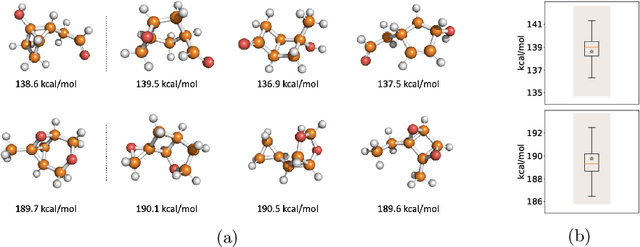
Identifying meaningful and independent factors of variation in a dataset is a challenging learning task frequently addressed by means of deep latent variable models. This task can be viewed as learning symmetry transformations preserving the value of a chosen property along latent dimensions. However, existing approaches exhibit severe drawbacks in enforcing the invariance property in the latent space. We address these shortcomings with a novel approach to cycle consistency. Our method involves two separate latent subspaces for the target property and the remaining input information, respectively. In order to enforce invariance as well as sparsity in the latent space, we incorporate semantic knowledge by using cycle consistency constraints relying on property side information. The proposed method is based on the deep information bottleneck and, in contrast to other approaches, allows using continuous target properties and provides inherent model selection capabilities. We demonstrate on synthetic and molecular data that our approach identifies more meaningful factors which lead to sparser and more interpretable models with improved invariance properties.

3DMolNet: A Generative Network for Molecular Structures

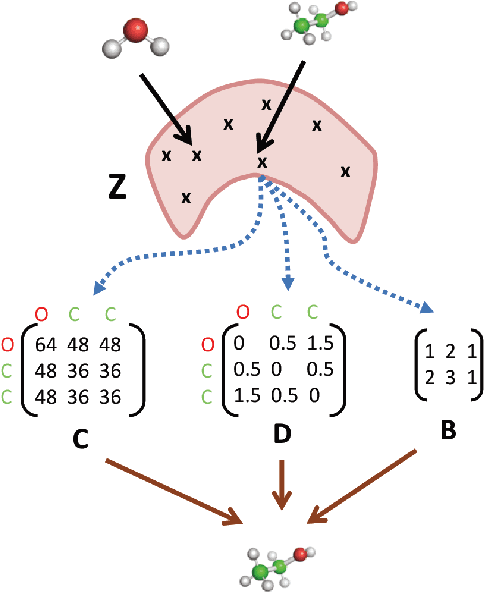
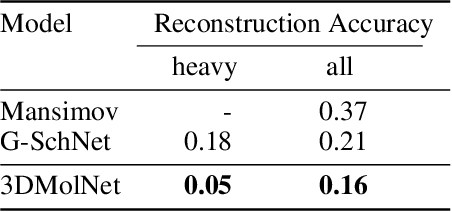
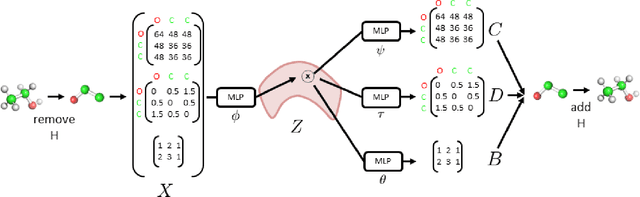
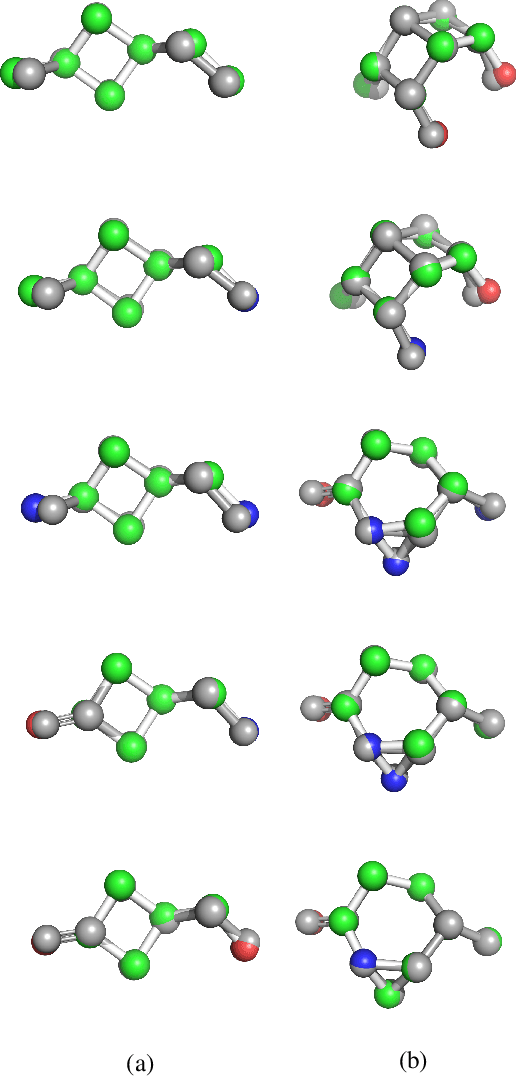
With the recent advances in machine learning for quantum chemistry, it is now possible to predict the chemical properties of compounds and to generate novel molecules. Existing generative models mostly use a string- or graph-based representation, but the precise three-dimensional coordinates of the atoms are usually not encoded. First attempts in this direction have been proposed, where autoregressive or GAN-based models generate atom coordinates. Those either lack a latent space in the autoregressive setting, such that a smooth exploration of the compound space is not possible, or cannot generalize to varying chemical compositions. We propose a new approach to efficiently generate molecular structures that are not restricted to a fixed size or composition. Our model is based on the variational autoencoder which learns a translation-, rotation-, and permutation-invariant low-dimensional representation of molecules. Our experiments yield a mean reconstruction error below 0.05 Angstrom, outperforming the current state-of-the-art methods by a factor of four, and which is even lower than the spatial quantization error of most chemical descriptors. The compositional and structural validity of newly generated molecules has been confirmed by quantum chemical methods in a set of experiments.