The future of cosmological likelihood-based inference: accelerated high-dimensional parameter estimation and model comparison

We advocate for a new paradigm of cosmological likelihood-based inference, leveraging recent developments in machine learning and its underlying technology, to accelerate Bayesian inference in high-dimensional settings. Specifically, we combine (i) emulation, where a machine learning model is trained to mimic cosmological observables, e.g. CosmoPower-JAX; (ii) differentiable and probabilistic programming, e.g. JAX and NumPyro, respectively; (iii) scalable Markov chain Monte Carlo (MCMC) sampling techniques that exploit gradients, e.g. Hamiltonian Monte Carlo; and (iv) decoupled and scalable Bayesian model selection techniques that compute the Bayesian evidence purely from posterior samples, e.g. the learned harmonic mean implemented in harmonic. This paradigm allows us to carry out a complete Bayesian analysis, including both parameter estimation and model selection, in a fraction of the time of traditional approaches. First, we demonstrate the application of this paradigm on a simulated cosmic shear analysis for a Stage IV survey in 37- and 39-dimensional parameter spaces, comparing $\Lambda$CDM and a dynamical dark energy model ($w_0w_a$CDM). We recover posterior contours and evidence estimates that are in excellent agreement with those computed by the traditional nested sampling approach while reducing the computational cost from 8 months on 48 CPU cores to 2 days on 12 GPUs. Second, we consider a joint analysis between three simulated next-generation surveys, each performing a 3x2pt analysis, resulting in 157- and 159-dimensional parameter spaces. Standard nested sampling techniques are simply not feasible in this high-dimensional setting, requiring a projected 12 years of compute time on 48 CPU cores; on the other hand, the proposed approach only requires 8 days of compute time on 24 GPUs. All packages used in our analyses are publicly available.

A representation learning approach to probe for dynamical dark energy in matter power spectra

We present DE-VAE, a variational autoencoder (VAE) architecture to search for a compressed representation of dynamical dark energy (DE) models in observational studies of the cosmic large-scale structure. DE-VAE is trained on matter power spectra boosts generated at wavenumbers $k\in(0.01-2.5) \ h/\rm{Mpc}$ and at four redshift values $z\in(0.1,0.48,0.78,1.5)$ for the most typical dynamical DE parametrization with two extra parameters describing an evolving DE equation of state. The boosts are compressed to a lower-dimensional representation, which is concatenated with standard cold dark matter (CDM) parameters and then mapped back to reconstructed boosts; both the compression and the reconstruction components are parametrized as neural networks. Remarkably, we find that a single latent parameter is sufficient to predict 95% (99%) of DE power spectra generated over a broad range of cosmological parameters within $1\sigma$ ($2\sigma$) of a Gaussian error which includes cosmic variance, shot noise and systematic effects for a Stage IV-like survey. This single parameter shows a high mutual information with the two DE parameters, and these three variables can be linked together with an explicit equation through symbolic regression. Considering a model with two latent variables only marginally improves the accuracy of the predictions, and adding a third latent variable has no significant impact on the model's performance. We discuss how the DE-VAE architecture can be extended from a proof of concept to a general framework to be employed in the search for a common lower-dimensional parametrization of a wide range of beyond-$\Lambda$CDM models and for different cosmological datasets. Such a framework could then both inform the development of cosmological surveys by targeting optimal probes, and provide theoretical insight into the common phenomenological aspects of beyond-$\Lambda$CDM models.

A robust estimator of mutual information for deep learning interpretability

We develop the use of mutual information (MI), a well-established metric in information theory, to interpret the inner workings of deep learning models. To accurately estimate MI from a finite number of samples, we present GMM-MI (pronounced $``$Jimmie$"$), an algorithm based on Gaussian mixture models that can be applied to both discrete and continuous settings. GMM-MI is computationally efficient, robust to the choice of hyperparameters and provides the uncertainty on the MI estimate due to the finite sample size. We extensively validate GMM-MI on toy data for which the ground truth MI is known, comparing its performance against established mutual information estimators. We then demonstrate the use of our MI estimator in the context of representation learning, working with synthetic data and physical datasets describing highly non-linear processes. We train deep learning models to encode high-dimensional data within a meaningful compressed (latent) representation, and use GMM-MI to quantify both the level of disentanglement between the latent variables, and their association with relevant physical quantities, thus unlocking the interpretability of the latent representation. We make GMM-MI publicly available.

Fast and realistic large-scale structure from machine-learning-augmented random field simulations

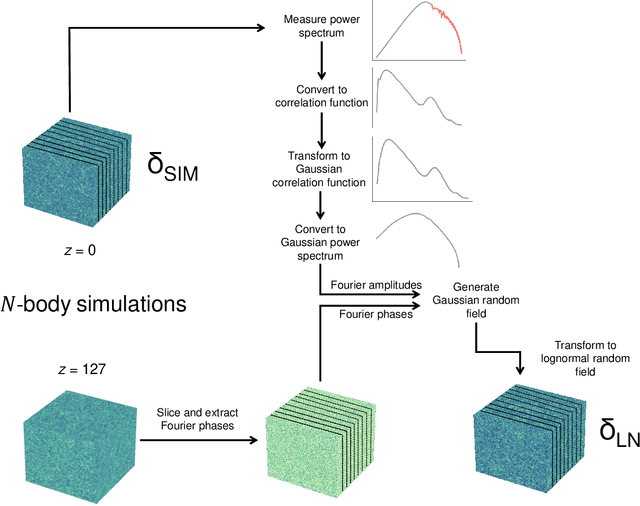
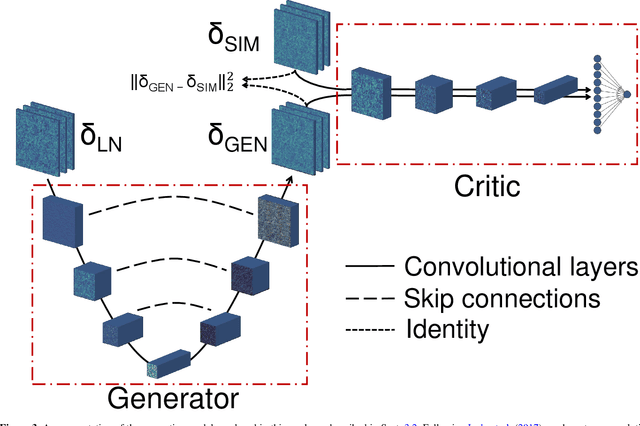
Producing thousands of simulations of the dark matter distribution in the Universe with increasing precision is a challenging but critical task to facilitate the exploitation of current and forthcoming cosmological surveys. Many inexpensive substitutes to full $N$-body simulations have been proposed, even though they often fail to reproduce the statistics of the smaller, non-linear scales. Among these alternatives, a common approximation is represented by the lognormal distribution, which comes with its own limitations as well, while being extremely fast to compute even for high-resolution density fields. In this work, we train a machine learning model to transform projected lognormal dark matter density fields to more realistic dark matter maps, as obtained from full $N$-body simulations. We detail the procedure that we follow to generate highly correlated pairs of lognormal and simulated maps, which we use as our training data, exploiting the information of the Fourier phases. We demonstrate the performance of our model comparing various statistical tests with different field resolutions, redshifts and cosmological parameters, proving its robustness and explaining its current limitations. The augmented lognormal random fields reproduce the power spectrum up to wavenumbers of $1 \ h \ \rm{Mpc}^{-1}$, the bispectrum and the peak counts within 10%, and always within the error bars, of the fiducial target simulations. Finally, we describe how we plan to integrate our proposed model with existing tools to yield more accurate spherical random fields for weak lensing analysis, going beyond the lognormal approximation.

Discovering the building blocks of dark matter halo density profiles with neural networks

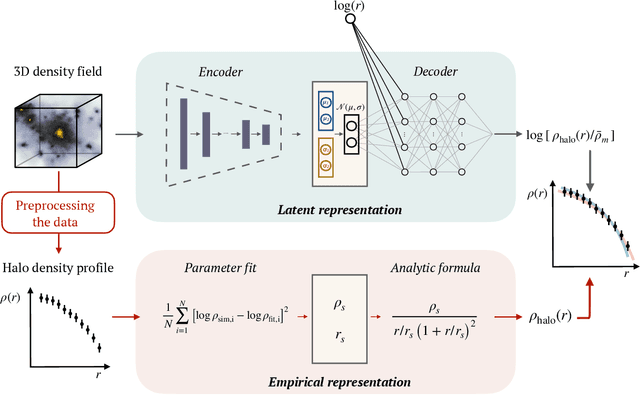
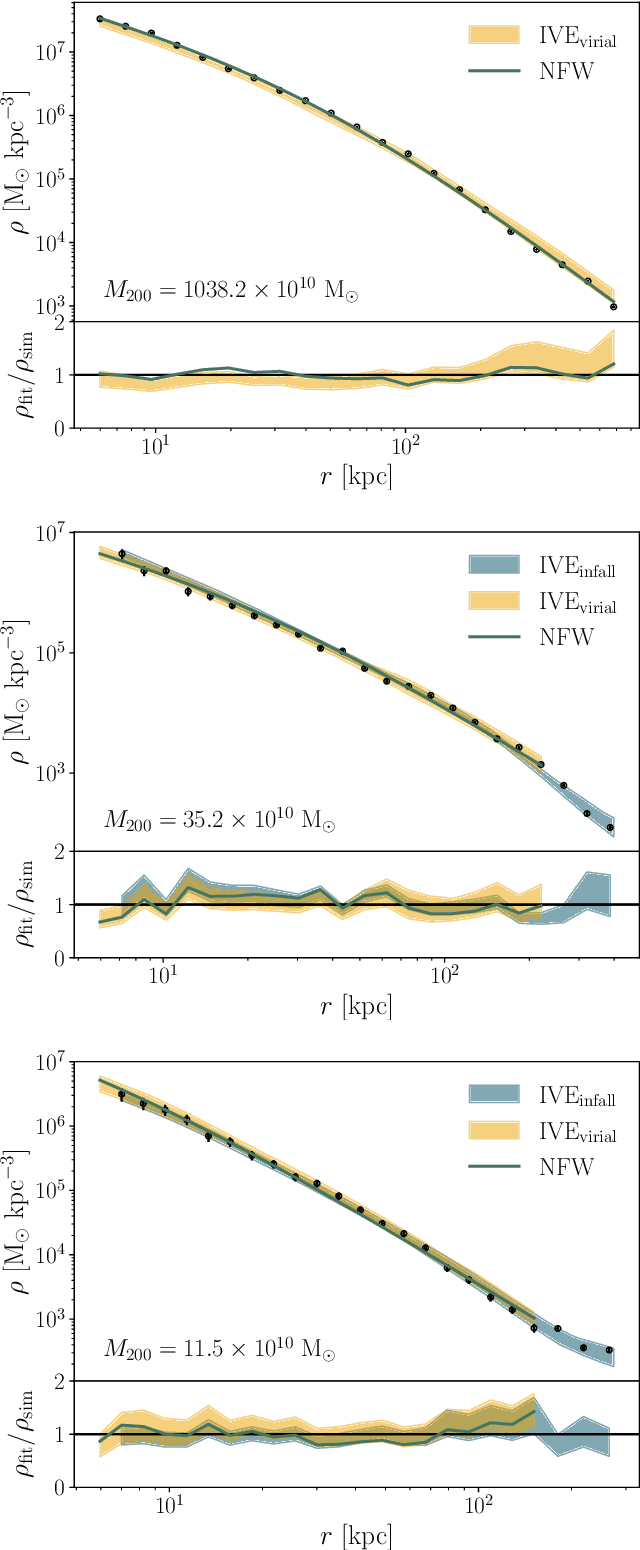
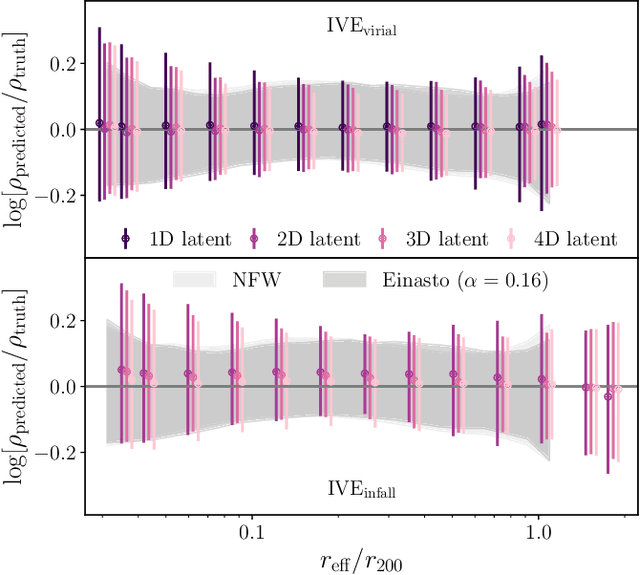
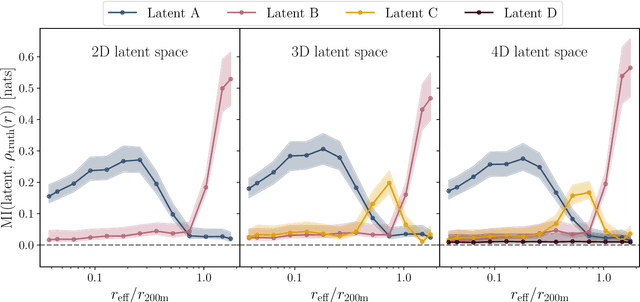
The density profiles of dark matter halos are typically modeled using empirical formulae fitted to the density profiles of relaxed halo populations. We present a neural network model that is trained to learn the mapping from the raw density field containing each halo to the dark matter density profile. We show that the model recovers the widely-used Navarro-Frenk-White (NFW) profile out to the virial radius, and can additionally describe the variability in the outer profile of the halos. The neural network architecture consists of a supervised encoder-decoder framework, which first compresses the density inputs into a low-dimensional latent representation, and then outputs $\rho(r)$ for any desired value of radius $r$. The latent representation contains all the information used by the model to predict the density profiles. This allows us to interpret the latent representation by quantifying the mutual information between the representation and the halos' ground-truth density profiles. A two-dimensional representation is sufficient to accurately model the density profiles up to the virial radius; however, a three-dimensional representation is required to describe the outer profiles beyond the virial radius. The additional dimension in the representation contains information about the infalling material in the outer profiles of dark matter halos, thus discovering the splashback boundary of halos without prior knowledge of the halos' dynamical history.

Towards fast machine-learning-assisted Bayesian posterior inference of realistic microseismic events

Bayesian inference applied to microseismic activity monitoring allows for principled estimation of the coordinates of microseismic events from recorded seismograms, and their associated uncertainties. However, forward modelling of these microseismic events, necessary to perform Bayesian source inversion, can be prohibitively expensive in terms of computational resources. A viable solution is to train a surrogate model based on machine learning techniques, to emulate the forward model and thus accelerate Bayesian inference. In this paper, we improve on previous work, which considered only sources with isotropic moment tensor. We train a machine learning algorithm on the power spectrum of the recorded pressure wave and show that the trained emulator allows for the complete and fast retrieval of the event coordinates for $\textit{any}$ source mechanism. Moreover, we show that our approach is computationally inexpensive, as it can be run in less than 1 hour on a commercial laptop, while yielding accurate results using less than $10^4$ training seismograms. We additionally demonstrate how the trained emulators can be used to identify the source mechanism through the estimation of the Bayesian evidence. This work lays the foundations for the efficient localisation and characterisation of any recorded seismogram, thus helping to quantify human impact on seismic activity and mitigate seismic hazard.

Learning to Noise: Application-Agnostic Data Sharing with Local Differential Privacy

In recent years, the collection and sharing of individuals' private data has become commonplace in many industries. Local differential privacy (LDP) is a rigorous approach which uses a randomized algorithm to preserve privacy even from the database administrator, unlike the more standard central differential privacy. For LDP, when applying noise directly to high-dimensional data, the level of noise required all but entirely destroys data utility. In this paper we introduce a novel, application-agnostic privatization mechanism that leverages representation learning to overcome the prohibitive noise requirements of direct methods, while maintaining the strict guarantees of LDP. We further demonstrate that this privatization mechanism can be used to train machine learning algorithms across a range of applications, including private data collection, private novel-class classification, and the augmentation of clean datasets with additional privatized features. We achieve significant gains in performance on downstream classification tasks relative to benchmarks that noise the data directly, which are state-of-the-art in the context of application-agnostic LDP mechanisms for high-dimensional data.