Fast and realistic large-scale structure from machine-learning-augmented random field simulations

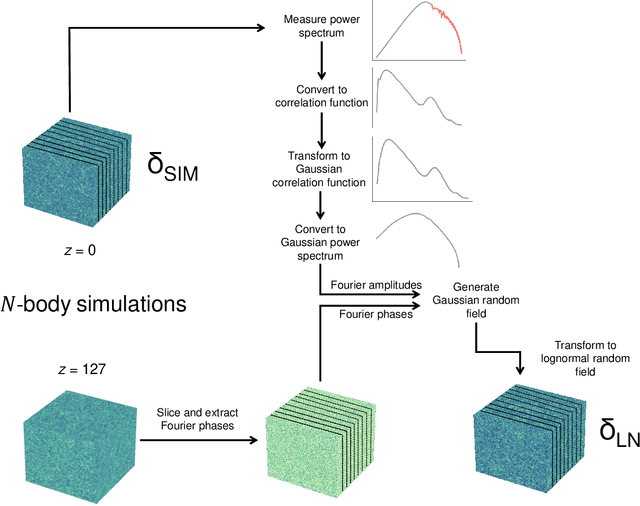
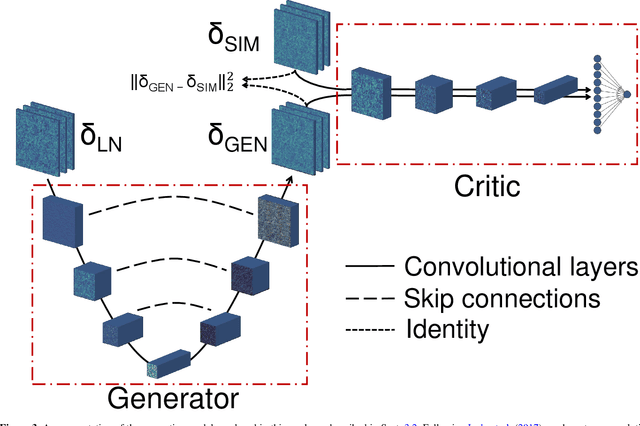
Producing thousands of simulations of the dark matter distribution in the Universe with increasing precision is a challenging but critical task to facilitate the exploitation of current and forthcoming cosmological surveys. Many inexpensive substitutes to full $N$-body simulations have been proposed, even though they often fail to reproduce the statistics of the smaller, non-linear scales. Among these alternatives, a common approximation is represented by the lognormal distribution, which comes with its own limitations as well, while being extremely fast to compute even for high-resolution density fields. In this work, we train a machine learning model to transform projected lognormal dark matter density fields to more realistic dark matter maps, as obtained from full $N$-body simulations. We detail the procedure that we follow to generate highly correlated pairs of lognormal and simulated maps, which we use as our training data, exploiting the information of the Fourier phases. We demonstrate the performance of our model comparing various statistical tests with different field resolutions, redshifts and cosmological parameters, proving its robustness and explaining its current limitations. The augmented lognormal random fields reproduce the power spectrum up to wavenumbers of $1 \ h \ \rm{Mpc}^{-1}$, the bispectrum and the peak counts within 10%, and always within the error bars, of the fiducial target simulations. Finally, we describe how we plan to integrate our proposed model with existing tools to yield more accurate spherical random fields for weak lensing analysis, going beyond the lognormal approximation.