Simulation-based inference with scattering representations: scattering is all you need

We demonstrate the first successful use of scattering representations without further compression for simulation-based inference (SBI) with images (i.e. field-level), illustrated with a cosmological case study. Scattering representations provide a highly effective representational space for subsequent learning tasks, although the higher dimensional compressed space introduces challenges. We overcome these through spatial averaging, coupled with more expressive density estimators. Compared to alternative methods, such an approach does not require additional simulations for either training or computing derivatives, is interpretable, and resilient to covariate shift. As expected, we show that a scattering only approach extracts more information than traditional second order summary statistics.

Fast and realistic large-scale structure from machine-learning-augmented random field simulations

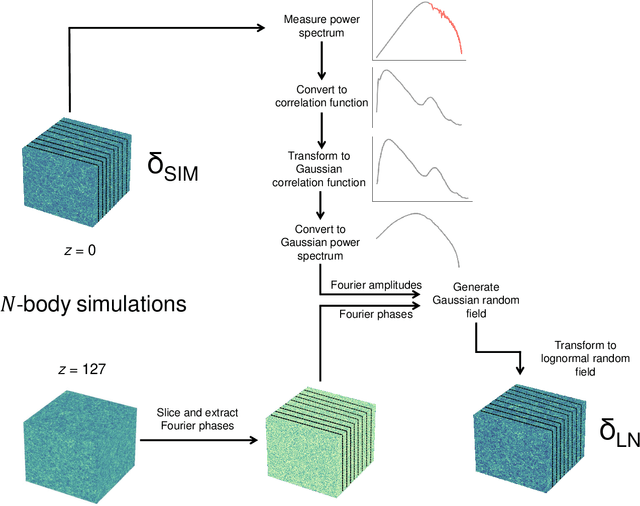
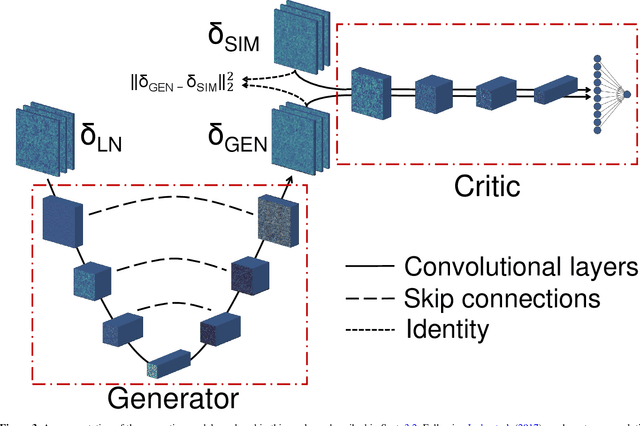
Producing thousands of simulations of the dark matter distribution in the Universe with increasing precision is a challenging but critical task to facilitate the exploitation of current and forthcoming cosmological surveys. Many inexpensive substitutes to full $N$-body simulations have been proposed, even though they often fail to reproduce the statistics of the smaller, non-linear scales. Among these alternatives, a common approximation is represented by the lognormal distribution, which comes with its own limitations as well, while being extremely fast to compute even for high-resolution density fields. In this work, we train a machine learning model to transform projected lognormal dark matter density fields to more realistic dark matter maps, as obtained from full $N$-body simulations. We detail the procedure that we follow to generate highly correlated pairs of lognormal and simulated maps, which we use as our training data, exploiting the information of the Fourier phases. We demonstrate the performance of our model comparing various statistical tests with different field resolutions, redshifts and cosmological parameters, proving its robustness and explaining its current limitations. The augmented lognormal random fields reproduce the power spectrum up to wavenumbers of $1 \ h \ \rm{Mpc}^{-1}$, the bispectrum and the peak counts within 10%, and always within the error bars, of the fiducial target simulations. Finally, we describe how we plan to integrate our proposed model with existing tools to yield more accurate spherical random fields for weak lensing analysis, going beyond the lognormal approximation.

Towards fast machine-learning-assisted Bayesian posterior inference of realistic microseismic events

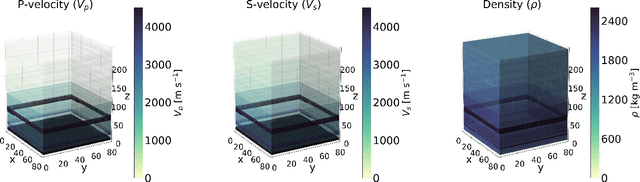
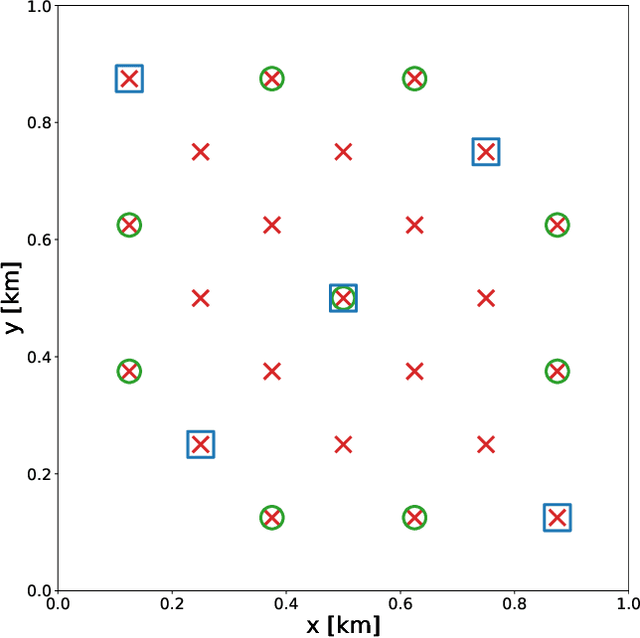
Bayesian inference applied to microseismic activity monitoring allows for principled estimation of the coordinates of microseismic events from recorded seismograms, and their associated uncertainties. However, forward modelling of these microseismic events, necessary to perform Bayesian source inversion, can be prohibitively expensive in terms of computational resources. A viable solution is to train a surrogate model based on machine learning techniques, to emulate the forward model and thus accelerate Bayesian inference. In this paper, we improve on previous work, which considered only sources with isotropic moment tensor. We train a machine learning algorithm on the power spectrum of the recorded pressure wave and show that the trained emulator allows for the complete and fast retrieval of the event coordinates for $\textit{any}$ source mechanism. Moreover, we show that our approach is computationally inexpensive, as it can be run in less than 1 hour on a commercial laptop, while yielding accurate results using less than $10^4$ training seismograms. We additionally demonstrate how the trained emulators can be used to identify the source mechanism through the estimation of the Bayesian evidence. This work lays the foundations for the efficient localisation and characterisation of any recorded seismogram, thus helping to quantify human impact on seismic activity and mitigate seismic hazard.