Towards fast machine-learning-assisted Bayesian posterior inference of realistic microseismic events

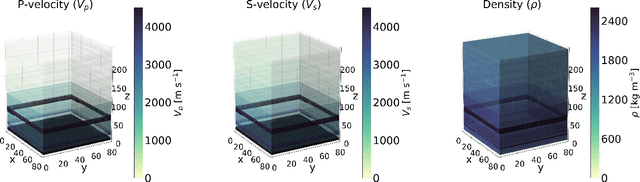
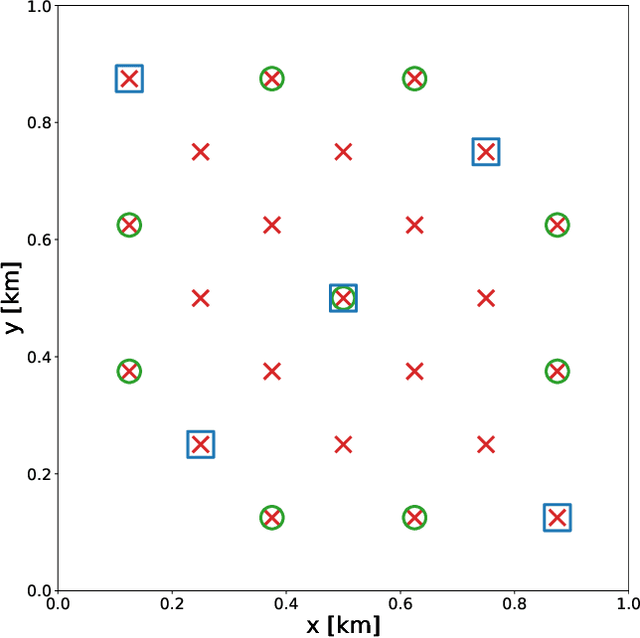
Bayesian inference applied to microseismic activity monitoring allows for principled estimation of the coordinates of microseismic events from recorded seismograms, and their associated uncertainties. However, forward modelling of these microseismic events, necessary to perform Bayesian source inversion, can be prohibitively expensive in terms of computational resources. A viable solution is to train a surrogate model based on machine learning techniques, to emulate the forward model and thus accelerate Bayesian inference. In this paper, we improve on previous work, which considered only sources with isotropic moment tensor. We train a machine learning algorithm on the power spectrum of the recorded pressure wave and show that the trained emulator allows for the complete and fast retrieval of the event coordinates for $\textit{any}$ source mechanism. Moreover, we show that our approach is computationally inexpensive, as it can be run in less than 1 hour on a commercial laptop, while yielding accurate results using less than $10^4$ training seismograms. We additionally demonstrate how the trained emulators can be used to identify the source mechanism through the estimation of the Bayesian evidence. This work lays the foundations for the efficient localisation and characterisation of any recorded seismogram, thus helping to quantify human impact on seismic activity and mitigate seismic hazard.

SKYNET: an efficient and robust neural network training tool for machine learning in astronomy

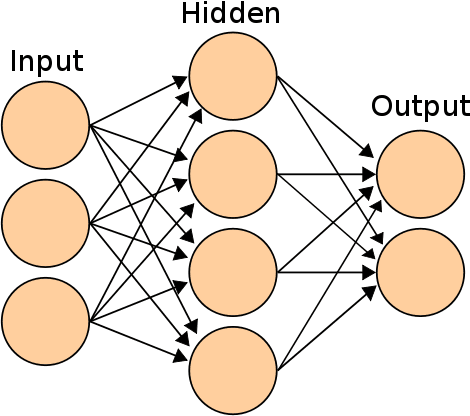
We present the first public release of our generic neural network training algorithm, called SkyNet. This efficient and robust machine learning tool is able to train large and deep feed-forward neural networks, including autoencoders, for use in a wide range of supervised and unsupervised learning applications, such as regression, classification, density estimation, clustering and dimensionality reduction. SkyNet uses a `pre-training' method to obtain a set of network parameters that has empirically been shown to be close to a good solution, followed by further optimisation using a regularised variant of Newton's method, where the level of regularisation is determined and adjusted automatically; the latter uses second-order derivative information to improve convergence, but without the need to evaluate or store the full Hessian matrix, by using a fast approximate method to calculate Hessian-vector products. This combination of methods allows for the training of complicated networks that are difficult to optimise using standard backpropagation techniques. SkyNet employs convergence criteria that naturally prevent overfitting, and also includes a fast algorithm for estimating the accuracy of network outputs. The utility and flexibility of SkyNet are demonstrated by application to a number of toy problems, and to astronomical problems focusing on the recovery of structure from blurred and noisy images, the identification of gamma-ray bursters, and the compression and denoising of galaxy images. The SkyNet software, which is implemented in standard ANSI C and fully parallelised using MPI, is available at http://www.mrao.cam.ac.uk/software/skynet/.

BAMBI: blind accelerated multimodal Bayesian inference

In this paper we present an algorithm for rapid Bayesian analysis that combines the benefits of nested sampling and artificial neural networks. The blind accelerated multimodal Bayesian inference (BAMBI) algorithm implements the MultiNest package for nested sampling as well as the training of an artificial neural network (NN) to learn the likelihood function. In the case of computationally expensive likelihoods, this allows the substitution of a much more rapid approximation in order to increase significantly the speed of the analysis. We begin by demonstrating, with a few toy examples, the ability of a NN to learn complicated likelihood surfaces. BAMBI's ability to decrease running time for Bayesian inference is then demonstrated in the context of estimating cosmological parameters from Wilkinson Microwave Anisotropy Probe and other observations. We show that valuable speed increases are achieved in addition to obtaining NNs trained on the likelihood functions for the different model and data combinations. These NNs can then be used for an even faster follow-up analysis using the same likelihood and different priors. This is a fully general algorithm that can be applied, without any pre-processing, to other problems with computationally expensive likelihood functions.