Bayesian automated posterior repartitioning for nested sampling

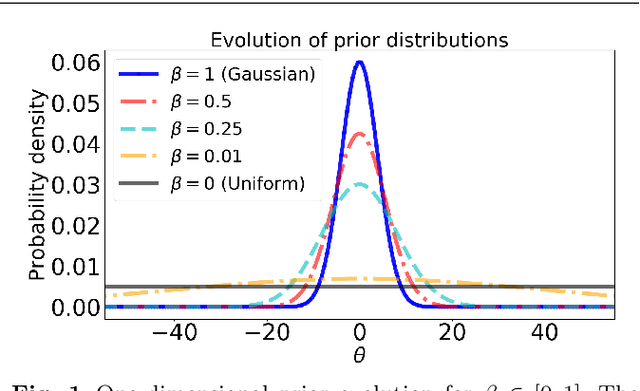
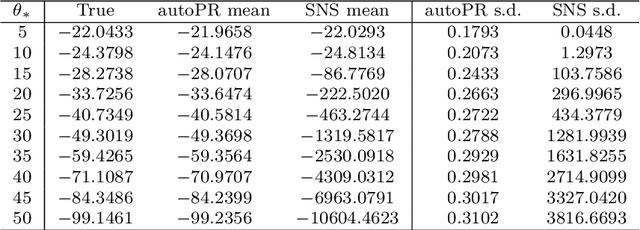
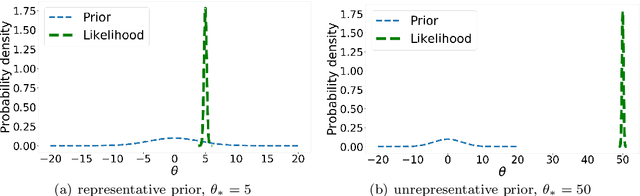
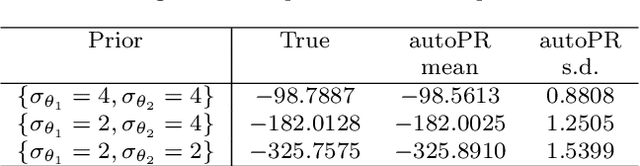
Priors in Bayesian analyses often encode informative domain knowledge that can be useful in making the inference process more efficient. Occasionally, however, priors may be unrepresentative of the parameter values for a given dataset, which can result in inefficient parameter space exploration, or even incorrect inferences, particularly for nested sampling (NS) algorithms. Simply broadening the prior in such cases may be inappropriate or impossible in some applications. Hence a previous solution of this problem, known as posterior repartitioning (PR), redefines the prior and likelihood while keeping their product fixed, so that the posterior inferences and evidence estimates remain unchanged, but the efficiency of the NS process is significantly increased. In its most practical form, PR raises the prior to some power $\beta$, which is introduced as an auxiliary variable that must be determined on a case-by-case basis, usually by lowering $\beta$ from unity according to some pre-defined `annealing schedule' until the resulting inferences converge to a consistent solution. We present here an alternative Bayesian `automated PR' method, in which $\beta$ is instead treated as a hyperparameter that is inferred from the data alongside the original parameters of the problem, and then marginalised over to obtain the final inference. We show through numerical examples that this approach provides a robust and efficient `hands-off' solution to addressing the issue of unrepresentative priors in Bayesian inference using NS. Moreover, we show that for problems with representative priors the method has a negligible computational overhead relative to standard nesting sampling, which suggests that it should be used in as a matter of course in all NS analyses.

SKYNET: an efficient and robust neural network training tool for machine learning in astronomy

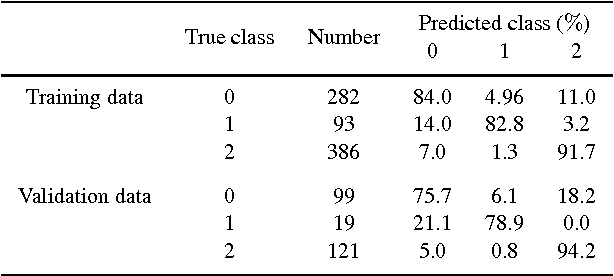
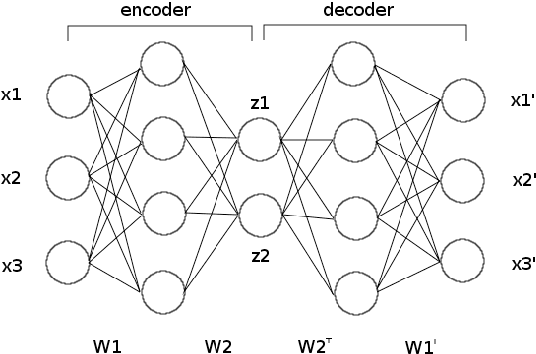
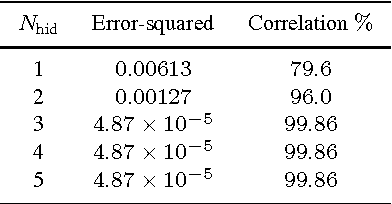
We present the first public release of our generic neural network training algorithm, called SkyNet. This efficient and robust machine learning tool is able to train large and deep feed-forward neural networks, including autoencoders, for use in a wide range of supervised and unsupervised learning applications, such as regression, classification, density estimation, clustering and dimensionality reduction. SkyNet uses a `pre-training' method to obtain a set of network parameters that has empirically been shown to be close to a good solution, followed by further optimisation using a regularised variant of Newton's method, where the level of regularisation is determined and adjusted automatically; the latter uses second-order derivative information to improve convergence, but without the need to evaluate or store the full Hessian matrix, by using a fast approximate method to calculate Hessian-vector products. This combination of methods allows for the training of complicated networks that are difficult to optimise using standard backpropagation techniques. SkyNet employs convergence criteria that naturally prevent overfitting, and also includes a fast algorithm for estimating the accuracy of network outputs. The utility and flexibility of SkyNet are demonstrated by application to a number of toy problems, and to astronomical problems focusing on the recovery of structure from blurred and noisy images, the identification of gamma-ray bursters, and the compression and denoising of galaxy images. The SkyNet software, which is implemented in standard ANSI C and fully parallelised using MPI, is available at http://www.mrao.cam.ac.uk/software/skynet/.

BAMBI: blind accelerated multimodal Bayesian inference

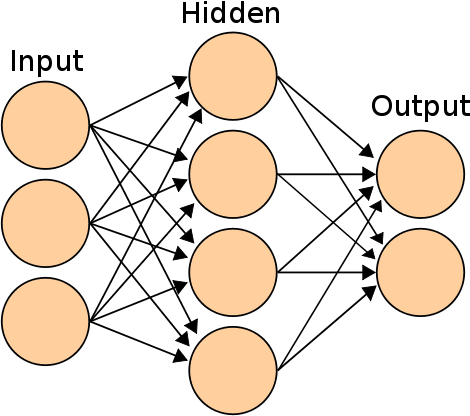
In this paper we present an algorithm for rapid Bayesian analysis that combines the benefits of nested sampling and artificial neural networks. The blind accelerated multimodal Bayesian inference (BAMBI) algorithm implements the MultiNest package for nested sampling as well as the training of an artificial neural network (NN) to learn the likelihood function. In the case of computationally expensive likelihoods, this allows the substitution of a much more rapid approximation in order to increase significantly the speed of the analysis. We begin by demonstrating, with a few toy examples, the ability of a NN to learn complicated likelihood surfaces. BAMBI's ability to decrease running time for Bayesian inference is then demonstrated in the context of estimating cosmological parameters from Wilkinson Microwave Anisotropy Probe and other observations. We show that valuable speed increases are achieved in addition to obtaining NNs trained on the likelihood functions for the different model and data combinations. These NNs can then be used for an even faster follow-up analysis using the same likelihood and different priors. This is a fully general algorithm that can be applied, without any pre-processing, to other problems with computationally expensive likelihood functions.