Kernel-, mean- and noise-marginalised Gaussian processes for exoplanet transits and $H_0$ inference

Using a fully Bayesian approach, Gaussian Process regression is extended to include marginalisation over the kernel choice and kernel hyperparameters. In addition, Bayesian model comparison via the evidence enables direct kernel comparison. The calculation of the joint posterior was implemented with a transdimensional sampler which simultaneously samples over the discrete kernel choice and their hyperparameters by embedding these in a higher-dimensional space, from which samples are taken using nested sampling. This method was explored on synthetic data from exoplanet transit light curve simulations. The true kernel was recovered in the low noise region while no kernel was preferred for larger noise. Furthermore, inference of the physical exoplanet hyperparameters was conducted. In the high noise region, either the bias in the posteriors was removed, the posteriors were broadened or the accuracy of the inference was increased. In addition, the uncertainty in mean function predictive distribution increased due to the uncertainty in the kernel choice. Subsequently, the method was extended to marginalisation over mean functions and noise models and applied to the inference of the present-day Hubble parameter, $H_0$, from real measurements of the Hubble parameter as a function of redshift, derived from the cosmologically model-independent cosmic chronometer and {\Lambda}CDM-dependent baryon acoustic oscillation observations. The inferred $H_0$ values from the cosmic chronometers, baryon acoustic oscillations and combined datasets are $H_0$ = 66$\pm$6 km/s/Mpc, $H_0$ = 67$\pm$10 km/s/Mpc and $H_0$ = 69$\pm$6 km/s/Mpc, respectively. The kernel posterior of the cosmic chronometers dataset prefers a non-stationary linear kernel. Finally, the datasets are shown to be not in tension with ln(R)=12.17$\pm$0.02.

Bayesian automated posterior repartitioning for nested sampling

Priors in Bayesian analyses often encode informative domain knowledge that can be useful in making the inference process more efficient. Occasionally, however, priors may be unrepresentative of the parameter values for a given dataset, which can result in inefficient parameter space exploration, or even incorrect inferences, particularly for nested sampling (NS) algorithms. Simply broadening the prior in such cases may be inappropriate or impossible in some applications. Hence a previous solution of this problem, known as posterior repartitioning (PR), redefines the prior and likelihood while keeping their product fixed, so that the posterior inferences and evidence estimates remain unchanged, but the efficiency of the NS process is significantly increased. In its most practical form, PR raises the prior to some power $\beta$, which is introduced as an auxiliary variable that must be determined on a case-by-case basis, usually by lowering $\beta$ from unity according to some pre-defined `annealing schedule' until the resulting inferences converge to a consistent solution. We present here an alternative Bayesian `automated PR' method, in which $\beta$ is instead treated as a hyperparameter that is inferred from the data alongside the original parameters of the problem, and then marginalised over to obtain the final inference. We show through numerical examples that this approach provides a robust and efficient `hands-off' solution to addressing the issue of unrepresentative priors in Bayesian inference using NS. Moreover, we show that for problems with representative priors the method has a negligible computational overhead relative to standard nesting sampling, which suggests that it should be used in as a matter of course in all NS analyses.

Bayesian sparse reconstruction: a brute-force approach to astronomical imaging and machine learning

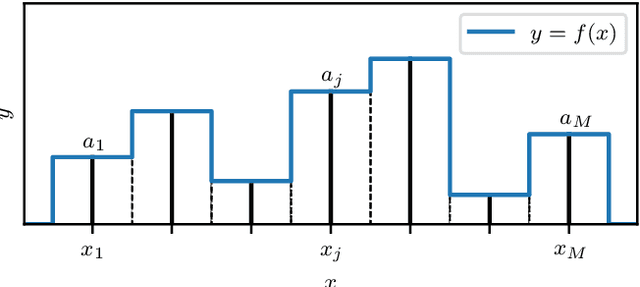
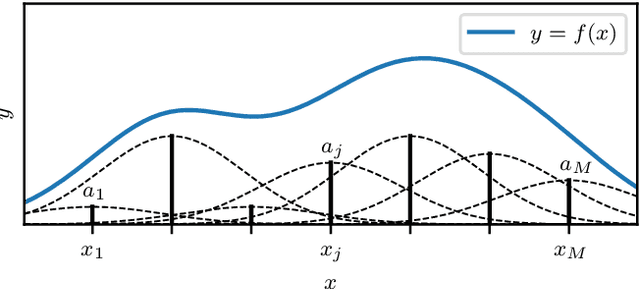
We present a principled Bayesian framework for signal reconstruction, in which the signal is modelled by basis functions whose number (and form, if required) is determined by the data themselves. This approach is based on a Bayesian interpretation of conventional sparse reconstruction and regularisation techniques, in which sparsity is imposed through priors via Bayesian model selection. We demonstrate our method for noisy 1- and 2-dimensional signals, including astronomical images. Furthermore, by using a product-space approach, the number and type of basis functions can be treated as integer parameters and their posterior distributions sampled directly. We show that order-of-magnitude increases in computational efficiency are possible from this technique compared to calculating the Bayesian evidences separately, and that further computational gains are possible using it in combination with dynamic nested sampling. Our approach can be readily applied to neural networks, where it allows the network architecture to be determined by the data in a principled Bayesian manner by treating the number of nodes and hidden layers as parameters.