GALILEO: A Generalized Low-Entropy Mixture Model

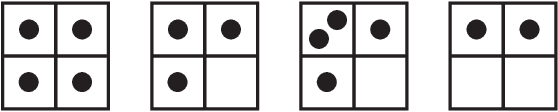
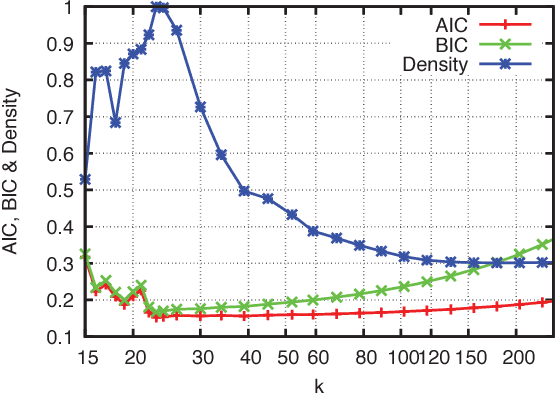
We present a new method of generating mixture models for data with categorical attributes. The keys to this approach are an entropy-based density metric in categorical space and annealing of high-entropy/low-density components from an initial state with many components. Pruning of low-density components using the entropy-based density allows GALILEO to consistently find high-quality clusters and the same optimal number of clusters. GALILEO has shown promising results on a range of test datasets commonly used for categorical clustering benchmarks. We demonstrate that the scaling of GALILEO is linear in the number of records in the dataset, making this method suitable for very large categorical datasets.

Bayesian Learning of Clique Tree Structure

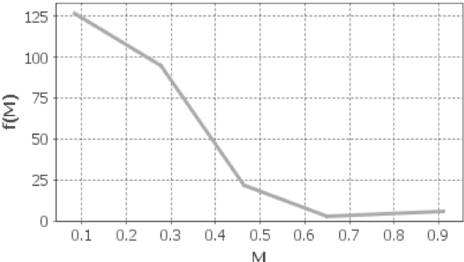
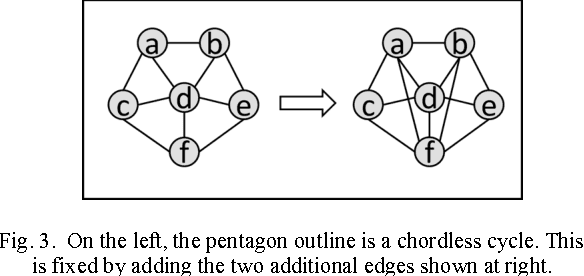
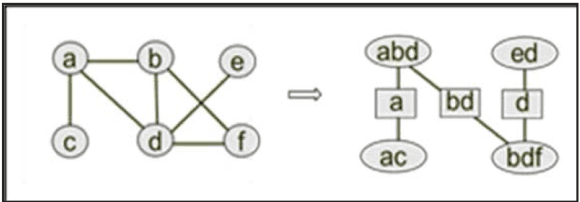
The problem of categorical data analysis in high dimensions is considered. A discussion of the fundamental difficulties of probability modeling is provided, and a solution to the derivation of high dimensional probability distributions based on Bayesian learning of clique tree decomposition is presented. The main contributions of this paper are an automated determination of the optimal clique tree structure for probability modeling, the resulting derived probability distribution, and a corresponding unified approach to clustering and anomaly detection based on the probability distribution.

SKYNET: an efficient and robust neural network training tool for machine learning in astronomy

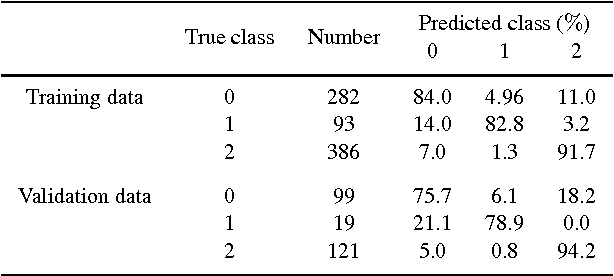
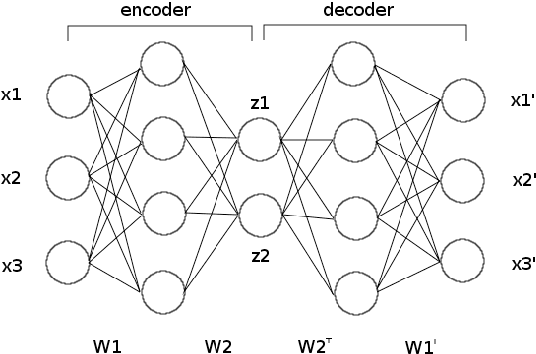
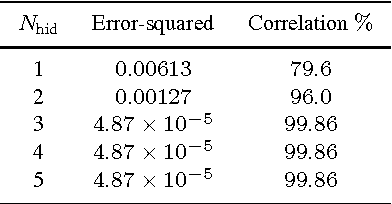
We present the first public release of our generic neural network training algorithm, called SkyNet. This efficient and robust machine learning tool is able to train large and deep feed-forward neural networks, including autoencoders, for use in a wide range of supervised and unsupervised learning applications, such as regression, classification, density estimation, clustering and dimensionality reduction. SkyNet uses a `pre-training' method to obtain a set of network parameters that has empirically been shown to be close to a good solution, followed by further optimisation using a regularised variant of Newton's method, where the level of regularisation is determined and adjusted automatically; the latter uses second-order derivative information to improve convergence, but without the need to evaluate or store the full Hessian matrix, by using a fast approximate method to calculate Hessian-vector products. This combination of methods allows for the training of complicated networks that are difficult to optimise using standard backpropagation techniques. SkyNet employs convergence criteria that naturally prevent overfitting, and also includes a fast algorithm for estimating the accuracy of network outputs. The utility and flexibility of SkyNet are demonstrated by application to a number of toy problems, and to astronomical problems focusing on the recovery of structure from blurred and noisy images, the identification of gamma-ray bursters, and the compression and denoising of galaxy images. The SkyNet software, which is implemented in standard ANSI C and fully parallelised using MPI, is available at http://www.mrao.cam.ac.uk/software/skynet/.

BAMBI: blind accelerated multimodal Bayesian inference

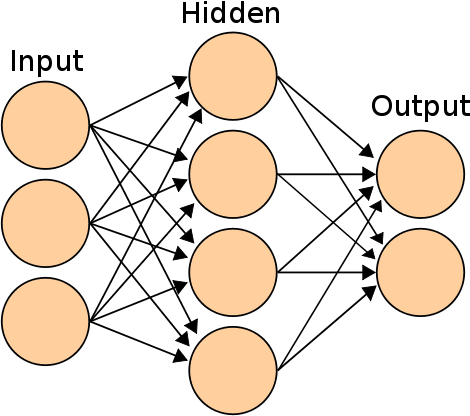
In this paper we present an algorithm for rapid Bayesian analysis that combines the benefits of nested sampling and artificial neural networks. The blind accelerated multimodal Bayesian inference (BAMBI) algorithm implements the MultiNest package for nested sampling as well as the training of an artificial neural network (NN) to learn the likelihood function. In the case of computationally expensive likelihoods, this allows the substitution of a much more rapid approximation in order to increase significantly the speed of the analysis. We begin by demonstrating, with a few toy examples, the ability of a NN to learn complicated likelihood surfaces. BAMBI's ability to decrease running time for Bayesian inference is then demonstrated in the context of estimating cosmological parameters from Wilkinson Microwave Anisotropy Probe and other observations. We show that valuable speed increases are achieved in addition to obtaining NNs trained on the likelihood functions for the different model and data combinations. These NNs can then be used for an even faster follow-up analysis using the same likelihood and different priors. This is a fully general algorithm that can be applied, without any pre-processing, to other problems with computationally expensive likelihood functions.