Cetin Savkli
Random Subspace Mixture Models for Interpretable Anomaly Detection
Aug 13, 2021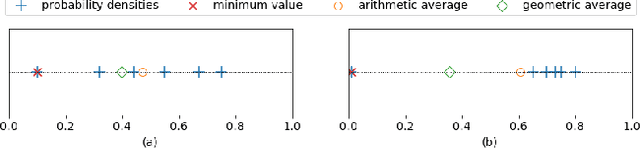
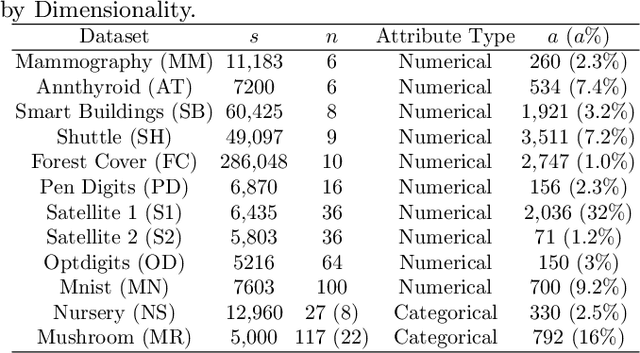
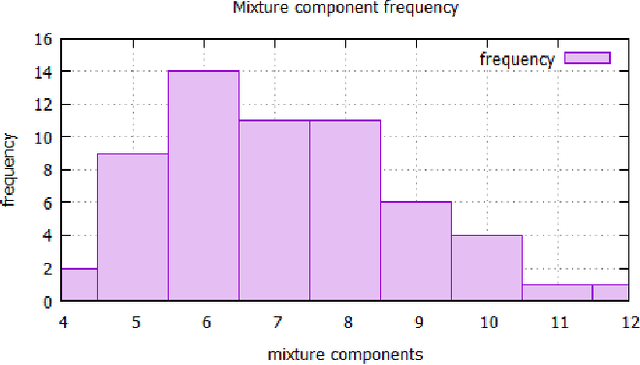
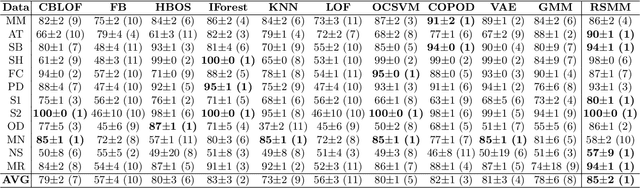
Abstract:We present a new subspace-based method to construct probabilistic models for high-dimensional data and highlight its use in anomaly detection. The approach is based on a statistical estimation of probability density using densities of random subspaces combined with geometric averaging. In selecting random subspaces, equal representation of each attribute is used to ensure correct statistical limits. Gaussian mixture models (GMMs) are used to create the probability densities for each subspace with techniques included to mitigate singularities allowing for the ability to handle both numerical and categorial attributes. The number of components for each GMM is determined automatically through Bayesian information criterion to prevent overfitting. The proposed algorithm attains competitive AUC scores compared with prominent algorithms against benchmark anomaly detection datasets with the added benefits of being simple, scalable, and interpretable.
* 10 pages
Novel Edge and Density Metrics for Link Cohesion
Mar 06, 2020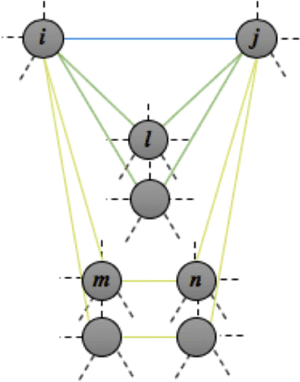
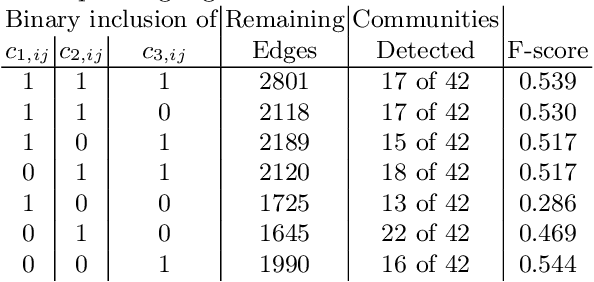
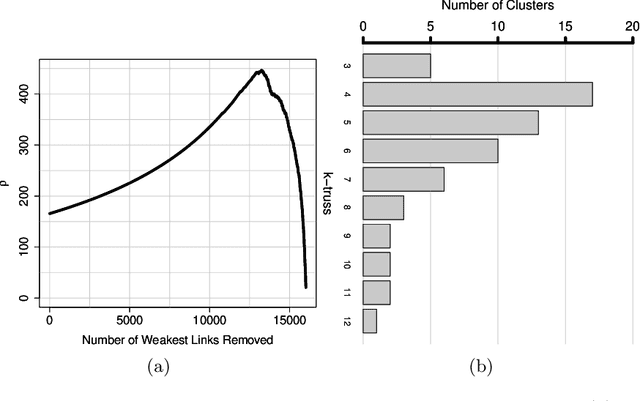
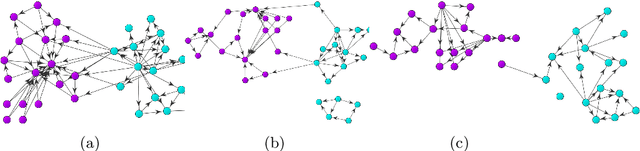
Abstract:We present a new metric of link cohesion for measuring the strength of edges in complex, highly connected graphs. Link cohesion accounts for local small hop connections and associated node degrees and can be used to support edge scoring and graph simplification. We also present a novel graph density measure to estimate the average cohesion across nodes. Link cohesion and the density measure are employed to demonstrate community detection through graph sparsification by maximizing graph density. Link cohesion is also shown to be loosely correlated with edge betweenness centrality.
GALILEO: A Generalized Low-Entropy Mixture Model
Aug 24, 2017

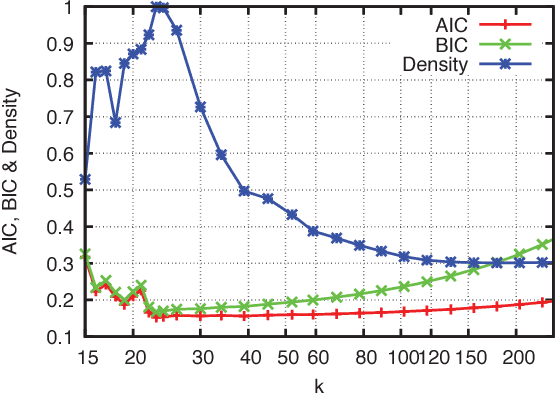
Abstract:We present a new method of generating mixture models for data with categorical attributes. The keys to this approach are an entropy-based density metric in categorical space and annealing of high-entropy/low-density components from an initial state with many components. Pruning of low-density components using the entropy-based density allows GALILEO to consistently find high-quality clusters and the same optimal number of clusters. GALILEO has shown promising results on a range of test datasets commonly used for categorical clustering benchmarks. We demonstrate that the scaling of GALILEO is linear in the number of records in the dataset, making this method suitable for very large categorical datasets.
* 7 pages, 8 figures, 3 tables
Bayesian Learning of Clique Tree Structure
Aug 23, 2017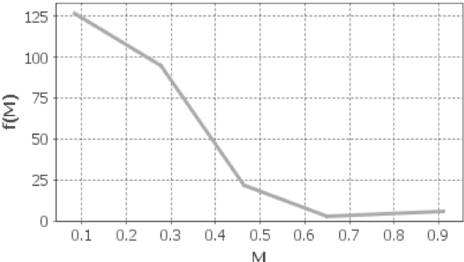

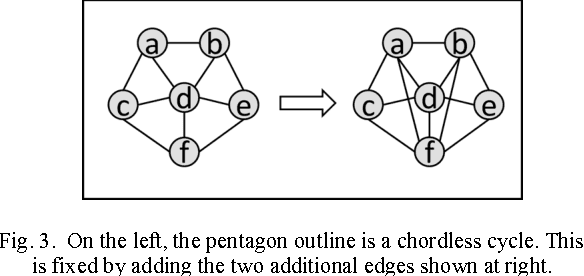
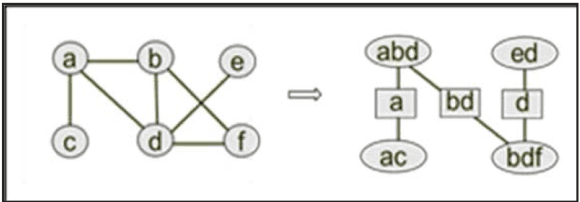
Abstract:The problem of categorical data analysis in high dimensions is considered. A discussion of the fundamental difficulties of probability modeling is provided, and a solution to the derivation of high dimensional probability distributions based on Bayesian learning of clique tree decomposition is presented. The main contributions of this paper are an automated determination of the optimal clique tree structure for probability modeling, the resulting derived probability distribution, and a corresponding unified approach to clustering and anomaly detection based on the probability distribution.
* 7 pages, 11 figures; see http://worldcomp-proceedings.com/proc/p2016/DMIN16_Contents.html
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge