Catherine Schwartz
Random Subspace Mixture Models for Interpretable Anomaly Detection
Aug 13, 2021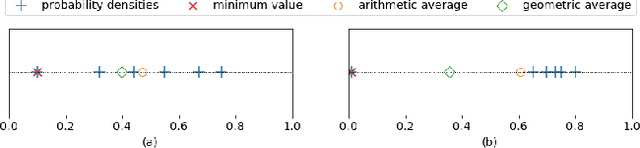
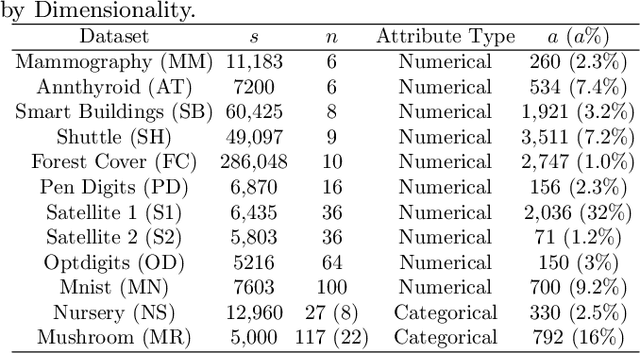
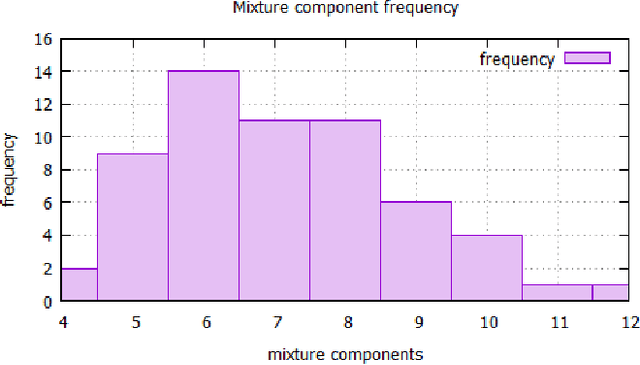
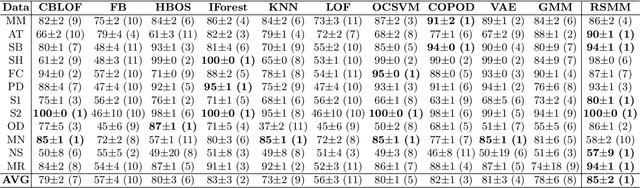
Abstract:We present a new subspace-based method to construct probabilistic models for high-dimensional data and highlight its use in anomaly detection. The approach is based on a statistical estimation of probability density using densities of random subspaces combined with geometric averaging. In selecting random subspaces, equal representation of each attribute is used to ensure correct statistical limits. Gaussian mixture models (GMMs) are used to create the probability densities for each subspace with techniques included to mitigate singularities allowing for the ability to handle both numerical and categorial attributes. The number of components for each GMM is determined automatically through Bayesian information criterion to prevent overfitting. The proposed algorithm attains competitive AUC scores compared with prominent algorithms against benchmark anomaly detection datasets with the added benefits of being simple, scalable, and interpretable.
* 10 pages
Novel Edge and Density Metrics for Link Cohesion
Mar 06, 2020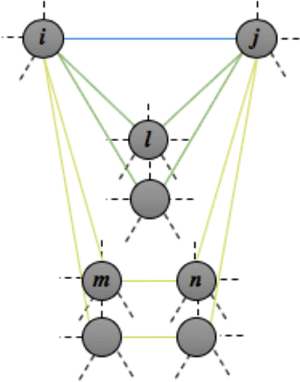
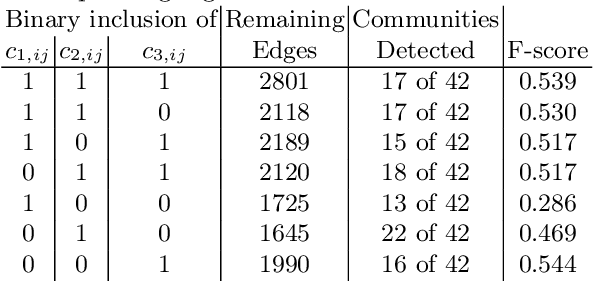
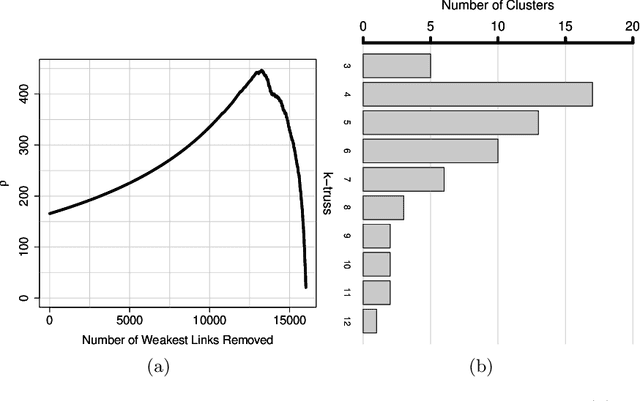
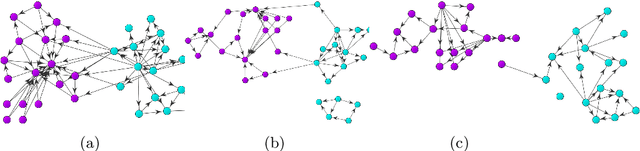
Abstract:We present a new metric of link cohesion for measuring the strength of edges in complex, highly connected graphs. Link cohesion accounts for local small hop connections and associated node degrees and can be used to support edge scoring and graph simplification. We also present a novel graph density measure to estimate the average cohesion across nodes. Link cohesion and the density measure are employed to demonstrate community detection through graph sparsification by maximizing graph density. Link cohesion is also shown to be loosely correlated with edge betweenness centrality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge