Alex Mansbridge
Learning to Noise: Application-Agnostic Data Sharing with Local Differential Privacy
Oct 23, 2020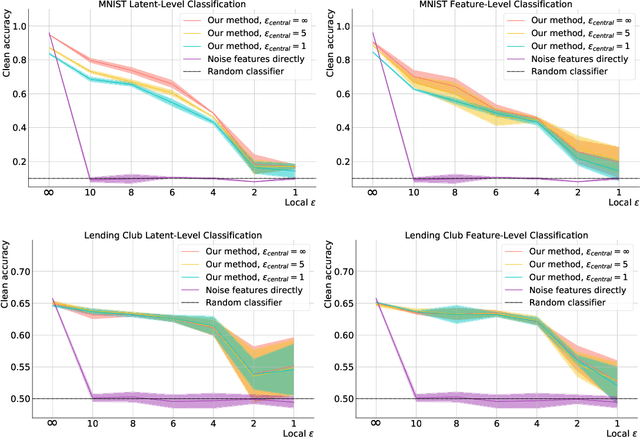
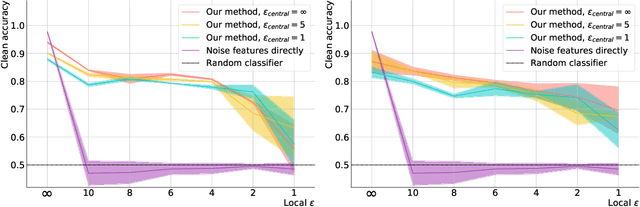
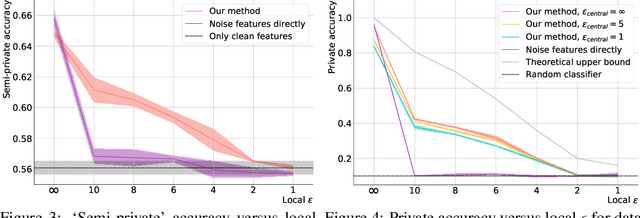
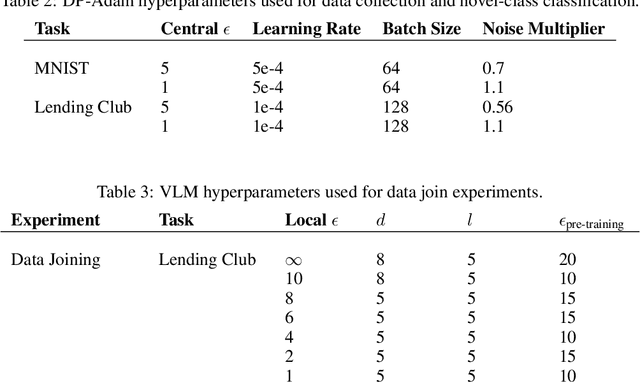
Abstract:In recent years, the collection and sharing of individuals' private data has become commonplace in many industries. Local differential privacy (LDP) is a rigorous approach which uses a randomized algorithm to preserve privacy even from the database administrator, unlike the more standard central differential privacy. For LDP, when applying noise directly to high-dimensional data, the level of noise required all but entirely destroys data utility. In this paper we introduce a novel, application-agnostic privatization mechanism that leverages representation learning to overcome the prohibitive noise requirements of direct methods, while maintaining the strict guarantees of LDP. We further demonstrate that this privatization mechanism can be used to train machine learning algorithms across a range of applications, including private data collection, private novel-class classification, and the augmentation of clean datasets with additional privatized features. We achieve significant gains in performance on downstream classification tasks relative to benchmarks that noise the data directly, which are state-of-the-art in the context of application-agnostic LDP mechanisms for high-dimensional data.
Improving latent variable descriptiveness with AutoGen
Jun 12, 2018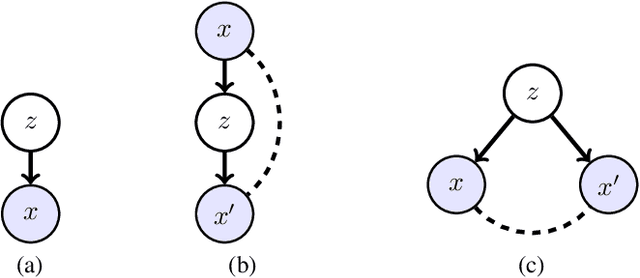

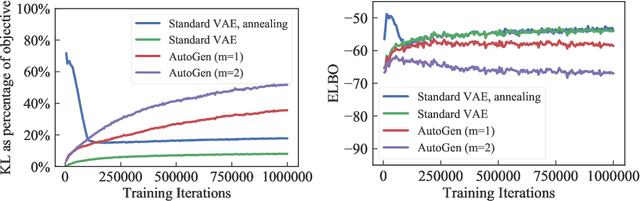

Abstract:Powerful generative models, particularly in Natural Language Modelling, are commonly trained by maximizing a variational lower bound on the data log likelihood. These models often suffer from poor use of their latent variable, with ad-hoc annealing factors used to encourage retention of information in the latent variable. We discuss an alternative and general approach to latent variable modelling, based on an objective that combines the data log likelihood as well as the likelihood of a perfect reconstruction through an autoencoder. Tying these together ensures by design that the latent variable captures information about the observations, whilst retaining the ability to generate well. Interestingly, though this approach is a priori unrelated to VAEs, the lower bound attained is identical to the standard VAE bound but with the addition of a simple pre-factor; thus, providing a formal interpretation of the commonly used, ad-hoc pre-factors in training VAEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge