Deep Learning Evidence for Global Optimality of Gerver's Sofa

The Moving Sofa Problem, formally proposed by Leo Moser in 1966, seeks to determine the largest area of a two-dimensional shape that can navigate through an $L$-shaped corridor with unit width. The current best lower bound is about 2.2195, achieved by Joseph Gerver in 1992, though its global optimality remains unproven. In this paper, we investigate this problem by leveraging the universal approximation strength and computational efficiency of neural networks. We report two approaches, both supporting Gerver's conjecture that his shape is the unique global maximum. Our first approach is continuous function learning. We drop Gerver's assumptions that i) the rotation of the corridor is monotonic and symmetric and, ii) the trajectory of its corner as a function of rotation is continuously differentiable. We parameterize rotation and trajectory by independent piecewise linear neural networks (with input being some pseudo time), allowing for rich movements such as backward rotation and pure translation. We then compute the sofa area as a differentiable function of rotation and trajectory using our "waterfall" algorithm. Our final loss function includes differential terms and initial conditions, leveraging the principles of physics-informed machine learning. Under such settings, extensive training starting from diverse function initialization and hyperparameters is conducted, unexceptionally showing rapid convergence to Gerver's solution. Our second approach is via discrete optimization of the Kallus-Romik upper bound, which converges to the maximum sofa area from above as the number of rotation angles increases. We uplift this number to 10000 to reveal its asymptotic behavior. It turns out that the upper bound yielded by our models does converge to Gerver's area (within an error of 0.01% when the number of angles reaches 2100). We also improve their five-angle upper bound from 2.37 to 2.3337.

Feature-Action Design Patterns for Storytelling Visualizations with Time Series Data

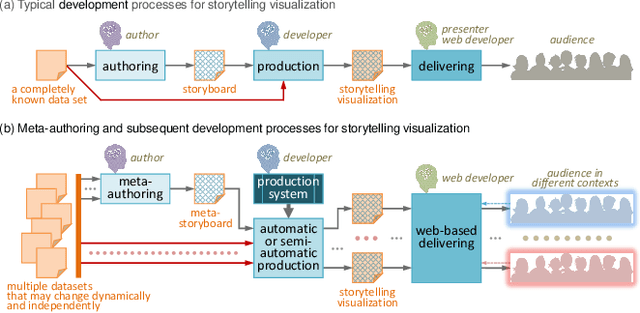
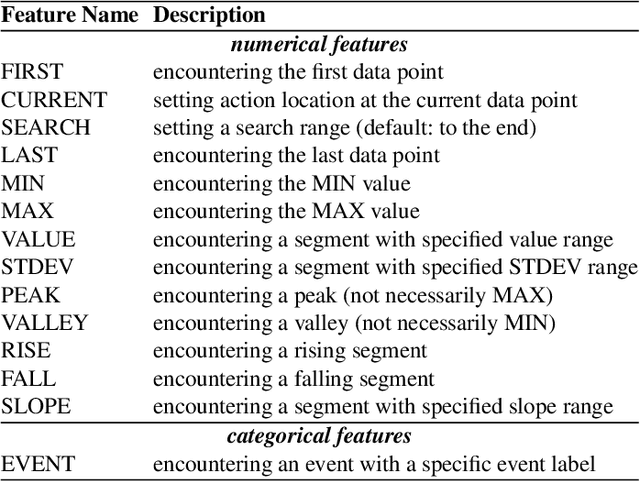
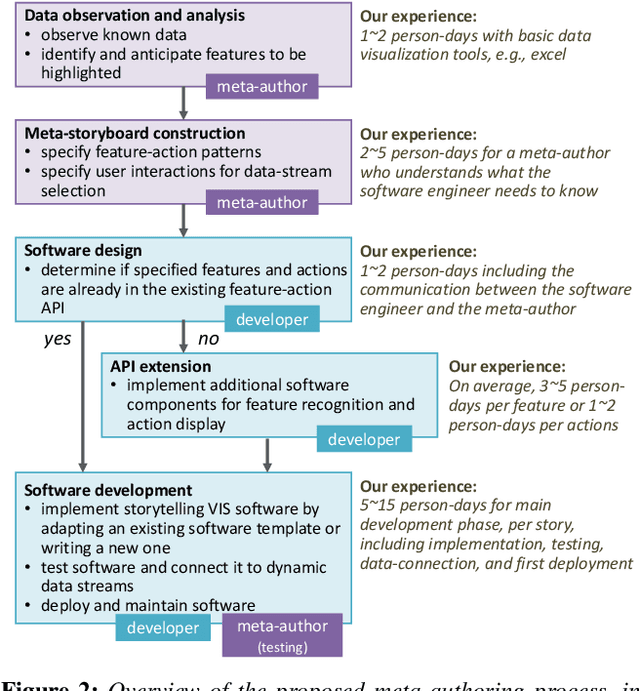
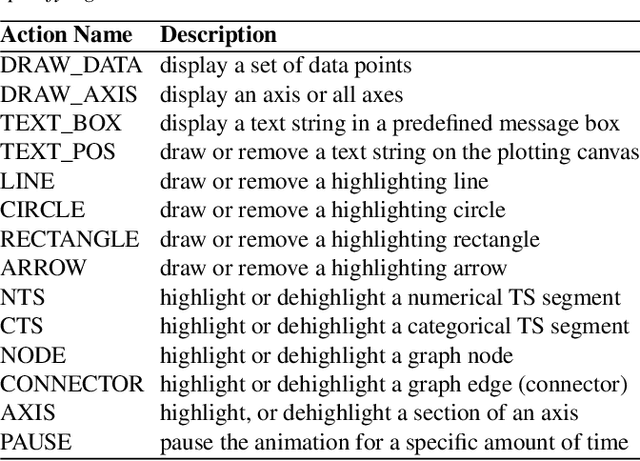
We present a method to create storytelling visualization with time series data. Many personal decisions nowadays rely on access to dynamic data regularly, as we have seen during the COVID-19 pandemic. It is thus desirable to construct storytelling visualization for dynamic data that is selected by an individual for a specific context. Because of the need to tell data-dependent stories, predefined storyboards based on known data cannot accommodate dynamic data easily nor scale up to many different individuals and contexts. Motivated initially by the need to communicate time series data during the COVID-19 pandemic, we developed a novel computer-assisted method for meta-authoring of stories, which enables the design of storyboards that include feature-action patterns in anticipation of potential features that may appear in dynamically arrived or selected data. In addition to meta-storyboards involving COVID-19 data, we also present storyboards for telling stories about progress in a machine learning workflow. Our approach is complementary to traditional methods for authoring storytelling visualization, and provides an efficient means to construct data-dependent storyboards for different data-streams of similar contexts.

Zero Coordinate Shift: Whetted Automatic Differentiation for Physics-informed Operator Learning

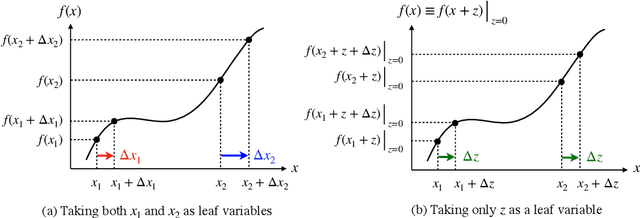
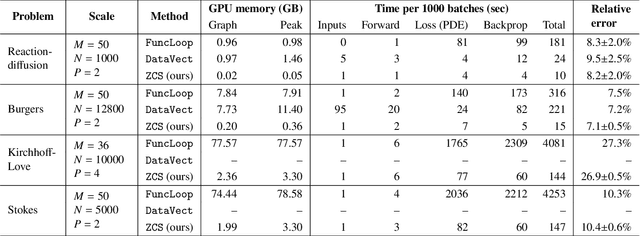
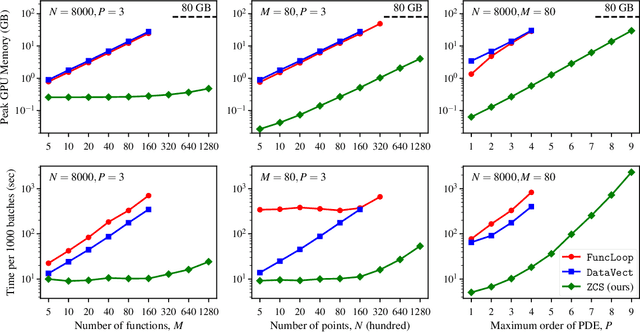
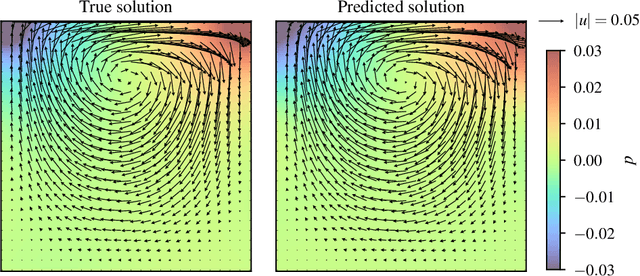
Automatic differentiation (AD) is a critical step in physics-informed machine learning, required for computing the high-order derivatives of network output w.r.t. coordinates. In this paper, we present a novel and lightweight algorithm to conduct such AD for physics-informed operator learning, as we call the trick of Zero Coordinate Shift (ZCS). Instead of making all sampled coordinates leaf variables, ZCS introduces only one scalar-valued leaf variable for each spatial or temporal dimension, leading to a game-changing performance leap by simplifying the wanted derivatives from "many-roots-many-leaves" to "one-root-many-leaves". ZCS is easy to implement with current deep learning libraries; our own implementation is by extending the DeepXDE package. We carry out a comprehensive benchmark analysis and several case studies, training physics-informed DeepONets to solve partial differential equations (PDEs) without data. The results show that ZCS has persistently brought down GPU memory consumption and wall time for training by an order of magnitude, with the savings increasing with problem scale (i.e., number of functions, number of points and order of PDE). As a low-level optimisation, ZCS entails no restrictions on data, physics (PDEs) or network architecture and does not compromise training results from any aspect.

Padding-free Convolution based on Preservation of Differential Characteristics of Kernels

Convolution is a fundamental operation in image processing and machine learning. Aimed primarily at maintaining image size, padding is a key ingredient of convolution, which, however, can introduce undesirable boundary effects. We present a non-padding-based method for size-keeping convolution based on the preservation of differential characteristics of kernels. The main idea is to make convolution over an incomplete sliding window "collapse" to a linear differential operator evaluated locally at its central pixel, which no longer requires information from the neighbouring missing pixels. While the underlying theory is rigorous, our final formula turns out to be simple: the convolution over an incomplete window is achieved by convolving its nearest complete window with a transformed kernel. This formula is computationally lightweight, involving neither interpolation or extrapolation nor restrictions on image and kernel sizes. Our method favours data with smooth boundaries, such as high-resolution images and fields from physics. Our experiments include: i) filtering analytical and non-analytical fields from computational physics and, ii) training convolutional neural networks (CNNs) for the tasks of image classification, semantic segmentation and super-resolution reconstruction. In all these experiments, our method has exhibited visible superiority over the compared ones.

On the Compatibility between a Neural Network and a Partial Differential Equation for Physics-informed Learning

We shed light on a pitfall and an opportunity in physics-informed neural networks (PINNs). We prove that a multilayer perceptron (MLP) only with ReLU (Rectified Linear Unit) or ReLU-like Lipschitz activation functions will always lead to a vanished Hessian. Such a network-imposed constraint contradicts any second- or higher-order partial differential equations (PDEs). Therefore, a ReLU-based MLP cannot form a permissible function space for the approximation of their solutions. Inspired by this pitfall, we prove that a linear PDE up to the $n$-th order can be strictly satisfied by an MLP with $C^n$ activation functions when the weights of its output layer lie on a certain hyperplane, as called the out-layer-hyperplane. An MLP equipped with the out-layer-hyperplane becomes "physics-enforced", no longer requiring a loss function for the PDE itself (but only those for the initial and boundary conditions). Such a hyperplane exists not only for MLPs but for any network architecture tailed by a fully-connected hidden layer. To our knowledge, this should be the first PINN architecture that enforces point-wise correctness of a PDE. We give the closed-form expression of the out-layer-hyperplane for second-order linear PDEs and provide an implementation.

Affinity-VAE for disentanglement, clustering and classification of objects in multidimensional image data

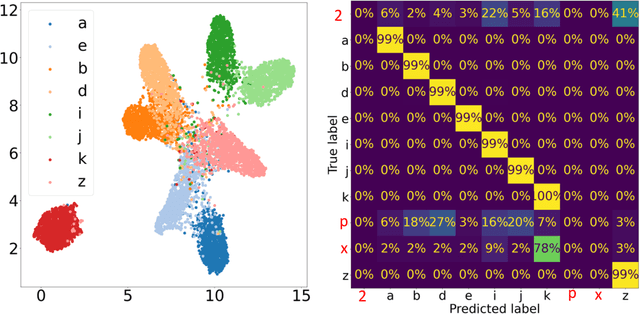
In this work we present affinity-VAE: a framework for automatic clustering and classification of objects in multidimensional image data based on their similarity. The method expands on the concept of $\beta$-VAEs with an informed similarity-based loss component driven by an affinity matrix. The affinity-VAE is able to create rotationally-invariant, morphologically homogeneous clusters in the latent representation, with improved cluster separation compared with a standard $\beta$-VAE. We explore the extent of latent disentanglement and continuity of the latent spaces on both 2D and 3D image data, including simulated biological electron cryo-tomography (cryo-ET) volumes as an example of a scientific application.

Discovering the building blocks of dark matter halo density profiles with neural networks

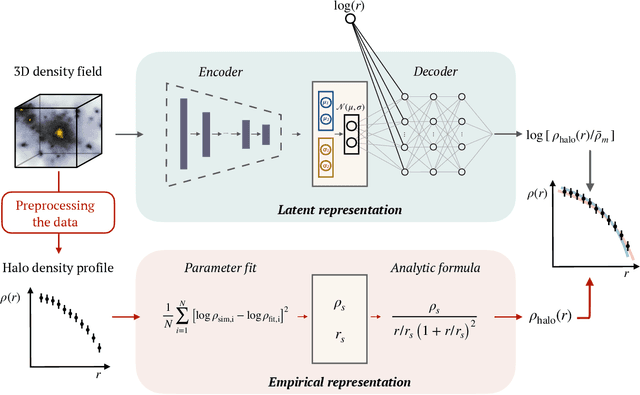
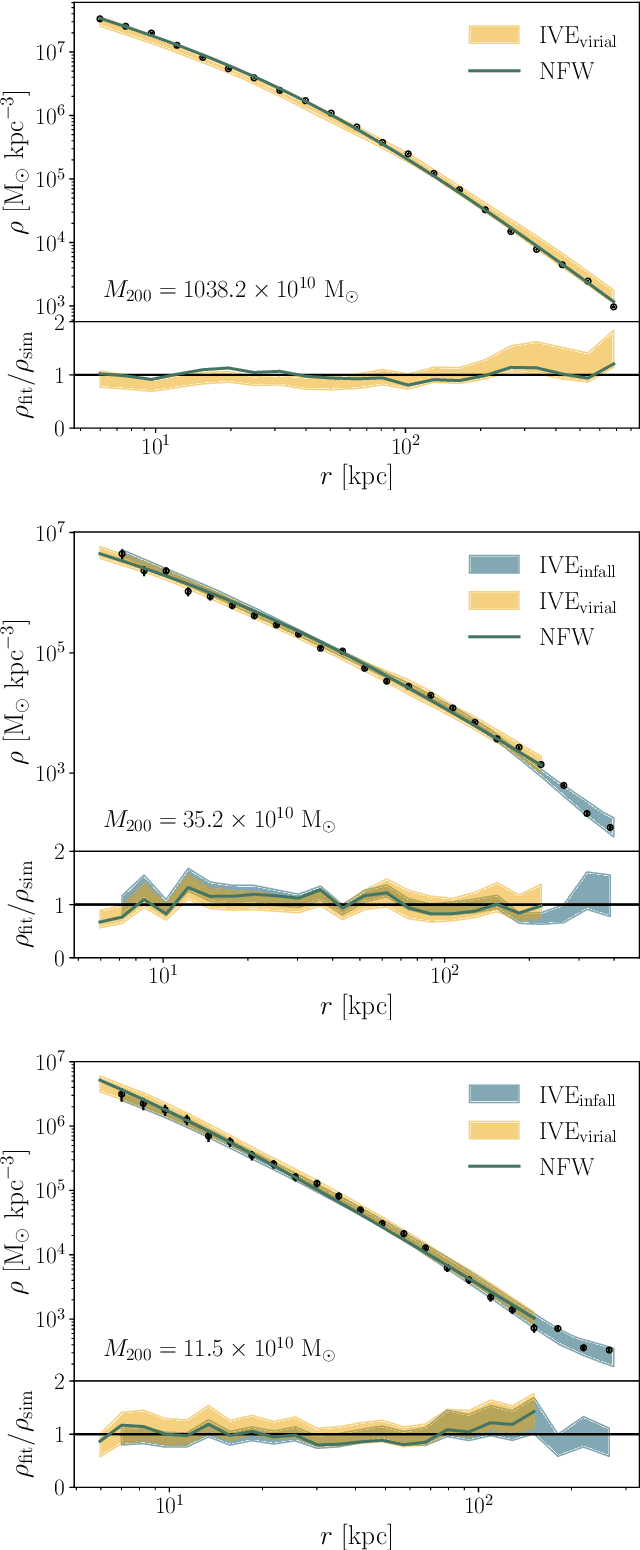
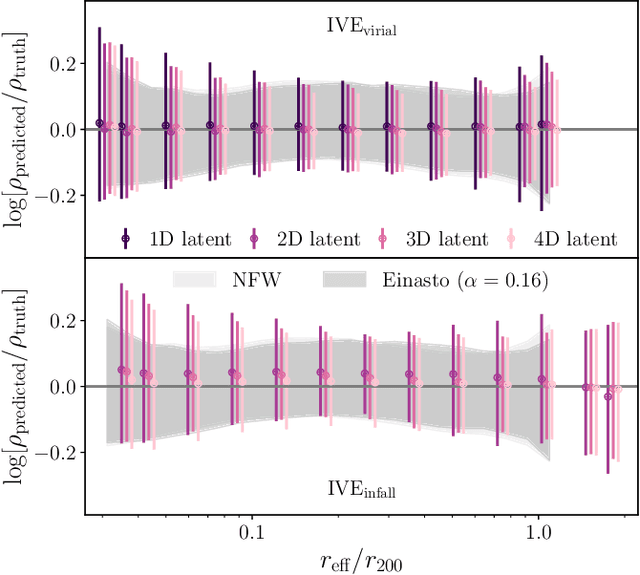
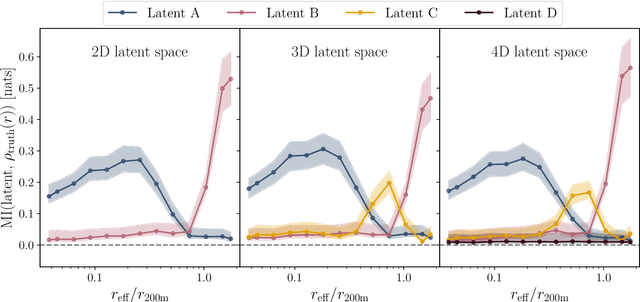
The density profiles of dark matter halos are typically modeled using empirical formulae fitted to the density profiles of relaxed halo populations. We present a neural network model that is trained to learn the mapping from the raw density field containing each halo to the dark matter density profile. We show that the model recovers the widely-used Navarro-Frenk-White (NFW) profile out to the virial radius, and can additionally describe the variability in the outer profile of the halos. The neural network architecture consists of a supervised encoder-decoder framework, which first compresses the density inputs into a low-dimensional latent representation, and then outputs $\rho(r)$ for any desired value of radius $r$. The latent representation contains all the information used by the model to predict the density profiles. This allows us to interpret the latent representation by quantifying the mutual information between the representation and the halos' ground-truth density profiles. A two-dimensional representation is sufficient to accurately model the density profiles up to the virial radius; however, a three-dimensional representation is required to describe the outer profiles beyond the virial radius. The additional dimension in the representation contains information about the infalling material in the outer profiles of dark matter halos, thus discovering the splashback boundary of halos without prior knowledge of the halos' dynamical history.

Disentangling Autoencoders (DAE)

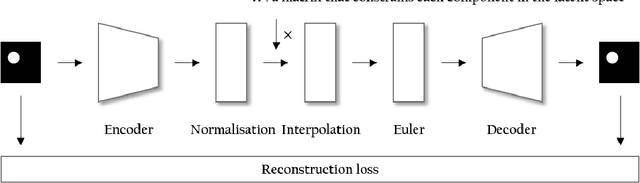
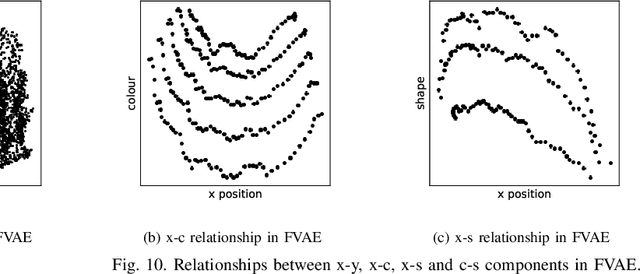
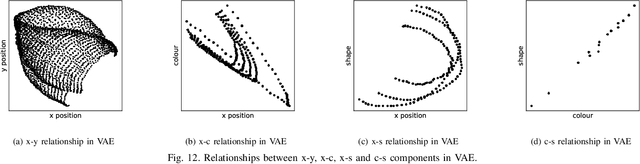
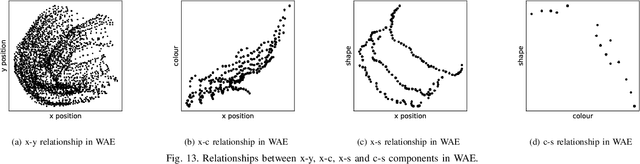
Noting the importance of factorizing or disentangling the latent space, we propose a novel framework for autoencoders based on the principles of symmetry transformations in group-theory, which is a non-probabilistic disentangling autoencoder model. To the best of our knowledge, this is the first model that is aiming to achieve disentanglement based on autoencoders without regularizers. The proposed model is compared to seven state-of-the-art generative models based on autoencoders and evaluated based on reconstruction loss and five metrics quantifying disentanglement losses. The experiment results show that the proposed model can have better disentanglement when variances of each features are different. We believe that this model leads a new field for disentanglement learning based on autoencoders without regularizers.

Scientific Machine Learning Benchmarks

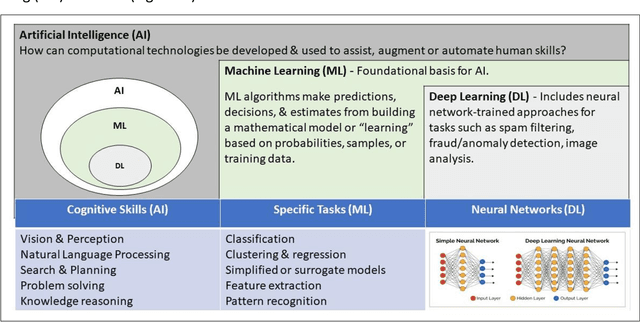
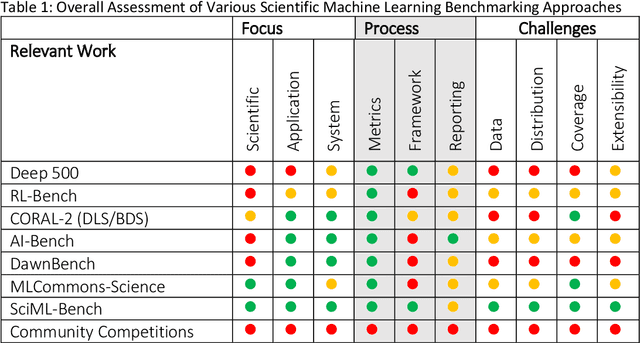
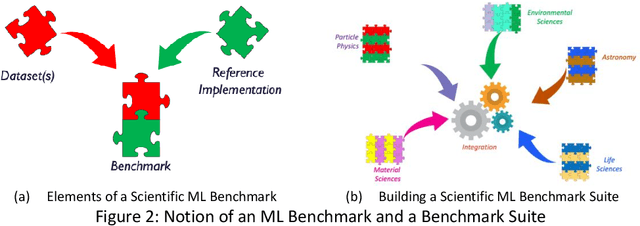
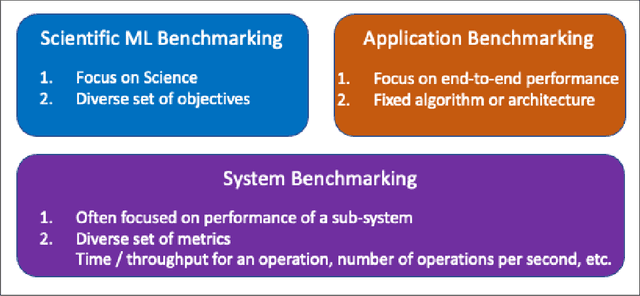
The breakthrough in Deep Learning neural networks has transformed the use of AI and machine learning technologies for the analysis of very large experimental datasets. These datasets are typically generated by large-scale experimental facilities at national laboratories. In the context of science, scientific machine learning focuses on training machines to identify patterns, trends, and anomalies to extract meaningful scientific insights from such datasets. With a new generation of experimental facilities, the rate of data generation and the scale of data volumes will increasingly require the use of more automated data analysis. At present, identifying the most appropriate machine learning algorithm for the analysis of any given scientific dataset is still a challenge for scientists. This is due to many different machine learning frameworks, computer architectures, and machine learning models. Historically, for modelling and simulation on HPC systems such problems have been addressed through benchmarking computer applications, algorithms, and architectures. Extending such a benchmarking approach and identifying metrics for the application of machine learning methods to scientific datasets is a new challenge for both scientists and computer scientists. In this paper, we describe our approach to the development of scientific machine learning benchmarks and review other approaches to benchmarking scientific machine learning.

Deep learning insights into cosmological structure formation

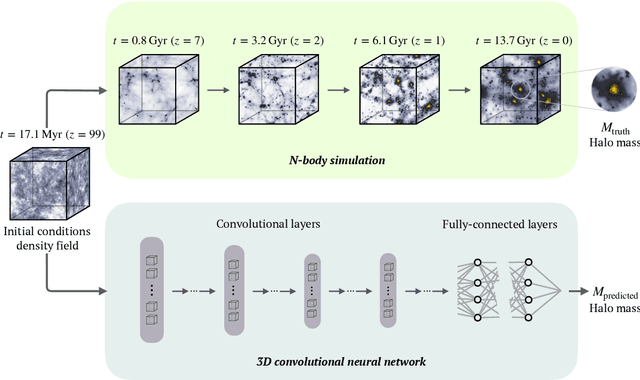
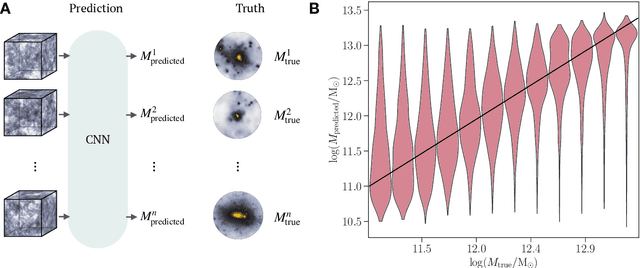
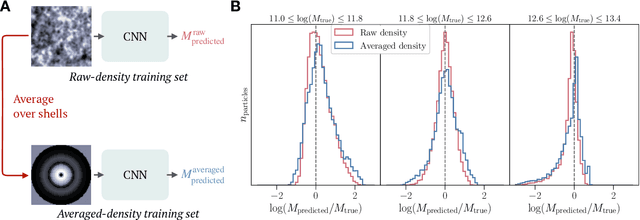
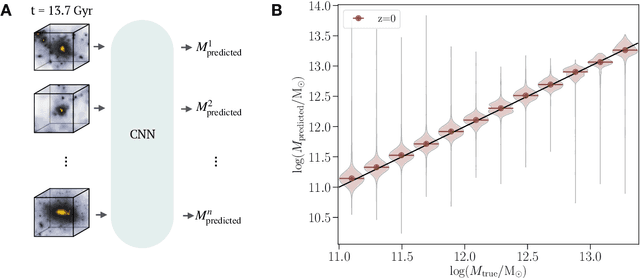
While the evolution of linear initial conditions present in the early universe into extended halos of dark matter at late times can be computed using cosmological simulations, a theoretical understanding of this complex process remains elusive. Here, we build a deep learning framework to learn this non-linear relationship, and develop techniques to physically interpret the learnt mapping. A three-dimensional convolutional neural network (CNN) is trained to predict the mass of dark matter halos from the initial conditions. We find no change in the predictive accuracy of the model if we retrain the model removing anisotropic information from the inputs. This suggests that the features learnt by the CNN are equivalent to spherical averages over the initial conditions. Our results indicate that interpretable deep learning frameworks can provide a powerful tool for extracting insight into cosmological structure formation.