Deep Learning Evidence for Global Optimality of Gerver's Sofa

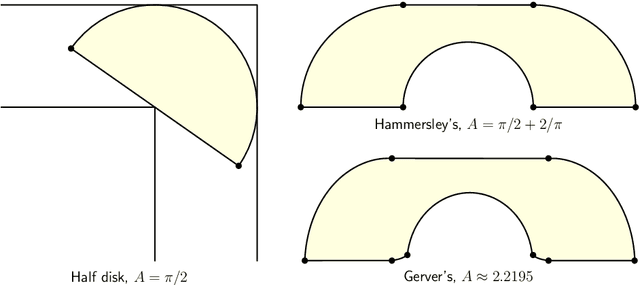
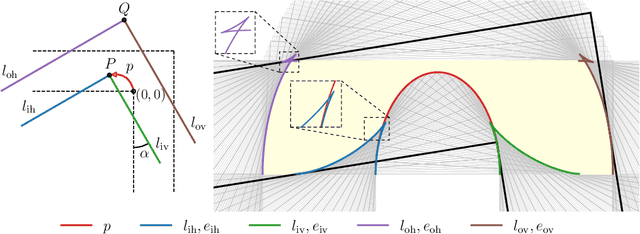
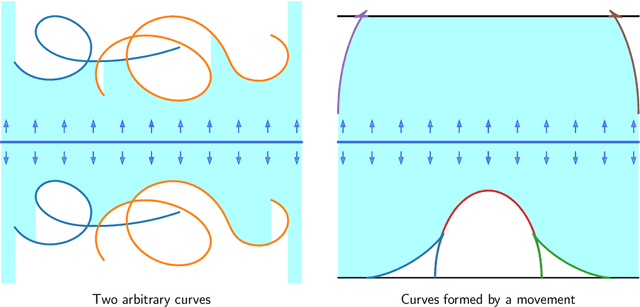
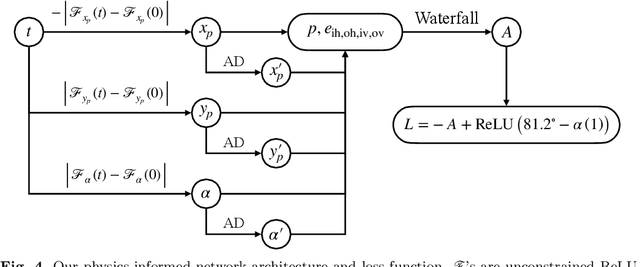
The Moving Sofa Problem, formally proposed by Leo Moser in 1966, seeks to determine the largest area of a two-dimensional shape that can navigate through an $L$-shaped corridor with unit width. The current best lower bound is about 2.2195, achieved by Joseph Gerver in 1992, though its global optimality remains unproven. In this paper, we investigate this problem by leveraging the universal approximation strength and computational efficiency of neural networks. We report two approaches, both supporting Gerver's conjecture that his shape is the unique global maximum. Our first approach is continuous function learning. We drop Gerver's assumptions that i) the rotation of the corridor is monotonic and symmetric and, ii) the trajectory of its corner as a function of rotation is continuously differentiable. We parameterize rotation and trajectory by independent piecewise linear neural networks (with input being some pseudo time), allowing for rich movements such as backward rotation and pure translation. We then compute the sofa area as a differentiable function of rotation and trajectory using our "waterfall" algorithm. Our final loss function includes differential terms and initial conditions, leveraging the principles of physics-informed machine learning. Under such settings, extensive training starting from diverse function initialization and hyperparameters is conducted, unexceptionally showing rapid convergence to Gerver's solution. Our second approach is via discrete optimization of the Kallus-Romik upper bound, which converges to the maximum sofa area from above as the number of rotation angles increases. We uplift this number to 10000 to reveal its asymptotic behavior. It turns out that the upper bound yielded by our models does converge to Gerver's area (within an error of 0.01% when the number of angles reaches 2100). We also improve their five-angle upper bound from 2.37 to 2.3337.

GhostShiftAddNet: More Features from Energy-Efficient Operations

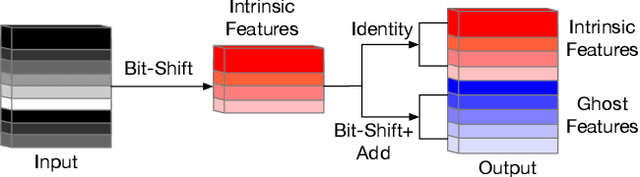
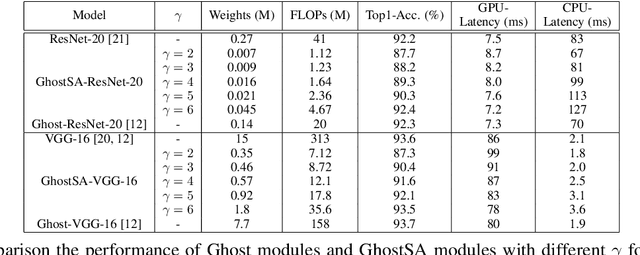
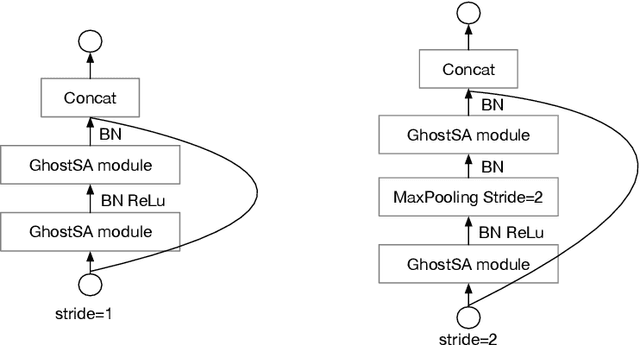
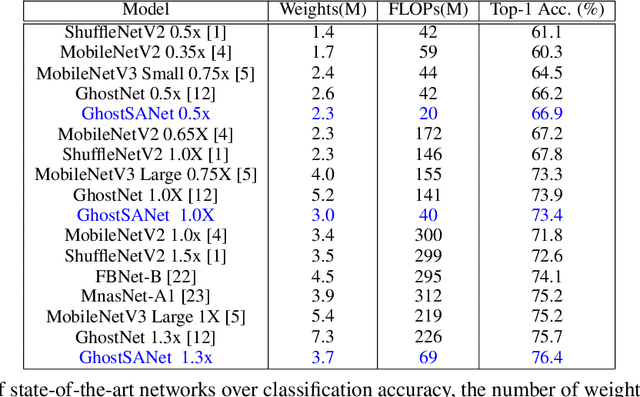
Deep convolutional neural networks (CNNs) are computationally and memory intensive. In CNNs, intensive multiplication can have resource implications that may challenge the ability for effective deployment of inference on resource-constrained edge devices. This paper proposes GhostShiftAddNet, where the motivation is to implement a hardware-efficient deep network: a multiplication-free CNN with fewer redundant features. We introduce a new bottleneck block, GhostSA, that converts all multiplications in the block to cheap operations. The bottleneck uses an appropriate number of bit-shift filters to process intrinsic feature maps, then applies a series of transformations that consist of bit-wise shifts with addition operations to generate more feature maps that fully learn to capture information underlying intrinsic features. We schedule the number of bit-shift and addition operations for different hardware platforms. We conduct extensive experiments and ablation studies with desktop and embedded (Jetson Nano) devices for implementation and measurements. We demonstrate the proposed GhostSA block can replace bottleneck blocks in the backbone of state-of-the-art networks architectures and gives improved performance on image classification benchmarks. Further, our GhostShiftAddNet can achieve higher classification accuracy with fewer FLOPs and parameters (reduced by up to 3x) than GhostNet. When compared to GhostNet, inference latency on the Jetson Nano is improved by 1.3x and 2x on the GPU and CPU respectively.

Dynamic Transformer for Efficient Machine Translation on Embedded Devices

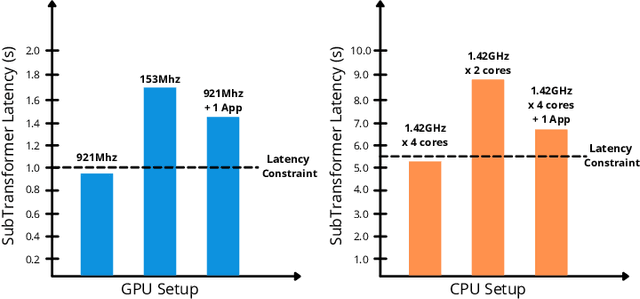
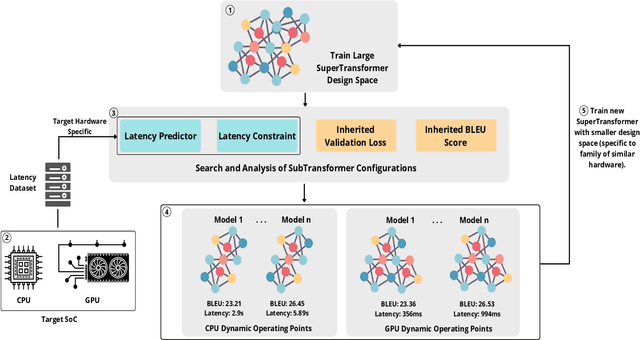
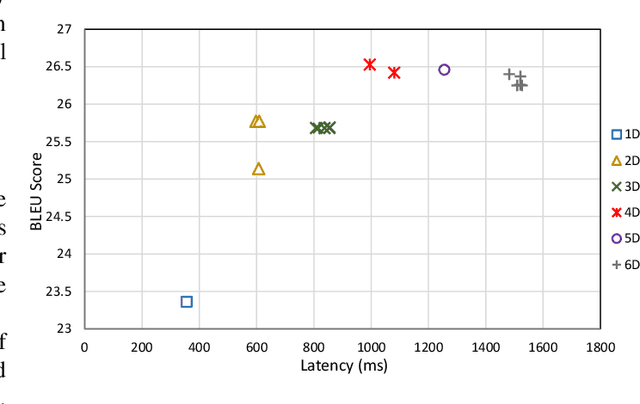
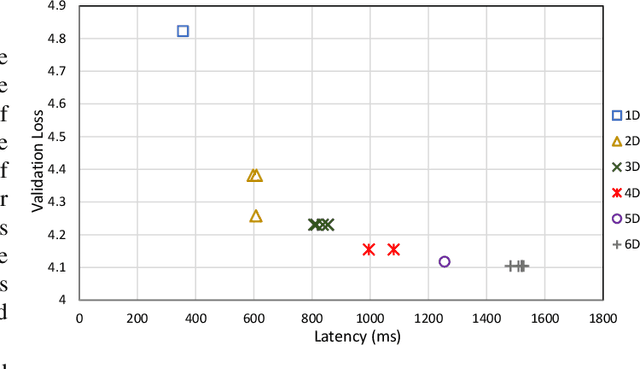
The Transformer architecture is widely used for machine translation tasks. However, its resource-intensive nature makes it challenging to implement on constrained embedded devices, particularly where available hardware resources can vary at run-time. We propose a dynamic machine translation model that scales the Transformer architecture based on the available resources at any particular time. The proposed approach, 'Dynamic-HAT', uses a HAT SuperTransformer as the backbone to search for SubTransformers with different accuracy-latency trade-offs at design time. The optimal SubTransformers are sampled from the SuperTransformer at run-time, depending on latency constraints. The Dynamic-HAT is tested on the Jetson Nano and the approach uses inherited SubTransformers sampled directly from the SuperTransformer with a switching time of <1s. Using inherited SubTransformers results in a BLEU score loss of <1.5% because the SubTransformer configuration is not retrained from scratch after sampling. However, to recover this loss in performance, the dimensions of the design space can be reduced to tailor it to a family of target hardware. The new reduced design space results in a BLEU score increase of approximately 1% for sub-optimal models from the original design space, with a wide range for performance scaling between 0.356s - 1.526s for the GPU and 2.9s - 7.31s for the CPU.

Dynamic-OFA: Runtime DNN Architecture Switching for Performance Scaling on Heterogeneous Embedded Platforms

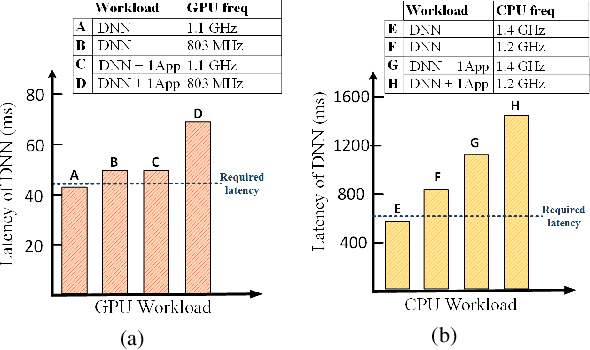
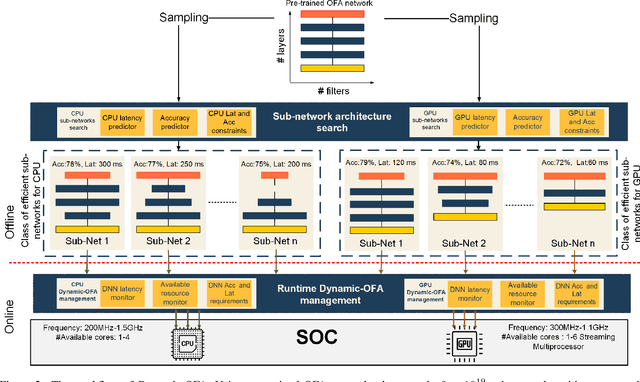
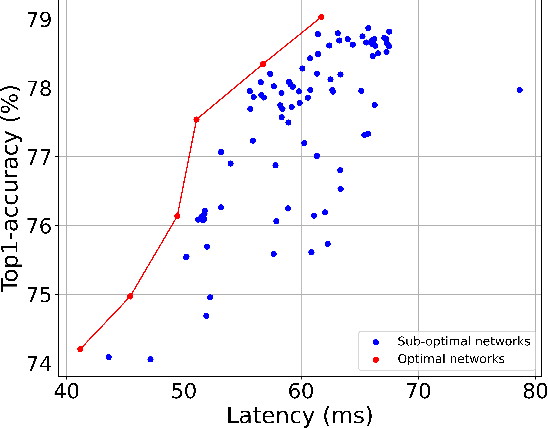
Mobile and embedded platforms are increasingly required to efficiently execute computationally demanding DNNs across heterogeneous processing elements. At runtime, the available hardware resources to DNNs can vary considerably due to other concurrently running applications. The performance requirements of the applications could also change under different scenarios. To achieve the desired performance, dynamic DNNs have been proposed in which the number of channels/layers can be scaled in real time to meet different requirements under varying resource constraints. However, the training process of such dynamic DNNs can be costly, since platform-aware models of different deployment scenarios must be retrained to become dynamic. This paper proposes Dynamic-OFA, a novel dynamic DNN approach for state-of-the-art platform-aware NAS models (i.e. Once-for-all network (OFA)). Dynamic-OFA pre-samples a family of sub-networks from a static OFA backbone model, and contains a runtime manager to choose different sub-networks under different runtime environments. As such, Dynamic-OFA does not need the traditional dynamic DNN training pipeline. Compared to the state-of-the-art, our experimental results using ImageNet on a Jetson Xavier NX show that the approach is up to 3.5x (CPU), 2.4x (GPU) faster for similar ImageNet Top-1 accuracy, or 3.8% (CPU), 5.1% (GPU) higher accuracy at similar latency.

A Variance Controlled Stochastic Method with Biased Estimation for Faster Non-convex Optimization

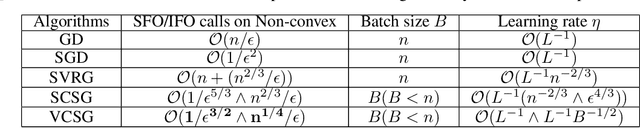
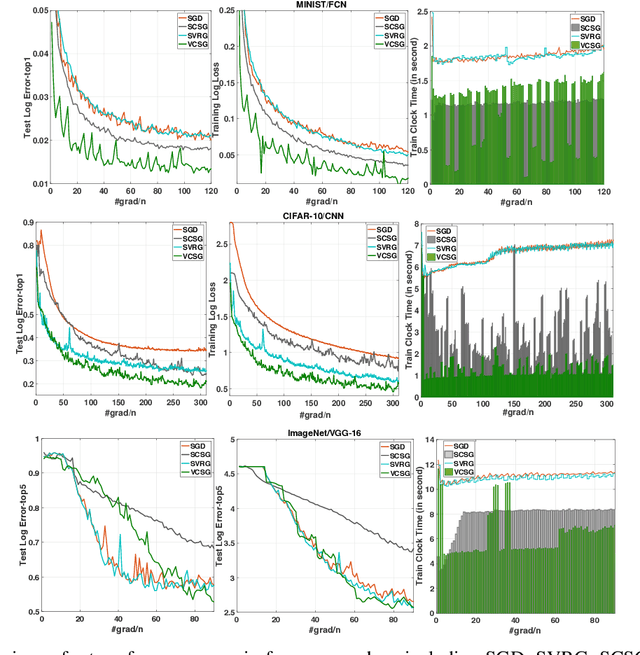
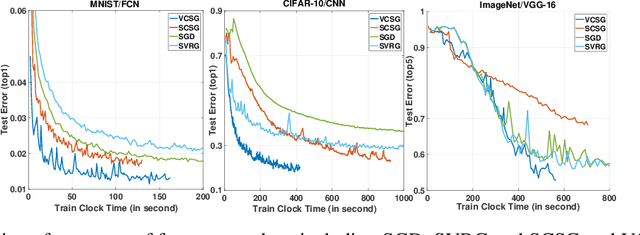
In this paper, we proposed a new technique, {\em variance controlled stochastic gradient} (VCSG), to improve the performance of the stochastic variance reduced gradient (SVRG) algorithm. To avoid over-reducing the variance of gradient by SVRG, a hyper-parameter $\lambda$ is introduced in VCSG that is able to control the reduced variance of SVRG. Theory shows that the optimization method can converge by using an unbiased gradient estimator, but in practice, biased gradient estimation can allow more efficient convergence to the vicinity since an unbiased approach is computationally more expensive. $\lambda$ also has the effect of balancing the trade-off between unbiased and biased estimations. Secondly, to minimize the number of full gradient calculations in SVRG, a variance-bounded batch is introduced to reduce the number of gradient calculations required in each iteration. For smooth non-convex functions, the proposed algorithm converges to an approximate first-order stationary point (i.e. $\mathbb{E}\|\nabla{f}(x)\|^{2}\leq\epsilon$) within $\mathcal{O}(min\{1/\epsilon^{3/2},n^{1/4}/\epsilon\})$ number of stochastic gradient evaluations, which improves the leading gradient complexity of stochastic gradient-based method SCS $(\mathcal{O}(min\{1/\epsilon^{5/3},n^{2/3}/\epsilon\})$. It is shown theoretically and experimentally that VCSG can be deployed to improve convergence.

A Stochastic Gradient Method with Biased Estimation for Faster Nonconvex Optimization

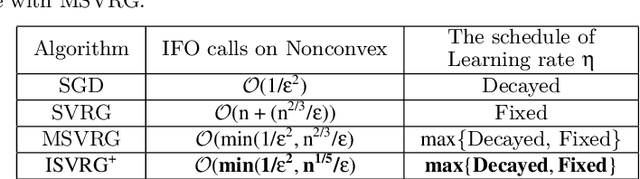
A number of optimization approaches have been proposed for optimizing nonconvex objectives (e.g. deep learning models), such as batch gradient descent, stochastic gradient descent and stochastic variance reduced gradient descent. Theory shows these optimization methods can converge by using an unbiased gradient estimator. However, in practice biased gradient estimation can allow more efficient convergence to the vicinity since an unbiased approach is computationally more expensive. To produce fast convergence there are two trade-offs of these optimization strategies which are between stochastic/batch, and between biased/unbiased. This paper proposes an integrated approach which can control the nature of the stochastic element in the optimizer and can balance the trade-off of estimator between the biased and unbiased by using a hyper-parameter. It is shown theoretically and experimentally that this hyper-parameter can be configured to provide an effective balance to improve the convergence rate.