Deep Learning Evidence for Global Optimality of Gerver's Sofa

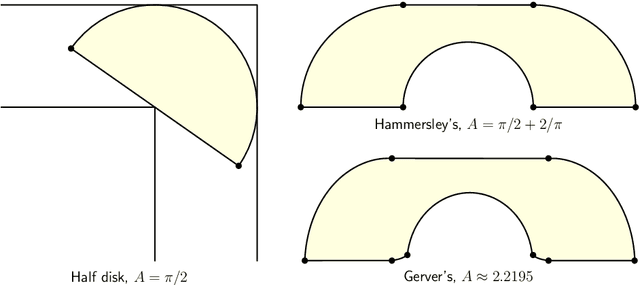
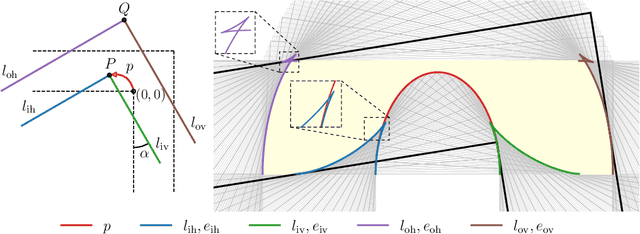
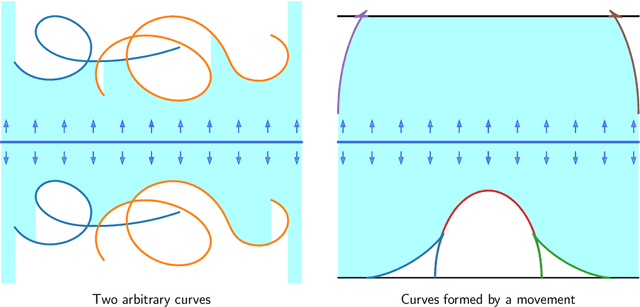
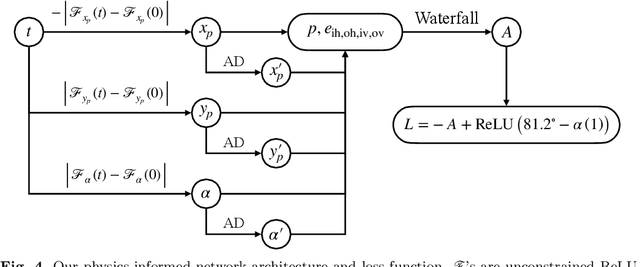
The Moving Sofa Problem, formally proposed by Leo Moser in 1966, seeks to determine the largest area of a two-dimensional shape that can navigate through an $L$-shaped corridor with unit width. The current best lower bound is about 2.2195, achieved by Joseph Gerver in 1992, though its global optimality remains unproven. In this paper, we investigate this problem by leveraging the universal approximation strength and computational efficiency of neural networks. We report two approaches, both supporting Gerver's conjecture that his shape is the unique global maximum. Our first approach is continuous function learning. We drop Gerver's assumptions that i) the rotation of the corridor is monotonic and symmetric and, ii) the trajectory of its corner as a function of rotation is continuously differentiable. We parameterize rotation and trajectory by independent piecewise linear neural networks (with input being some pseudo time), allowing for rich movements such as backward rotation and pure translation. We then compute the sofa area as a differentiable function of rotation and trajectory using our "waterfall" algorithm. Our final loss function includes differential terms and initial conditions, leveraging the principles of physics-informed machine learning. Under such settings, extensive training starting from diverse function initialization and hyperparameters is conducted, unexceptionally showing rapid convergence to Gerver's solution. Our second approach is via discrete optimization of the Kallus-Romik upper bound, which converges to the maximum sofa area from above as the number of rotation angles increases. We uplift this number to 10000 to reveal its asymptotic behavior. It turns out that the upper bound yielded by our models does converge to Gerver's area (within an error of 0.01% when the number of angles reaches 2100). We also improve their five-angle upper bound from 2.37 to 2.3337.

Feature-Action Design Patterns for Storytelling Visualizations with Time Series Data

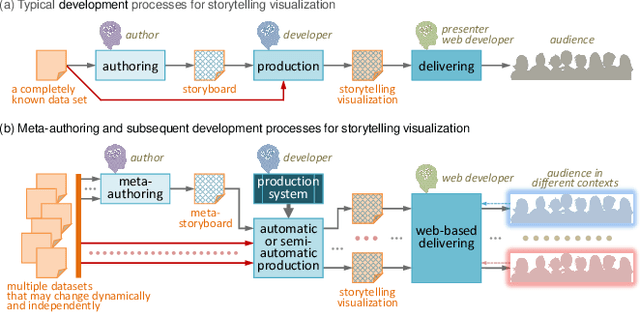
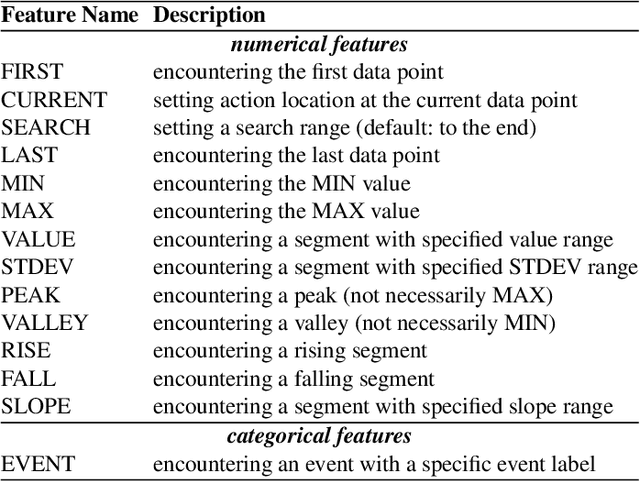
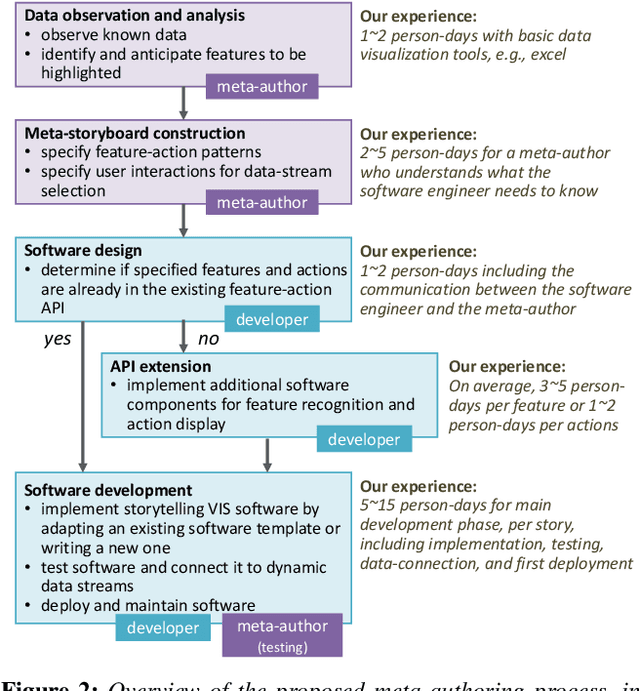
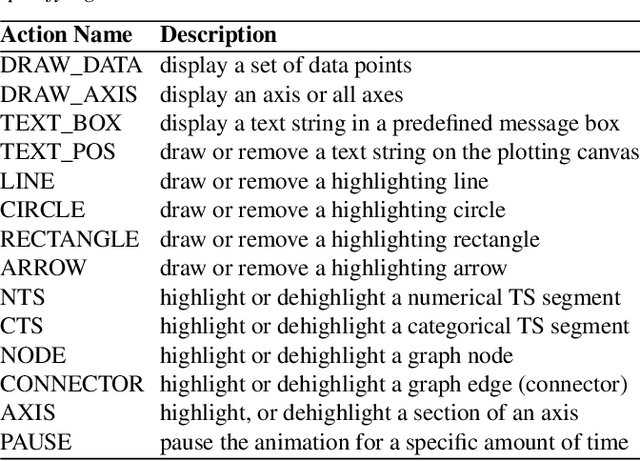
We present a method to create storytelling visualization with time series data. Many personal decisions nowadays rely on access to dynamic data regularly, as we have seen during the COVID-19 pandemic. It is thus desirable to construct storytelling visualization for dynamic data that is selected by an individual for a specific context. Because of the need to tell data-dependent stories, predefined storyboards based on known data cannot accommodate dynamic data easily nor scale up to many different individuals and contexts. Motivated initially by the need to communicate time series data during the COVID-19 pandemic, we developed a novel computer-assisted method for meta-authoring of stories, which enables the design of storyboards that include feature-action patterns in anticipation of potential features that may appear in dynamically arrived or selected data. In addition to meta-storyboards involving COVID-19 data, we also present storyboards for telling stories about progress in a machine learning workflow. Our approach is complementary to traditional methods for authoring storytelling visualization, and provides an efficient means to construct data-dependent storyboards for different data-streams of similar contexts.

Disentangling Autoencoders (DAE)

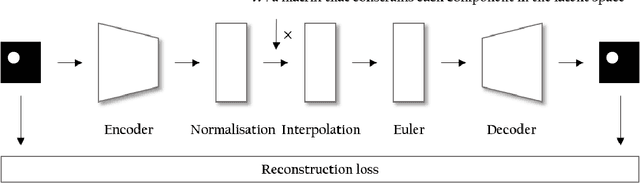
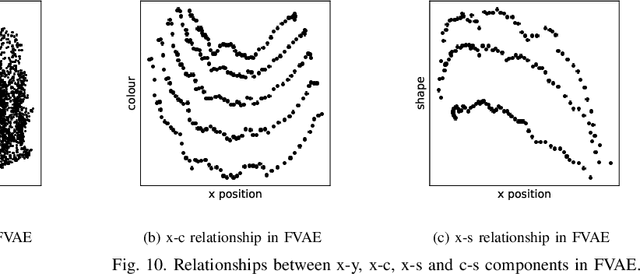
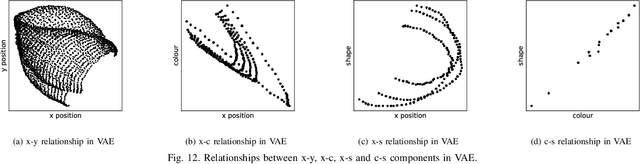
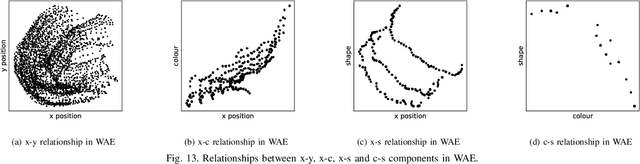
Noting the importance of factorizing or disentangling the latent space, we propose a novel framework for autoencoders based on the principles of symmetry transformations in group-theory, which is a non-probabilistic disentangling autoencoder model. To the best of our knowledge, this is the first model that is aiming to achieve disentanglement based on autoencoders without regularizers. The proposed model is compared to seven state-of-the-art generative models based on autoencoders and evaluated based on reconstruction loss and five metrics quantifying disentanglement losses. The experiment results show that the proposed model can have better disentanglement when variances of each features are different. We believe that this model leads a new field for disentanglement learning based on autoencoders without regularizers.

Hierarchical Auxiliary Learning

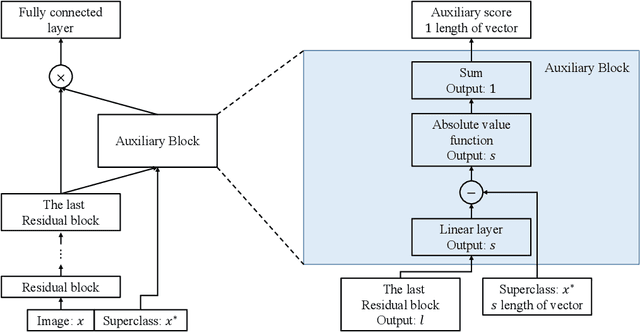
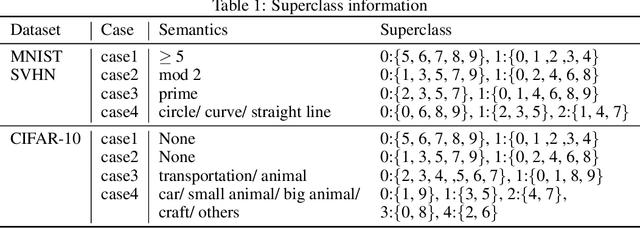
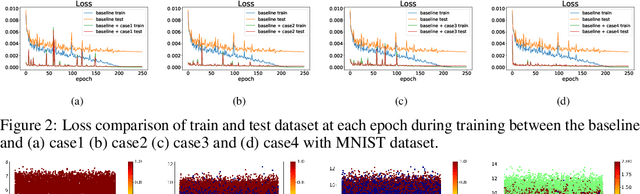
Conventional application of convolutional neural networks (CNNs) for image classification and recognition is based on the assumption that all target classes are equal(i.e., no hierarchy) and exclusive of one another (i.e., no overlap). CNN-based image classifiers built on this assumption, therefore, cannot take into account an innate hierarchy among target classes (e.g., cats and dogs in animal image classification) or additional information that can be easily derived from the data (e.g.,numbers larger than five in the recognition of handwritten digits), thereby resulting in scalability issues when the number of target classes is large. Combining two related but slightly different ideas of hierarchical classification and logical learning by auxiliary inputs, we propose a new learning framework called hierarchical auxiliary learning, which not only address the scalability issues with a large number of classes but also could further reduce the classification/recognition errors with a reasonable number of classes. In the hierarchical auxiliary learning, target classes are semantically or non-semantically grouped into superclasses, which turns the original problem of mapping between an image and its target class into a new problem of mapping between a pair of an image and its superclass and the target class. To take the advantage of superclasses, we introduce an auxiliary block into a neural network, which generates auxiliary scores used as additional information for final classification/recognition; in this paper, we add the auxiliary block between the last residual block and the fully-connected output layer of the ResNet. Experimental results demonstrate that the proposed hierarchical auxiliary learning can reduce classification errors up to 0.56, 1.6 and 3.56 percent with MNIST, SVHN and CIFAR-10 datasets, respectively.

On the Transformation of Latent Space in Autoencoders

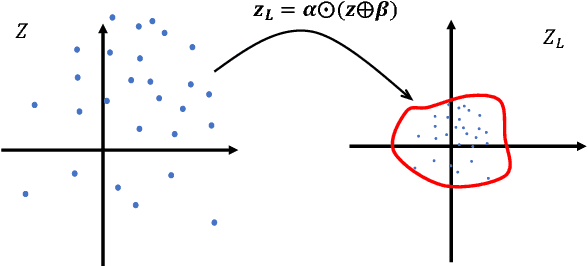
Noting the importance of the latent variables in inference and learning, we propose a novel framework for autoencoders based on the homeomorphic transformation of latent variables --- which could reduce the distance between vectors in the transformed space, while preserving the topological properties of the original space --- and investigate the effect of the transformation in both learning generative models and denoising corrupted data. The results of our experiments show that the proposed model can work as both a generative model and a denoising model with improved performance due to the transformation compared to conventional variational and denoising autoencoders.