Deep Learning Evidence for Global Optimality of Gerver's Sofa

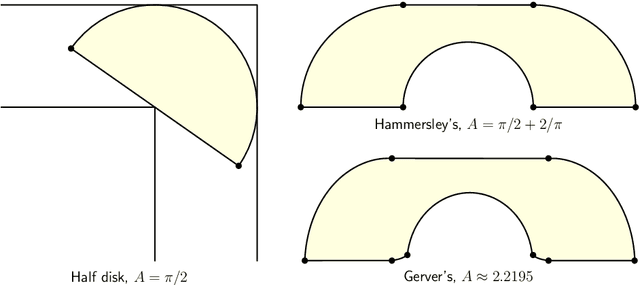
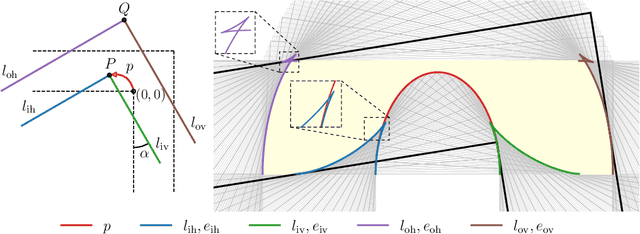
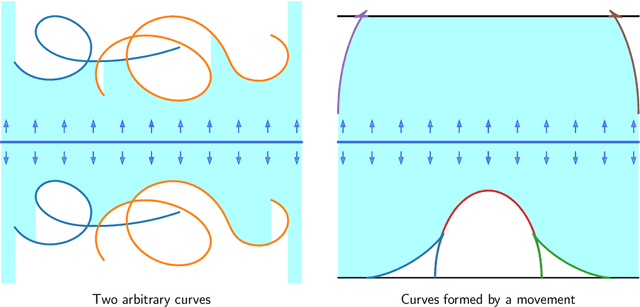
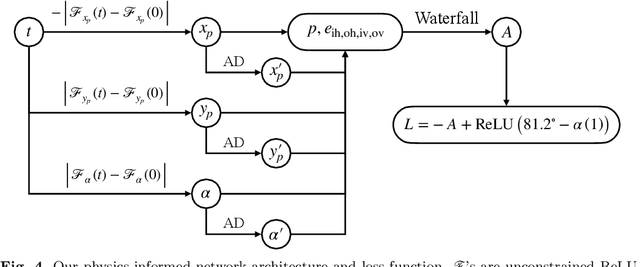
The Moving Sofa Problem, formally proposed by Leo Moser in 1966, seeks to determine the largest area of a two-dimensional shape that can navigate through an $L$-shaped corridor with unit width. The current best lower bound is about 2.2195, achieved by Joseph Gerver in 1992, though its global optimality remains unproven. In this paper, we investigate this problem by leveraging the universal approximation strength and computational efficiency of neural networks. We report two approaches, both supporting Gerver's conjecture that his shape is the unique global maximum. Our first approach is continuous function learning. We drop Gerver's assumptions that i) the rotation of the corridor is monotonic and symmetric and, ii) the trajectory of its corner as a function of rotation is continuously differentiable. We parameterize rotation and trajectory by independent piecewise linear neural networks (with input being some pseudo time), allowing for rich movements such as backward rotation and pure translation. We then compute the sofa area as a differentiable function of rotation and trajectory using our "waterfall" algorithm. Our final loss function includes differential terms and initial conditions, leveraging the principles of physics-informed machine learning. Under such settings, extensive training starting from diverse function initialization and hyperparameters is conducted, unexceptionally showing rapid convergence to Gerver's solution. Our second approach is via discrete optimization of the Kallus-Romik upper bound, which converges to the maximum sofa area from above as the number of rotation angles increases. We uplift this number to 10000 to reveal its asymptotic behavior. It turns out that the upper bound yielded by our models does converge to Gerver's area (within an error of 0.01% when the number of angles reaches 2100). We also improve their five-angle upper bound from 2.37 to 2.3337.

Zero Coordinate Shift: Whetted Automatic Differentiation for Physics-informed Operator Learning

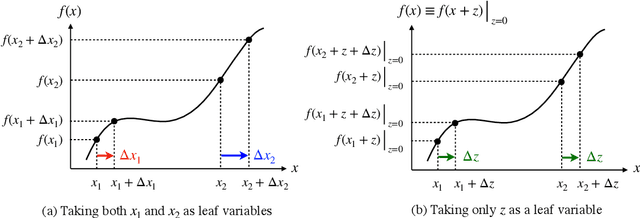
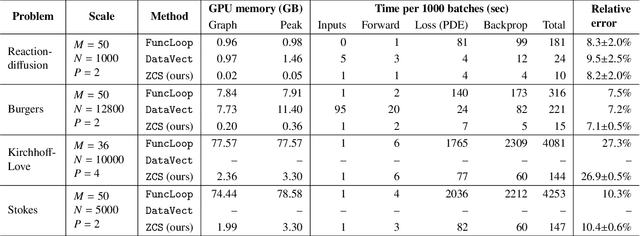
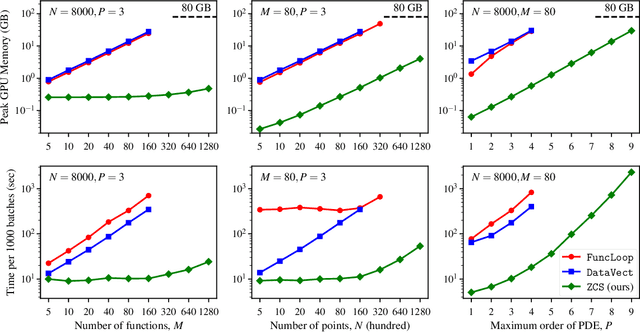
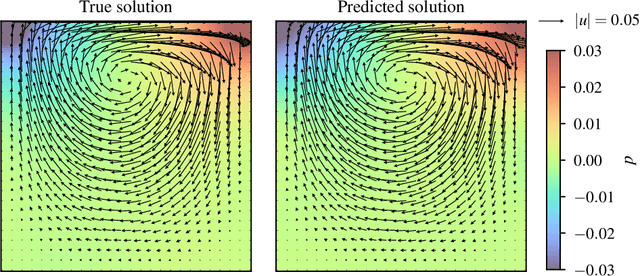
Automatic differentiation (AD) is a critical step in physics-informed machine learning, required for computing the high-order derivatives of network output w.r.t. coordinates. In this paper, we present a novel and lightweight algorithm to conduct such AD for physics-informed operator learning, as we call the trick of Zero Coordinate Shift (ZCS). Instead of making all sampled coordinates leaf variables, ZCS introduces only one scalar-valued leaf variable for each spatial or temporal dimension, leading to a game-changing performance leap by simplifying the wanted derivatives from "many-roots-many-leaves" to "one-root-many-leaves". ZCS is easy to implement with current deep learning libraries; our own implementation is by extending the DeepXDE package. We carry out a comprehensive benchmark analysis and several case studies, training physics-informed DeepONets to solve partial differential equations (PDEs) without data. The results show that ZCS has persistently brought down GPU memory consumption and wall time for training by an order of magnitude, with the savings increasing with problem scale (i.e., number of functions, number of points and order of PDE). As a low-level optimisation, ZCS entails no restrictions on data, physics (PDEs) or network architecture and does not compromise training results from any aspect.

Padding-free Convolution based on Preservation of Differential Characteristics of Kernels

Convolution is a fundamental operation in image processing and machine learning. Aimed primarily at maintaining image size, padding is a key ingredient of convolution, which, however, can introduce undesirable boundary effects. We present a non-padding-based method for size-keeping convolution based on the preservation of differential characteristics of kernels. The main idea is to make convolution over an incomplete sliding window "collapse" to a linear differential operator evaluated locally at its central pixel, which no longer requires information from the neighbouring missing pixels. While the underlying theory is rigorous, our final formula turns out to be simple: the convolution over an incomplete window is achieved by convolving its nearest complete window with a transformed kernel. This formula is computationally lightweight, involving neither interpolation or extrapolation nor restrictions on image and kernel sizes. Our method favours data with smooth boundaries, such as high-resolution images and fields from physics. Our experiments include: i) filtering analytical and non-analytical fields from computational physics and, ii) training convolutional neural networks (CNNs) for the tasks of image classification, semantic segmentation and super-resolution reconstruction. In all these experiments, our method has exhibited visible superiority over the compared ones.

On the Compatibility between a Neural Network and a Partial Differential Equation for Physics-informed Learning

We shed light on a pitfall and an opportunity in physics-informed neural networks (PINNs). We prove that a multilayer perceptron (MLP) only with ReLU (Rectified Linear Unit) or ReLU-like Lipschitz activation functions will always lead to a vanished Hessian. Such a network-imposed constraint contradicts any second- or higher-order partial differential equations (PDEs). Therefore, a ReLU-based MLP cannot form a permissible function space for the approximation of their solutions. Inspired by this pitfall, we prove that a linear PDE up to the $n$-th order can be strictly satisfied by an MLP with $C^n$ activation functions when the weights of its output layer lie on a certain hyperplane, as called the out-layer-hyperplane. An MLP equipped with the out-layer-hyperplane becomes "physics-enforced", no longer requiring a loss function for the PDE itself (but only those for the initial and boundary conditions). Such a hyperplane exists not only for MLPs but for any network architecture tailed by a fully-connected hidden layer. To our knowledge, this should be the first PINN architecture that enforces point-wise correctness of a PDE. We give the closed-form expression of the out-layer-hyperplane for second-order linear PDEs and provide an implementation.