WaveMax: Radar Waveform Design via Convex Maximization of FrFT Phase Retrieval

The ambiguity function (AF) is a critical tool in radar waveform design, representing the two-dimensional correlation between a transmitted signal and its time-delayed, frequency-shifted version. Obtaining a radar signal to match a specified AF magnitude is a bi-variate variant of the well-known phase retrieval problem. Prior approaches to this problem were either limited to a few classes of waveforms or lacked a computable procedure to estimate the signal. Our recent work provided a framework for solving this problem for both band- and time-limited signals using non-convex optimization. In this paper, we introduce a novel approach WaveMax that formulates waveform recovery as a convex optimization problem by relying on the fractional Fourier transform (FrFT)-based AF. We exploit the fact that AF of the FrFT of the original signal is equivalent to a rotation of the original AF. In particular, we reconstruct the radar signal by solving a low-rank minimization problem, which approximates the waveform using the leading eigenvector of a matrix derived from the AF. Our theoretical analysis shows that unique waveform reconstruction is achievable with a sample size no more than three times the signal frequencies or time samples. Numerical experiments validate the efficacy of WaveMax in recovering signals from noiseless and noisy AF, including scenarios with randomly and uniformly sampled sparse data.

Deep Learning Evidence for Global Optimality of Gerver's Sofa

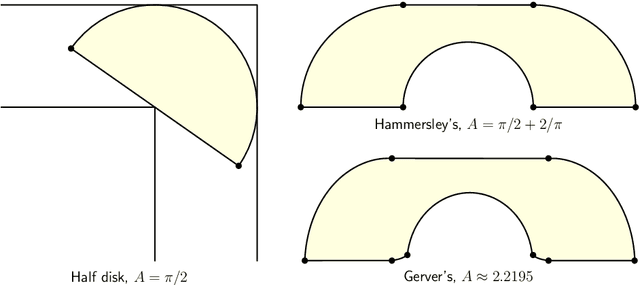
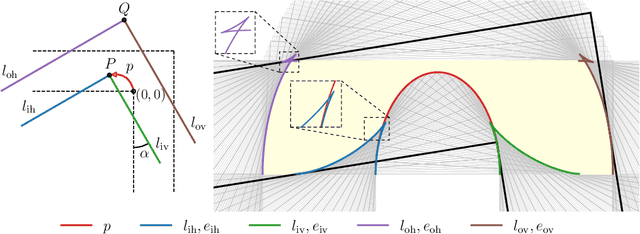
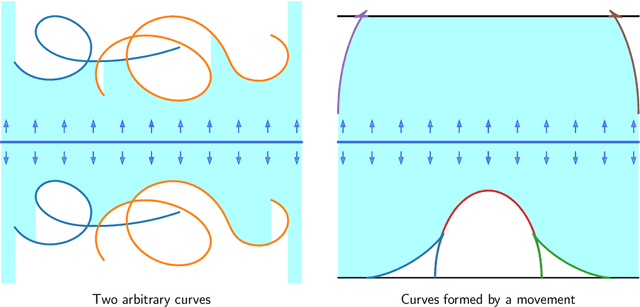
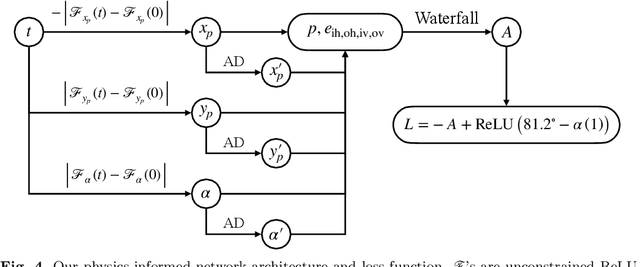
The Moving Sofa Problem, formally proposed by Leo Moser in 1966, seeks to determine the largest area of a two-dimensional shape that can navigate through an $L$-shaped corridor with unit width. The current best lower bound is about 2.2195, achieved by Joseph Gerver in 1992, though its global optimality remains unproven. In this paper, we investigate this problem by leveraging the universal approximation strength and computational efficiency of neural networks. We report two approaches, both supporting Gerver's conjecture that his shape is the unique global maximum. Our first approach is continuous function learning. We drop Gerver's assumptions that i) the rotation of the corridor is monotonic and symmetric and, ii) the trajectory of its corner as a function of rotation is continuously differentiable. We parameterize rotation and trajectory by independent piecewise linear neural networks (with input being some pseudo time), allowing for rich movements such as backward rotation and pure translation. We then compute the sofa area as a differentiable function of rotation and trajectory using our "waterfall" algorithm. Our final loss function includes differential terms and initial conditions, leveraging the principles of physics-informed machine learning. Under such settings, extensive training starting from diverse function initialization and hyperparameters is conducted, unexceptionally showing rapid convergence to Gerver's solution. Our second approach is via discrete optimization of the Kallus-Romik upper bound, which converges to the maximum sofa area from above as the number of rotation angles increases. We uplift this number to 10000 to reveal its asymptotic behavior. It turns out that the upper bound yielded by our models does converge to Gerver's area (within an error of 0.01% when the number of angles reaches 2100). We also improve their five-angle upper bound from 2.37 to 2.3337.

Group-Theoretic Wideband Radar Waveform Design

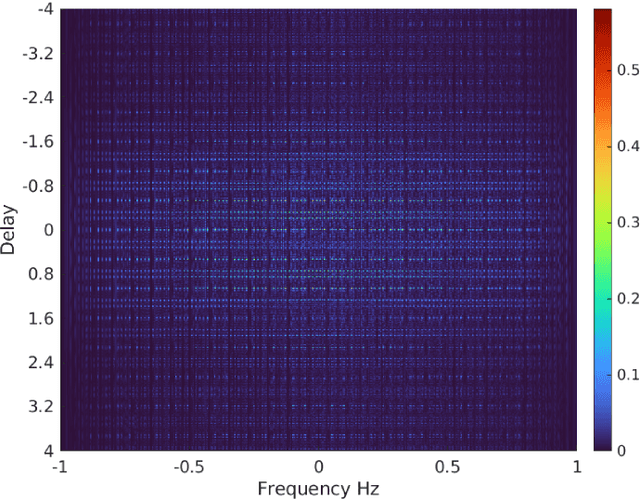
We investigate the theory of affine groups in the context of designing radar waveforms that obey the desired wideband ambiguity function (WAF). The WAF is obtained by correlating the signal with its time-dilated, Doppler-shifted, and delayed replicas. We consider the WAF definition as a coefficient function of the unitary representation of the group $a\cdot x + b$. This is essentially an algebraic problem applied to the radar waveform design. Prior works on this subject largely analyzed narrow-band ambiguity functions. Here, we show that when the underlying wideband signal of interest is a pulse or pulse train, a tight frame can be built to design that waveform. Specifically, we design the radar signals by minimizing the ratio of bounding constants of the frame in order to obtain lower sidelobes in the WAF. This minimization is performed by building a codebook based on difference sets in order to achieve the Welch bound. We show that the tight frame so obtained is connected with the wavelet transform that defines the WAF.

An Overview of Advances in Signal Processing Techniques for Classical and Quantum Wideband Synthetic Apertures

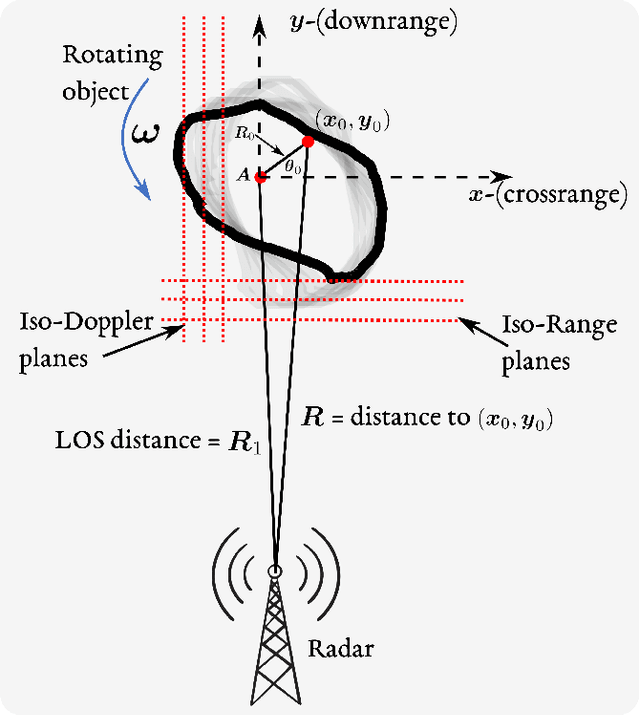
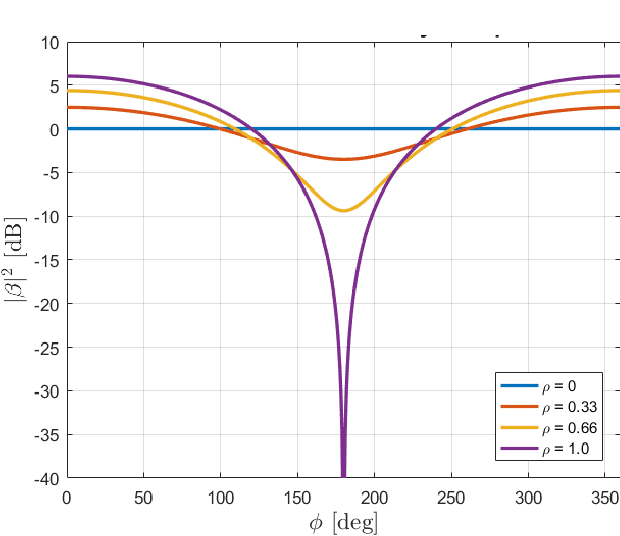
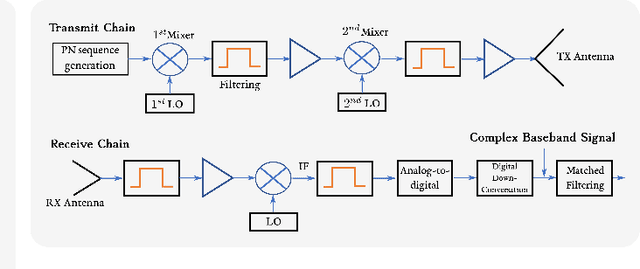
Rapid developments in synthetic aperture (SA) systems, which generate a larger aperture with greater angular resolution than is inherently possible from the physical dimensions of a single sensor alone, are leading to novel research avenues in several signal processing applications. The SAs may either use a mechanical positioner to move an antenna through space or deploy a distributed network of sensors. With the advent of new hardware technologies, the SAs tend to be denser nowadays. The recent opening of higher frequency bands has led to wide SA bandwidths. In general, new techniques and setups are required to harness the potential of wide SAs in space and bandwidth. Herein, we provide a brief overview of emerging signal processing trends in such spatially and spectrally wideband SA systems. This guide is intended to aid newcomers in navigating the most critical issues in SA analysis and further supports the development of new theories in the field. In particular, we cover the theoretical framework and practical underpinnings of wideband SA radar, channel sounding, sonar, radiometry, and optical applications. Apart from the classical SA applications, we also discuss the quantum electric-field-sensing probes in SAs that are currently undergoing active research but remain at nascent stages of development.

Hybrid Diffractive Optics Design via Hardware-in-the-Loop Methodology for Achromatic Extended-Depth-of-Field Imaging

End-to-end optimization of diffractive optical elements (DOEs) profile through a digital differentiable model combined with computational imaging have gained an increasing attention in emerging applications due to the compactness of resultant physical setups. Despite recent works have shown the potential of this methodology to design optics, its performance in physical setups is still limited and affected by manufacturing artifacts of DOE, mismatch between simulated and resultant experimental point spread functions, and calibration errors. Additionally, the computational burden of the digital differentiable model to effectively design the DOE is increasing, thus limiting the size of the DOE that can be designed. To overcome the above mentioned limitations, the broadband imaging system with phase-only spatial light modulator (SLM) as an encoded DOE is proposed and developed in this paper. A co-design of the SLM phase pattern and image reconstruction algorithm is produced following the end-to-end strategy, using for optimization a convolutional neural network equipped with quantitative and qualitative loss functions. The optics of the imaging system is hybrid consisting of SLM as DOE and refractive lens. SLM phase-pattern is optimized by applying the Hardware-in-the-loop technique, which helps to eliminate the mismatch between numerical modeling and physical reality of image formation as light propagation is not numerically modeled but is physically done. In our experiments, the hybrid optics is implemented by the optical projection of the SLM phase-pattern on a lens plane for a depth range 0.4-1.9m. Comparison with compound multi-lens optics such as Sony A7 III and iPhone Xs Max cameras show that the proposed system is advanced in all-in-focus sharp imaging.

Unfolding-Aided Bootstrapped Phase Retrieval in Optical Imaging

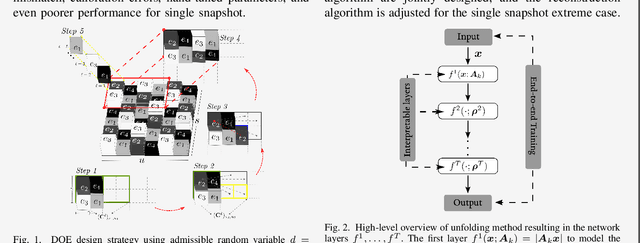
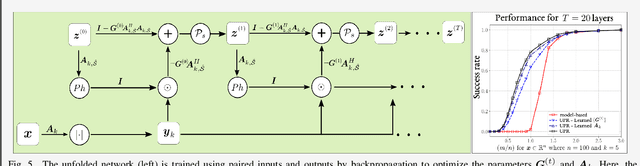
Phase retrieval in optical imaging refers to the recovery of a complex signal from phaseless data acquired in the form of its diffraction patterns. These patterns are acquired through a system with a coherent light source that employs a diffractive optical element (DOE) to modulate the scene resulting in coded diffraction patterns at the sensor. Recently, the hybrid approach of model-driven network or deep unfolding has emerged as an effective alternative because it allows for bounding the complexity of phase retrieval algorithms while also retaining their efficacy. Additionally, such hybrid approaches have shown promise in improving the design of DOEs that follow theoretical uniqueness conditions. There are opportunities to exploit novel experimental setups and resolve even more complex DOE phase retrieval applications. This paper presents an overview of algorithms and applications of deep unfolding for bootstrapped - regardless of near, middle, and far zones - phase retrieval.

Phase Retrieval for Radar Waveform Design

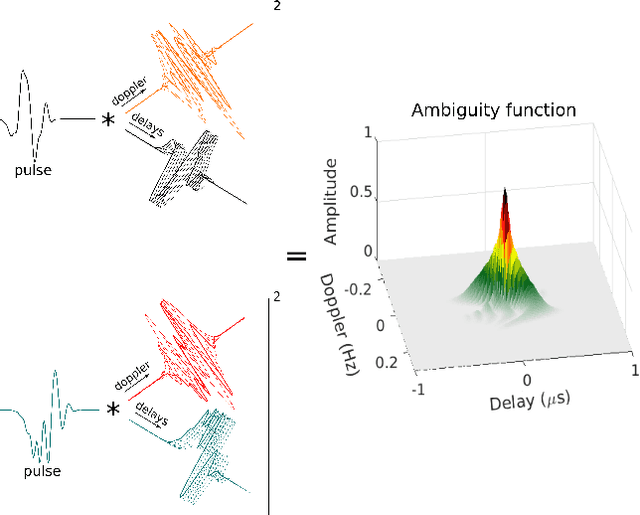
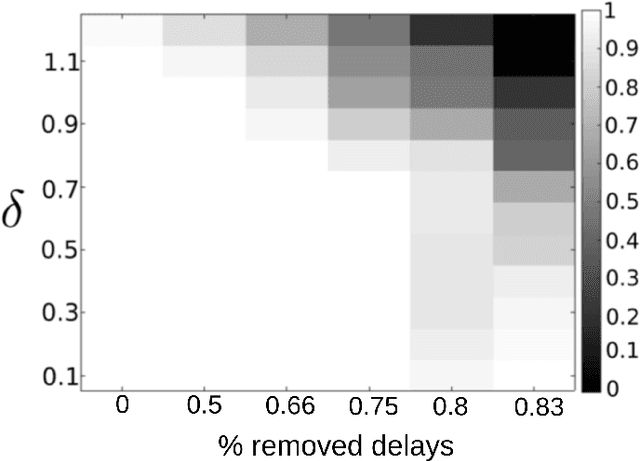
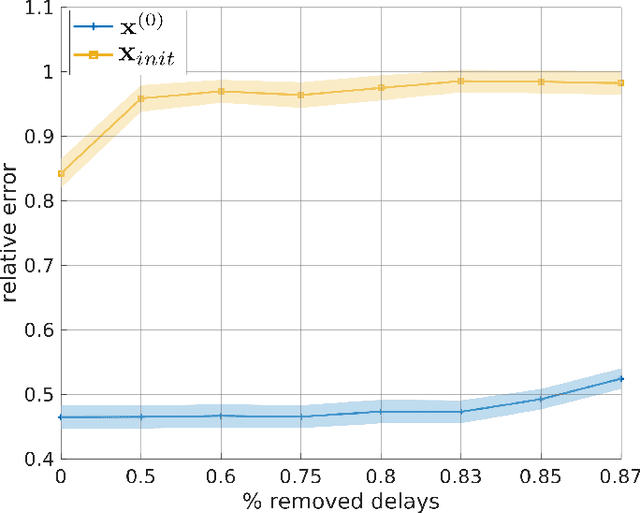
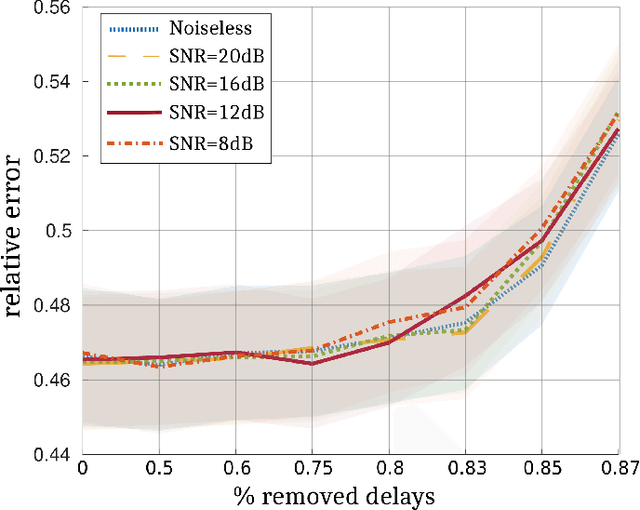
The ability of a radar to discriminate in both range and Doppler velocity is completely characterized by the ambiguity function (AF) of its transmit waveform. Mathematically, it is obtained by correlating the waveform with its Doppler-shifted and delayed replicas. We consider the inverse problem of designing a radar transmit waveform that satisfies the specified AF magnitude. This process can be viewed as a signal reconstruction with some variation of phase retrieval methods. We provide a trust-region algorithm that minimizes a smoothed non-convex least-squares objective function to iteratively recover the underlying signal-of-interest for either time- or band-limited support. The method first approximates the signal using an iterative spectral algorithm and then refines the attained initialization based upon a sequence of gradient iterations. Our theoretical analysis shows that unique signal reconstruction is possible using signal samples no more than thrice the number of signal frequencies or time samples. Numerical experiments demonstrate that our method recovers both time- and band-limited signals from even sparsely and randomly sampled AFs with mean-square-error of $1\times 10^{-6}$ and $9\times 10^{-2}$ for the full noiseless samples and sparse noisy samples, respectively.

Non-Convex Recovery from Phaseless Low-Resolution Blind Deconvolution Measurements using Noisy Masked Patterns

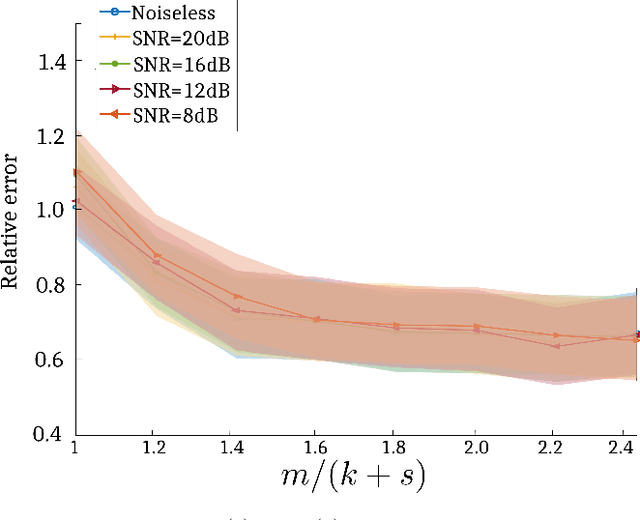
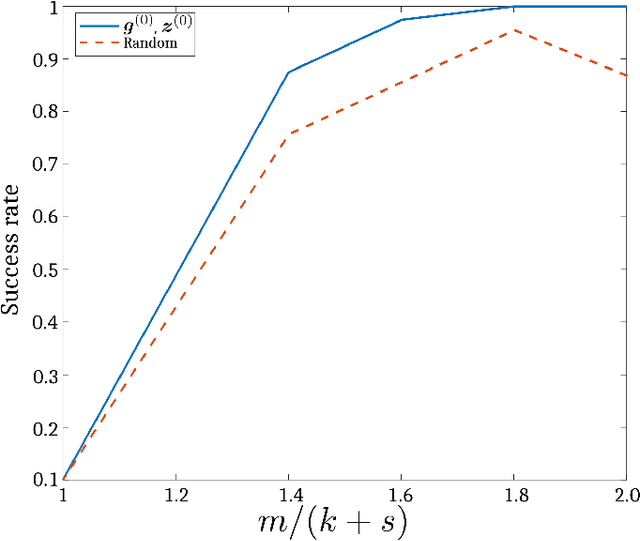
This paper addresses recovery of a kernel $\boldsymbol{h}\in \mathbb{C}^{n}$ and a signal $\boldsymbol{x}\in \mathbb{C}^{n}$ from the low-resolution phaseless measurements of their noisy circular convolution $\boldsymbol{y} = \left \rvert \boldsymbol{F}_{lo}( \boldsymbol{x}\circledast \boldsymbol{h}) \right \rvert^{2} + \boldsymbol{\eta}$, where $\boldsymbol{F}_{lo}\in \mathbb{C}^{m\times n}$ stands for a partial discrete Fourier transform ($m<n$), $\boldsymbol{\eta}$ models the noise, and $\lvert \cdot \rvert$ is the element-wise absolute value function. This problem is severely ill-posed because both the kernel and signal are unknown and, in addition, the measurements are phaseless, leading to many $\boldsymbol{x}$-$\boldsymbol{h}$ pairs that correspond to the measurements. Therefore, to guarantee a stable recovery of $\boldsymbol{x}$ and $\boldsymbol{h}$ from $\boldsymbol{y}$, we assume that the kernel $\boldsymbol{h}$ and the signal $\boldsymbol{x}$ lie in known subspaces of dimensions $k$ and $s$, respectively, such that $m\gg k+s$. We solve this problem by proposing a blind deconvolution algorithm for phaseless super-resolution (BliPhaSu) to minimize a non-convex least-squares objective function. The method first estimates a low-resolution version of both signals through a spectral algorithm, which are then refined based upon a sequence of stochastic gradient iterations. We show that our BliPhaSu algorithm converges linearly to a pair of true signals on expectation under a proper initialization that is based on spectral method. Numerical results from experimental data demonstrate perfect recovery of both $\boldsymbol{h}$ and $\boldsymbol{x}$ using our method.

Unique Bispectrum Inversion for Signals with Finite Spectral/Temporal Support

Retrieving a signal from the Fourier transform of its third-order statistics or bispectrum arises in a wide range of signal processing problems. Conventional methods do not provide a unique inversion of bispectrum. In this paper, we present a an approach that uniquely recovers signals with finite spectral support (band-limited signals) from at least $3B$ measurements of its bispectrum function (BF), where $B$ is the signal's bandwidth. Our approach also extends to time-limited signals. We propose a two-step trust region algorithm that minimizes a non-convex objective function. First, we approximate the signal by a spectral algorithm. Then, we refine the attained initialization based upon a sequence of gradient iterations. Numerical experiments suggest that our proposed algorithm is able to estimate band/time-limited signals from its BF for both complete and undersampled observations.

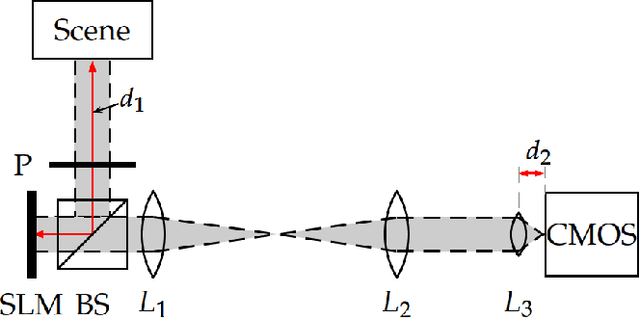
Optimized Power-Balanced Hybrid Phase-Coded Optics and Inverse Imaging for Achromatic EDoF

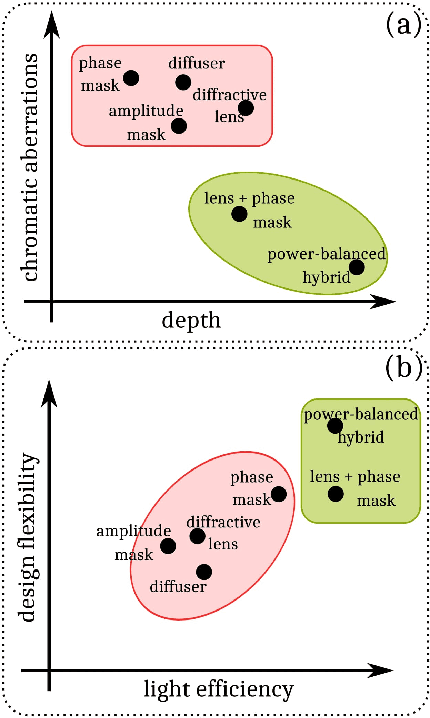
The power-balanced hybrid optical imaging system is a special design of a computational camera, introduced in this paper, with image formation by a refractive lens and Multilevel Phase Mask (MPM) as a diffractive optical element (DoE). This system provides a long focal depth and low chromatic aberrations thanks to MPM, and a high energy light concentration due to the refractive lens. This paper additionally introduces the concept of a optimal power balance between lens and MPM for achromatic extended-depth-of-field (EDoF) imaging. To optimize this power-balance as well as to optimize MPM using Neural Network techniques, we build a fully-differentiable image formation model for joint optimization of optical and imaging parameters for the designed computational camera. Additionally, we determine a Wiener-like inverse imaging optimal optical transfer function (OTF) to reconstruct a sharp image from the defocused observation. We numerically and experimentally compare the designed system with its counterparts, lensless and just-lens optical systems, for the visible wavelength interval (400-700) nm and the EDoF range (0.5-1000) m. The attained results demonstrate that the proposed system equipped with the optimal OTF overcomes its lensless and just-lens counterparts (even when they are used with optimized OTFs) in terms of reconstruction quality for off-focus distances.