Linearization Explains Fine-Tuning in Large Language Models

Parameter-Efficient Fine-Tuning (PEFT) is a popular class of techniques that strive to adapt large models in a scalable and resource-efficient manner. Yet, the mechanisms underlying their training performance and generalization remain underexplored. In this paper, we provide several insights into such fine-tuning through the lens of linearization. Fine-tuned models are often implicitly encouraged to remain close to the pretrained model. By making this explicit, using an Euclidean distance inductive bias in parameter space, we show that fine-tuning dynamics become equivalent to learning with the positive-definite neural tangent kernel (NTK). We specifically analyze how close the fully linear and the linearized fine-tuning optimizations are, based on the strength of the regularization. This allows us to be pragmatic about how good a model linearization is when fine-tuning large language models (LLMs). When linearization is a good model, our findings reveal a strong correlation between the eigenvalue spectrum of the NTK and the performance of model adaptation. Motivated by this, we give spectral perturbation bounds on the NTK induced by the choice of layers selected for fine-tuning. We empirically validate our theory on Low Rank Adaptation (LoRA) on LLMs. These insights not only characterize fine-tuning but also have the potential to enhance PEFT techniques, paving the way to better informed and more nimble adaptation in LLMs.

Fast and Robust LRSD-based SAR/ISAR Imaging and Decomposition

The earlier works in the context of low-rank-sparse-decomposition (LRSD)-driven stationary synthetic aperture radar (SAR) imaging have shown significant improvement in the reconstruction-decomposition process. Neither of the proposed frameworks, however, can achieve satisfactory performance when facing a platform residual phase error (PRPE) arising from the instability of airborne platforms. More importantly, in spite of the significance of real-time processing requirements in remote sensing applications, these prior works have only focused on enhancing the quality of the formed image, not reducing the computational burden. To address these two concerns, this article presents a fast and unified joint SAR imaging framework where the dominant sparse objects and low-rank features of the image background are decomposed and enhanced through a robust LRSD. In particular, our unified algorithm circumvents the tedious task of computing the inverse of large matrices for image formation and takes advantage of the recent advances in constrained quadratic programming to handle the unimodular constraint imposed due to the PRPE. Furthermore, we extend our approach to ISAR autofocusing and imaging. Specifically, due to the intrinsic sparsity of ISAR images, the LRSD framework is essentially tasked with the recovery of a sparse image. Several experiments based on synthetic and real data are presented to validate the superiority of the proposed method in terms of imaging quality and computational cost compared to the state-of-the-art methods.

Predicting Through Generation: Why Generation Is Better for Prediction

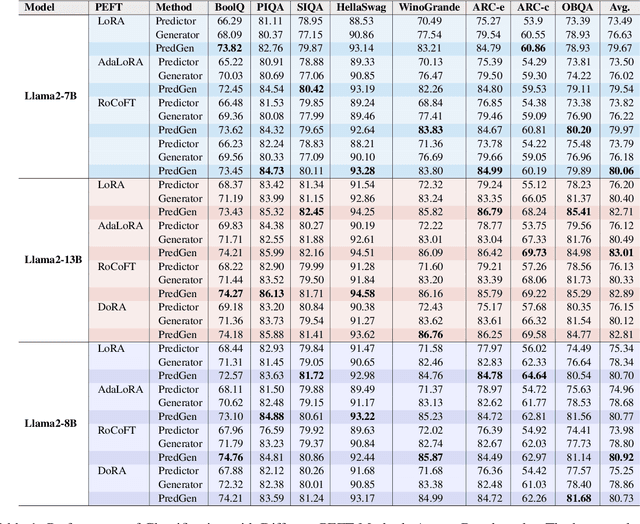
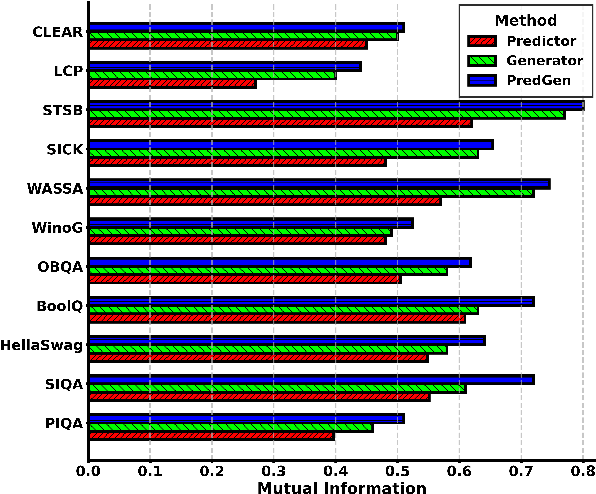
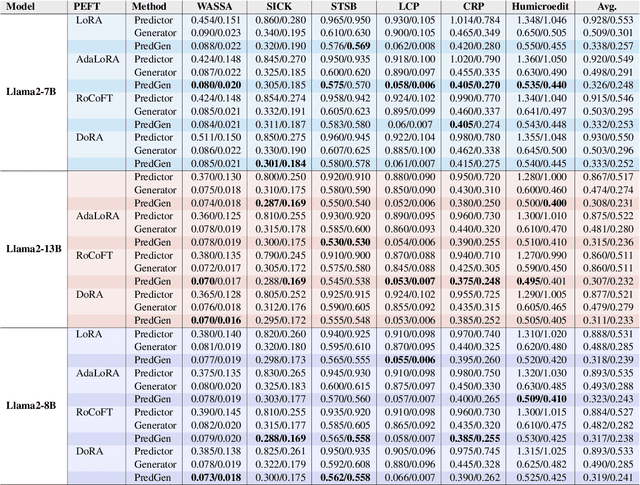
This paper argues that generating output tokens is more effective than using pooled representations for prediction tasks because token-level generation retains more mutual information. Since LLMs are trained on massive text corpora using next-token prediction, generation aligns naturally with their learned behavior. Using the Data Processing Inequality (DPI), we provide both theoretical and empirical evidence supporting this claim. However, autoregressive models face two key challenges when used for prediction: (1) exposure bias, where the model sees ground truth tokens during training but relies on its own predictions during inference, leading to errors, and (2) format mismatch, where discrete tokens do not always align with the tasks required output structure. To address these challenges, we introduce PredGen(Predicting Through Generating), an end to end framework that (i) uses scheduled sampling to reduce exposure bias, and (ii) introduces a task adapter to convert the generated tokens into structured outputs. Additionally, we introduce Writer-Director Alignment Loss (WDAL), which ensures consistency between token generation and final task predictions, improving both text coherence and numerical accuracy. We evaluate PredGen on multiple classification and regression benchmarks. Our results show that PredGen consistently outperforms standard baselines, demonstrating its effectiveness in structured prediction tasks.

Unlocking Efficient Large Inference Models: One-Bit Unrolling Tips the Scales

Recent advancements in Large Language Model (LLM) compression, such as BitNet and BitNet b1.58, have marked significant strides in reducing the computational demands of LLMs through innovative one-bit quantization techniques. We extend this frontier by looking at Large Inference Models (LIMs) that have become indispensable across various applications. However, their scale and complexity often come at a significant computational cost. We introduce a novel approach that leverages one-bit algorithm unrolling, effectively integrating information from the physical world in the model architecture. Our method achieves a bit-per-link rate significantly lower than the 1.58 bits reported in prior work, thanks to the natural sparsity that emerges in our network architectures. We numerically demonstrate that the proposed one-bit algorithm unrolling scheme can improve both training and test outcomes by effortlessly increasing the number of layers while substantially compressing the network. Additionally, we provide theoretical results on the generalization gap, convergence rate, stability, and sensitivity of our proposed one-bit algorithm unrolling.

RoCoFT: Efficient Finetuning of Large Language Models with Row-Column Updates

We propose RoCoFT, a parameter-efficient fine-tuning method for large-scale language models (LMs) based on updating only a few rows and columns of the weight matrices in transformers. Through extensive experiments with medium-size LMs like BERT and RoBERTa, and larger LMs like Bloom-7B, Llama2-7B, and Llama2-13B, we show that our method gives comparable or better accuracies than state-of-art PEFT methods while also being more memory and computation-efficient. We also study the reason behind the effectiveness of our method with tools from neural tangent kernel theory. We empirically demonstrate that our kernel, constructed using a restricted set of row and column parameters, are numerically close to the full-parameter kernel and gives comparable classification performance. Ablation studies are conducted to investigate the impact of different algorithmic choices, including the selection strategy for rows and columns as well as the optimal rank for effective implementation of our method.

Data-Aware Training Quality Monitoring and Certification for Reliable Deep Learning

Deep learning models excel at capturing complex representations through sequential layers of linear and non-linear transformations, yet their inherent black-box nature and multi-modal training landscape raise critical concerns about reliability, robustness, and safety, particularly in high-stakes applications. To address these challenges, we introduce YES training bounds, a novel framework for real-time, data-aware certification and monitoring of neural network training. The YES bounds evaluate the efficiency of data utilization and optimization dynamics, providing an effective tool for assessing progress and detecting suboptimal behavior during training. Our experiments show that the YES bounds offer insights beyond conventional local optimization perspectives, such as identifying when training losses plateau in suboptimal regions. Validated on both synthetic and real data, including image denoising tasks, the bounds prove effective in certifying training quality and guiding adjustments to enhance model performance. By integrating these bounds into a color-coded cloud-based monitoring system, we offer a powerful tool for real-time evaluation, setting a new standard for training quality assurance in deep learning.

Deep Learning-Enabled One-Bit DoA Estimation

Unrolled deep neural networks have attracted significant attention for their success in various practical applications. In this paper, we explore an application of deep unrolling in the direction of arrival (DoA) estimation problem when coarse quantization is applied to the measurements. We present a compressed sensing formulation for DoA estimation from one-bit data in which estimating target DoAs requires recovering a sparse signal from a limited number of severely quantized linear measurements. In particular, we exploit covariance recovery from one-bit dither samples. To recover the covariance of transmitted signal, the learned iterative shrinkage and thresholding algorithm (LISTA) is employed fed by one-bit data. We demonstrate that the upper bound of estimation performance is governed by the recovery error of the transmitted signal covariance matrix. Through numerical experiments, we demonstrate the proposed LISTA-based algorithm's capability in estimating target locations. The code employed in this study is available online.

Antenna Failure Resilience: Deep Learning-Enabled Robust DOA Estimation with Single Snapshot Sparse Arrays

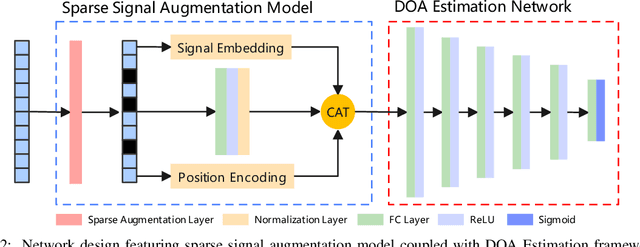
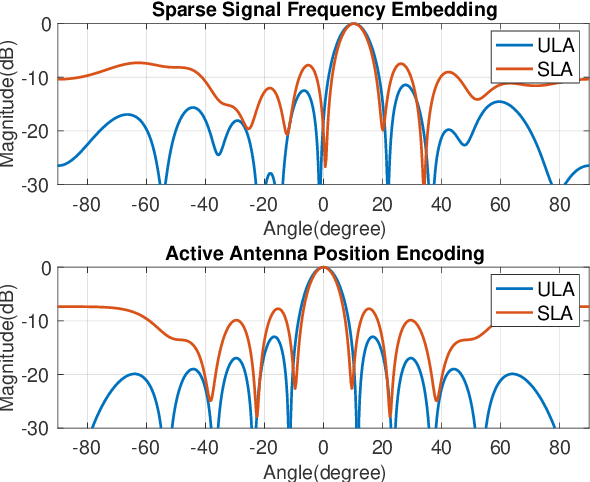
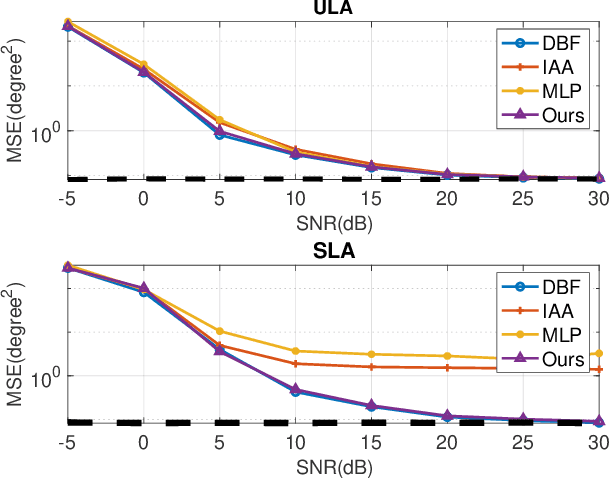
Recent advancements in Deep Learning (DL) for Direction of Arrival (DOA) estimation have highlighted its superiority over traditional methods, offering faster inference, enhanced super-resolution, and robust performance in low Signal-to-Noise Ratio (SNR) environments. Despite these advancements, existing research predominantly focuses on multi-snapshot scenarios, a limitation in the context of automotive radar systems which demand high angular resolution and often rely on limited snapshots, sometimes as scarce as a single snapshot. Furthermore, the increasing interest in sparse arrays for automotive radar, owing to their cost-effectiveness and reduced antenna element coupling, presents additional challenges including susceptibility to random sensor failures. This paper introduces a pioneering DL framework featuring a sparse signal augmentation layer, meticulously crafted to bolster single snapshot DOA estimation across diverse sparse array setups and amidst antenna failures. To our best knowledge, this is the first work to tackle this issue. Our approach improves the adaptability of deep learning techniques to overcome the unique difficulties posed by sparse arrays with single snapshot. We conduct thorough evaluations of our network's performance using simulated and real-world data, showcasing the efficacy and real-world viability of our proposed solution. The code and real-world dataset employed in this study are available at https://github.com/ruxinzh/Deep_RSA_DOA.

Collaborative Automotive Radar Sensing via Mixed-Precision Distributed Array Completion

This paper investigates the effects of coarse quantization with mixed precision on measurements obtained from sparse linear arrays, synthesized by a collaborative automotive radar sensing strategy. The mixed quantization precision significantly reduces the data amount that needs to be shared from radar nodes to the fusion center for coherent processing. We utilize the low-rank properties inherent in the constructed Hankel matrix of the mixed-precision array, to recover azimuth angles from quantized measurements. Our proposed approach addresses the challenge of mixed-quantized Hankel matrix completion, allowing for accurate estimation of the azimuth angles of interest. To evaluate the recovery performance of the proposed scheme, we establish a quasi-isometric embedding with a high probability for mixed-precision quantization. The effectiveness of our proposed scheme is demonstrated through numerical results, highlighting successful reconstruction.

Beyond Diagonal RIS: Key to Next-Generation Integrated Sensing and Communications?

Reconfigurable intelligent surface (RIS) have introduced unprecedented flexibility and adaptability toward smart wireless channels. Recent research on integrated sensing and communication (ISAC) systems has demonstrated that RIS platforms enable enhanced signal quality, coverage, and link capacity. In this paper, we explore the application of fully-connected beyond diagonal RIS (BD-RIS) to ISAC systems. BD-RIS introduces additional degrees of freedom by allowing non-zero off-diagonal elements for the scattering matrix, potentially enabling further functionalities and performance enhancements. In particular, we consider the joint design objective of maximizing the weighted sum of the signal-to-noise ratio (SNR) at the radar receiver and communication users by leveraging the extra degrees-of-freedom offered in the BD-RIS setting. These degrees-of-freedom are unleashed by formulating an alternating optimization process over known and auxiliary (latent) variables of such systems. Our numerical results reveal the advantages of deploying BD-RIS in the context of ISAC and the effectiveness of the proposed algorithm by improving the SNR values for both radar and communication users by several orders of magnitude.