Data-Aware Training Quality Monitoring and Certification for Reliable Deep Learning

Deep learning models excel at capturing complex representations through sequential layers of linear and non-linear transformations, yet their inherent black-box nature and multi-modal training landscape raise critical concerns about reliability, robustness, and safety, particularly in high-stakes applications. To address these challenges, we introduce YES training bounds, a novel framework for real-time, data-aware certification and monitoring of neural network training. The YES bounds evaluate the efficiency of data utilization and optimization dynamics, providing an effective tool for assessing progress and detecting suboptimal behavior during training. Our experiments show that the YES bounds offer insights beyond conventional local optimization perspectives, such as identifying when training losses plateau in suboptimal regions. Validated on both synthetic and real data, including image denoising tasks, the bounds prove effective in certifying training quality and guiding adjustments to enhance model performance. By integrating these bounds into a color-coded cloud-based monitoring system, we offer a powerful tool for real-time evaluation, setting a new standard for training quality assurance in deep learning.

Deep Learning-Enabled One-Bit DoA Estimation

Unrolled deep neural networks have attracted significant attention for their success in various practical applications. In this paper, we explore an application of deep unrolling in the direction of arrival (DoA) estimation problem when coarse quantization is applied to the measurements. We present a compressed sensing formulation for DoA estimation from one-bit data in which estimating target DoAs requires recovering a sparse signal from a limited number of severely quantized linear measurements. In particular, we exploit covariance recovery from one-bit dither samples. To recover the covariance of transmitted signal, the learned iterative shrinkage and thresholding algorithm (LISTA) is employed fed by one-bit data. We demonstrate that the upper bound of estimation performance is governed by the recovery error of the transmitted signal covariance matrix. Through numerical experiments, we demonstrate the proposed LISTA-based algorithm's capability in estimating target locations. The code employed in this study is available online.

Collaborative Automotive Radar Sensing via Mixed-Precision Distributed Array Completion

This paper investigates the effects of coarse quantization with mixed precision on measurements obtained from sparse linear arrays, synthesized by a collaborative automotive radar sensing strategy. The mixed quantization precision significantly reduces the data amount that needs to be shared from radar nodes to the fusion center for coherent processing. We utilize the low-rank properties inherent in the constructed Hankel matrix of the mixed-precision array, to recover azimuth angles from quantized measurements. Our proposed approach addresses the challenge of mixed-quantized Hankel matrix completion, allowing for accurate estimation of the azimuth angles of interest. To evaluate the recovery performance of the proposed scheme, we establish a quasi-isometric embedding with a high probability for mixed-precision quantization. The effectiveness of our proposed scheme is demonstrated through numerical results, highlighting successful reconstruction.

Automotive Radar Sensing with Sparse Linear Arrays Using One-Bit Hankel Matrix Completion

The design of sparse linear arrays has proven instrumental in the implementation of cost-effective and efficient automotive radar systems for high-resolution imaging. This paper investigates the impact of coarse quantization on measurements obtained from such arrays. To recover azimuth angles from quantized measurements, we leverage the low-rank properties of the constructed Hankel matrix. In particular, by addressing the one-bit Hankel matrix completion problem through a developed singular value thresholding algorithm, our proposed approach accurately estimates the azimuth angles of interest. We provide comprehensive insights into recovery performance and the required number of one-bit samples. The effectiveness of our proposed scheme is underscored by numerical results, demonstrating successful reconstruction using only one-bit data.

Submodular Optimization for Placement of Intelligent Reflecting Surfaces in Sensing Systems

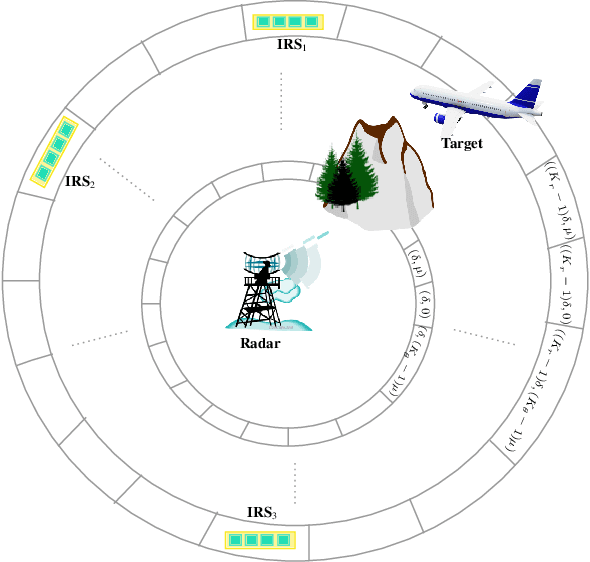
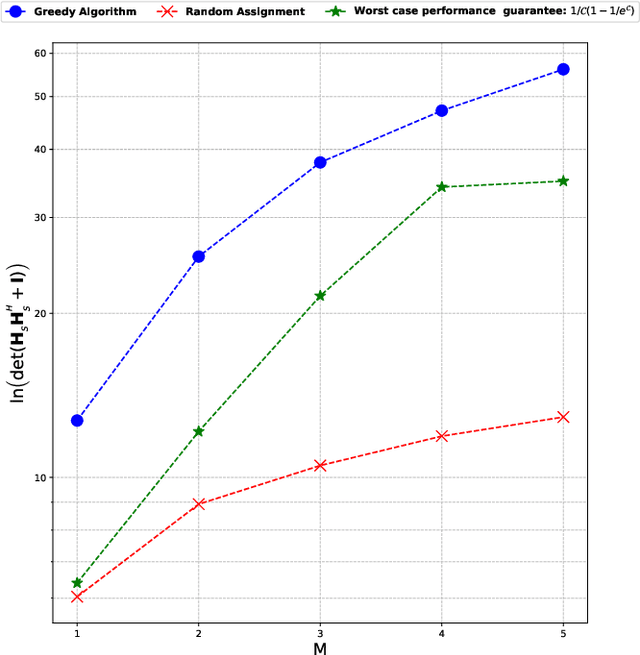
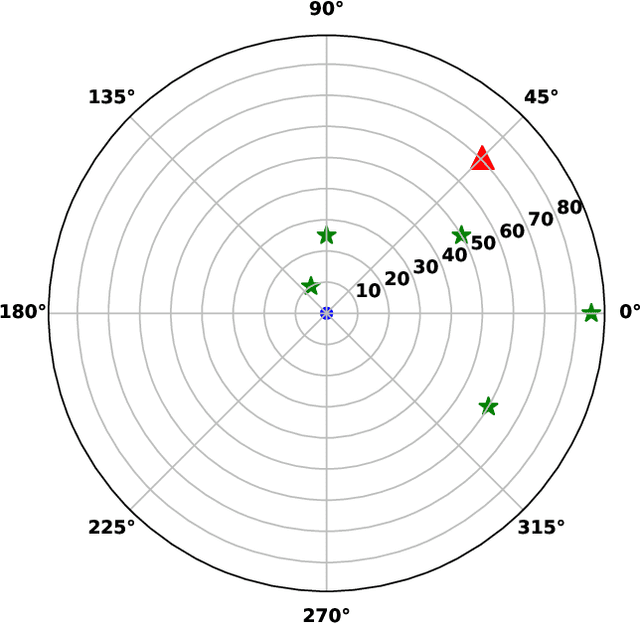
Intelligent reflecting surfaces (IRS) and their optimal deployment are the new technological frontier in sensing applications. Recently, IRS have demonstrated potential in advancing target estimation and detection. While the optimal phase-shift of IRS for different tasks has been studied extensively in the literature, the optimal placement of multiple IRS platforms for sensing applications is less explored. In this paper, we design the placement of IRS platforms for sensing by maximizing the mutual information. In particular, we use this criterion to determine an approximately optimal placement of IRS platforms to illuminate an area where the target has a hypothetical presence. After demonstrating the submodularity of the mutual information criteria, we tackle the design problem by means of a constant-factor approximation algorithm for submodular optimization. Numerical results are presented to validate the proposed submodular optimization framework for optimal IRS placement with worst case performance bounded to $1-1/e\approx 63 \%$.

Matrix Completion from One-Bit Dither Samples

We explore the impact of coarse quantization on matrix completion in the extreme scenario of dithered one-bit sensing, where the matrix entries are compared with time-varying threshold levels. In particular, instead of observing a subset of high-resolution entries of a low-rank matrix, we have access to a small number of one-bit samples, generated as a result of these comparisons. In order to recover the low-rank matrix using its coarsely quantized known entries, we begin by transforming the problem of one-bit matrix completion (one-bit MC) with time-varying thresholds into a nuclear norm minimization problem. The one-bit sampled information is represented as linear inequality feasibility constraints. We then develop the popular singular value thresholding (SVT) algorithm to accommodate these inequality constraints, resulting in the creation of the One-Bit SVT (OB-SVT). Our findings demonstrate that incorporating multiple time-varying sampling threshold sequences in one-bit MC can significantly improve the performance of the matrix completion algorithm. In pursuit of achieving this objective, we utilize diverse thresholding schemes, namely uniform, Gaussian, and discrete thresholds. To accelerate the convergence of our proposed algorithm, we introduce three variants of the OB-SVT algorithm. Among these variants is the randomized sketched OB-SVT, which departs from using the entire information at each iteration, opting instead to utilize sketched data. This approach effectively reduces the dimension of the operational space and accelerates the convergence. We perform numerical evaluations comparing our proposed algorithm with the maximum likelihood estimation method previously employed for one-bit MC, and demonstrate that our approach can achieve a better recovery performance.

HDR Imaging With One-Bit Quantization

Modulo sampling and dithered one-bit quantization frameworks have emerged as promising solutions to overcome the limitations of traditional analog-to-digital converters (ADCs) and sensors. Modulo sampling, with its high-resolution approach utilizing modulo ADCs, offers an unlimited dynamic range, while dithered one-bit quantization offers cost-efficiency and reduced power consumption while operating at elevated sampling rates. Our goal is to explore the synergies between these two techniques, leveraging their unique advantages, and to apply them to non-bandlimited signals within spline spaces. One noteworthy application of these signals lies in High Dynamic Range (HDR) imaging. In this paper, we expand upon the Unlimited One-Bit (UNO) sampling framework, initially conceived for bandlimited signals, to encompass non-bandlimited signals found in the context of HDR imaging. We present a novel algorithm rigorously examined for its ability to recover images from one-bit modulo samples. Additionally, we introduce a sufficient condition specifically designed for UNO sampling to perfectly recover non-bandlimited signals within spline spaces. Our numerical results vividly demonstrate the effectiveness of UNO sampling in the realm of HDR imaging.

One-Bit Quadratic Compressed Sensing: From Sample Abundance to Linear Feasibility

One-bit quantization with time-varying sampling thresholds has recently found significant utilization potential in statistical signal processing applications due to its relatively low power consumption and low implementation cost. In addition to such advantages, an attractive feature of one-bit analog-to-digital converters (ADCs) is their superior sampling rates as compared to their conventional multi-bit counterparts. This characteristic endows one-bit signal processing frameworks with what we refer to as sample abundance. On the other hand, many signal recovery and optimization problems are formulated as (possibly non-convex) quadratic programs with linear feasibility constraints in the one-bit sampling regime. We demonstrate, with a particular focus on quadratic compressed sensing, that the sample abundance paradigm allows for the transformation of such quadratic problems to merely a linear feasibility problem by forming a large-scale overdetermined linear system; thus removing the need for costly optimization constraints and objectives. To efficiently tackle the emerging overdetermined linear feasibility problem, we further propose an enhanced randomized Kaczmarz algorithm, called Block SKM. Several numerical results are presented to illustrate the effectiveness of the proposed methodologies.

Quantized Phase-Shift Design of Active IRS for Integrated Sensing and Communications

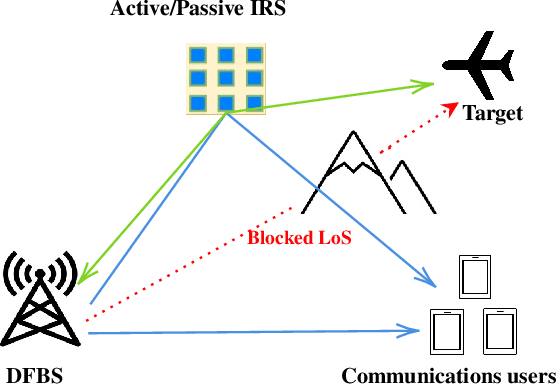
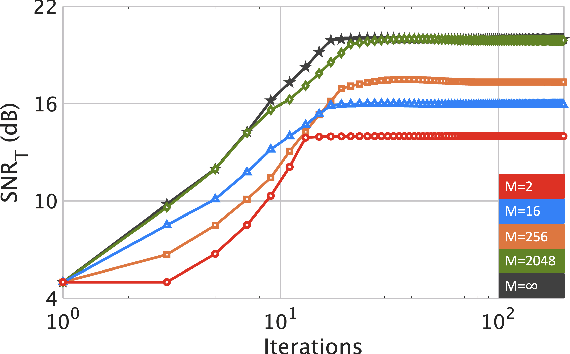
Integrated sensing and communications (ISAC) is a spectrum-sharing paradigm that allows different users to jointly utilize and access the crowded electromagnetic spectrum. In this context, intelligent reflecting surfaces (IRSs) have lately emerged as an enabler for non-line-of-sight (NLoS) ISAC. Prior IRS-aided ISAC studies assume passive surfaces and rely on the continuous-valued phase shift model. In practice, the phase-shifts are quantized. Moreover, recent research has shown substantial performance benefits with active IRS. In this paper, we include these characteristics in our IRS-aided ISAC model to maximize the receive radar and communications signal-to-noise ratios (SNR) subjected to a unimodular IRS phase-shift vector and power budget. The resulting optimization is a highly non-convex unimodular quartic optimization problem. We tackle this via a bi-quadratic transformation to split the problem into two quadratic sub-problems that are solved using the power iteration method. The proposed approach employs the M-ary unimodular sequence design via relaxed power method-like iteration (MaRLI) to design the quantized phase-shifts. As expected, numerical experiments demonstrate that our active IRS-ISAC system design with MaRLI converges to a higher value of SNR when we increase the number of IRS quantization bits.

Near-Field Low-WISL Unimodular Waveform Design for Terahertz Automotive Radar

Conventional sensing applications rely on electromagnetic far-field channel models with plane wave propagation. However, recent ultra-short-range automotive radar applications at upper millimeter-wave or low terahertz (THz) frequencies envisage operation in the near-field region, where the wavefront is spherical. Unlike far-field, the near-field beampattern is dependent on both range and angle, thus requiring a different approach to waveform design. For the first time in the literature, we adopt the beampattern matching approach to design unimodular waveforms for THz automotive radars with low weighted integrated sidelobe levels (WISL). We formulate this problem as a unimodular bi-quadratic matrix program, and solve its constituent quadratic sub-problems using our cyclic power method-like iterations (CyPMLI) algorithm. Numerical experiments demonstrate that the CyPMLI approach yields the required beampattern with low autocorrelation levels.