Phase Retrieval for Radar Waveform Design

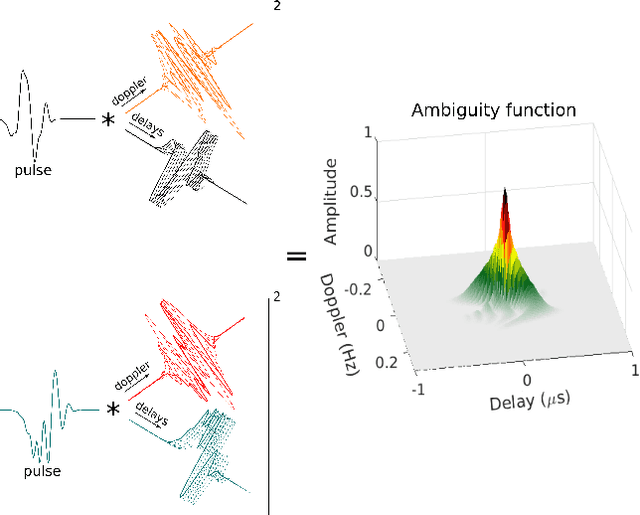
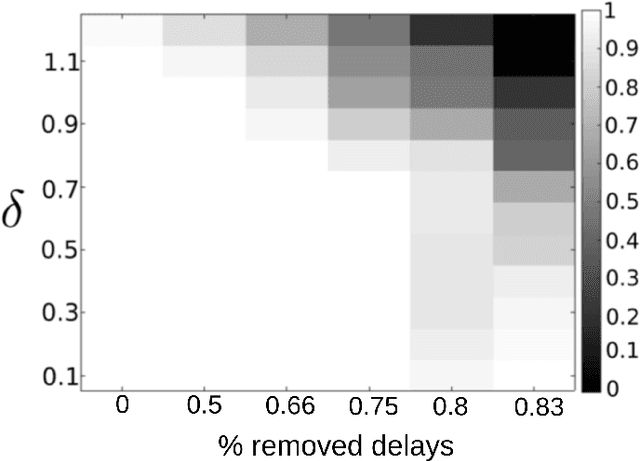
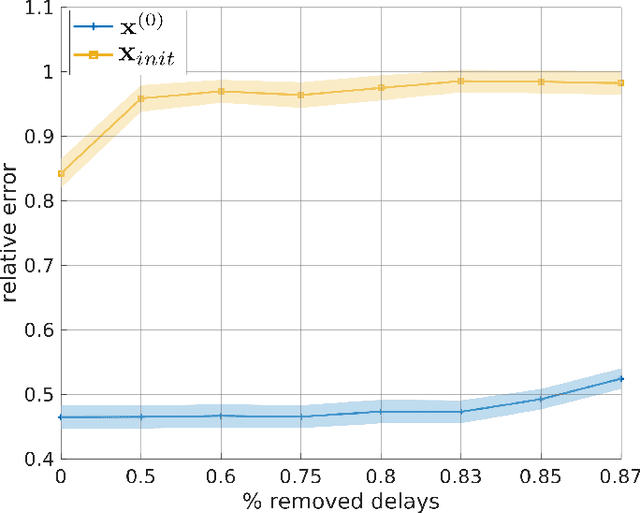
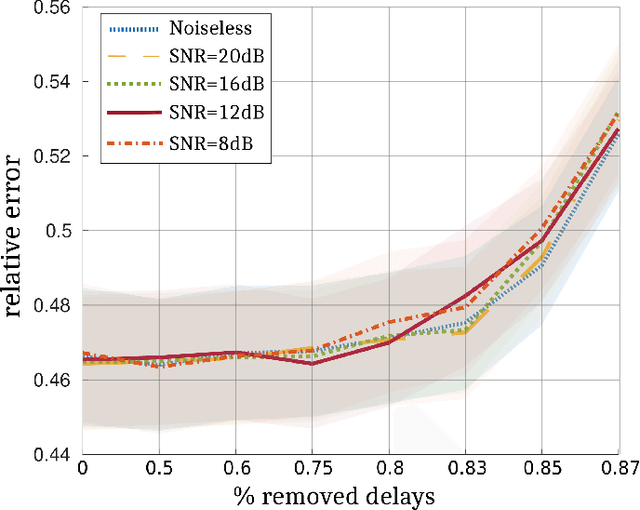
The ability of a radar to discriminate in both range and Doppler velocity is completely characterized by the ambiguity function (AF) of its transmit waveform. Mathematically, it is obtained by correlating the waveform with its Doppler-shifted and delayed replicas. We consider the inverse problem of designing a radar transmit waveform that satisfies the specified AF magnitude. This process can be viewed as a signal reconstruction with some variation of phase retrieval methods. We provide a trust-region algorithm that minimizes a smoothed non-convex least-squares objective function to iteratively recover the underlying signal-of-interest for either time- or band-limited support. The method first approximates the signal using an iterative spectral algorithm and then refines the attained initialization based upon a sequence of gradient iterations. Our theoretical analysis shows that unique signal reconstruction is possible using signal samples no more than thrice the number of signal frequencies or time samples. Numerical experiments demonstrate that our method recovers both time- and band-limited signals from even sparsely and randomly sampled AFs with mean-square-error of $1\times 10^{-6}$ and $9\times 10^{-2}$ for the full noiseless samples and sparse noisy samples, respectively.