Non-Convex Recovery from Phaseless Low-Resolution Blind Deconvolution Measurements using Noisy Masked Patterns
Paper and Code
Dec 04, 2021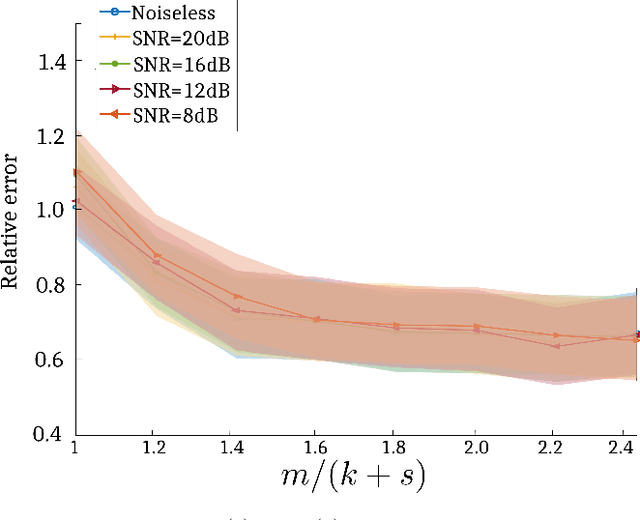
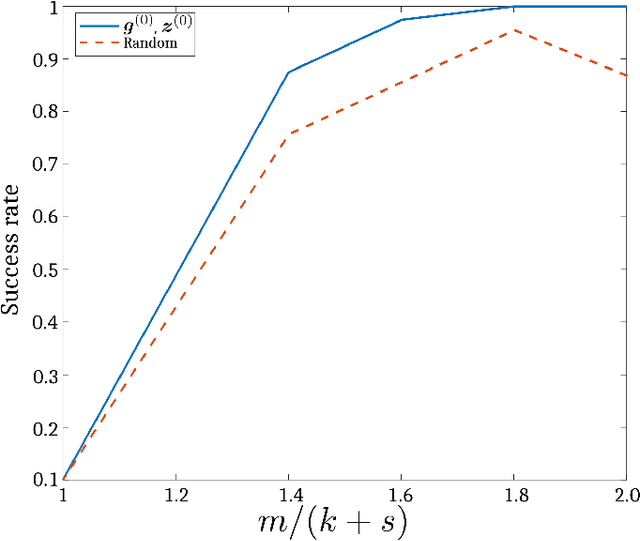
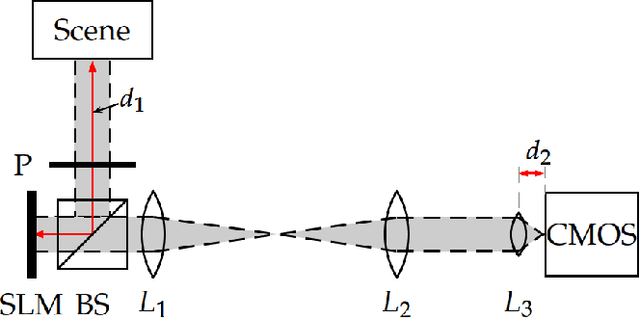

This paper addresses recovery of a kernel $\boldsymbol{h}\in \mathbb{C}^{n}$ and a signal $\boldsymbol{x}\in \mathbb{C}^{n}$ from the low-resolution phaseless measurements of their noisy circular convolution $\boldsymbol{y} = \left \rvert \boldsymbol{F}_{lo}( \boldsymbol{x}\circledast \boldsymbol{h}) \right \rvert^{2} + \boldsymbol{\eta}$, where $\boldsymbol{F}_{lo}\in \mathbb{C}^{m\times n}$ stands for a partial discrete Fourier transform ($m<n$), $\boldsymbol{\eta}$ models the noise, and $\lvert \cdot \rvert$ is the element-wise absolute value function. This problem is severely ill-posed because both the kernel and signal are unknown and, in addition, the measurements are phaseless, leading to many $\boldsymbol{x}$-$\boldsymbol{h}$ pairs that correspond to the measurements. Therefore, to guarantee a stable recovery of $\boldsymbol{x}$ and $\boldsymbol{h}$ from $\boldsymbol{y}$, we assume that the kernel $\boldsymbol{h}$ and the signal $\boldsymbol{x}$ lie in known subspaces of dimensions $k$ and $s$, respectively, such that $m\gg k+s$. We solve this problem by proposing a blind deconvolution algorithm for phaseless super-resolution (BliPhaSu) to minimize a non-convex least-squares objective function. The method first estimates a low-resolution version of both signals through a spectral algorithm, which are then refined based upon a sequence of stochastic gradient iterations. We show that our BliPhaSu algorithm converges linearly to a pair of true signals on expectation under a proper initialization that is based on spectral method. Numerical results from experimental data demonstrate perfect recovery of both $\boldsymbol{h}$ and $\boldsymbol{x}$ using our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge