On the Transformation of Latent Space in Autoencoders
Paper and Code
Jan 24, 2019

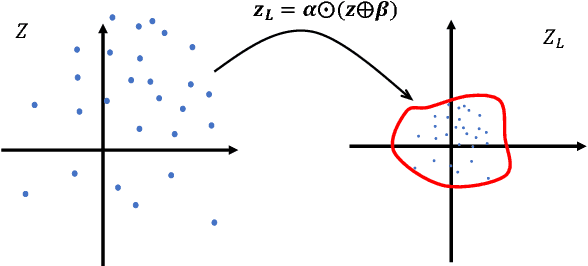

Noting the importance of the latent variables in inference and learning, we propose a novel framework for autoencoders based on the homeomorphic transformation of latent variables --- which could reduce the distance between vectors in the transformed space, while preserving the topological properties of the original space --- and investigate the effect of the transformation in both learning generative models and denoising corrupted data. The results of our experiments show that the proposed model can work as both a generative model and a denoising model with improved performance due to the transformation compared to conventional variational and denoising autoencoders.
* 9 pages and 9 figures. The paper has been submitted to ICML (The
International Conference on Machine Learning) 2019
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge