A Variance Controlled Stochastic Method with Biased Estimation for Faster Non-convex Optimization

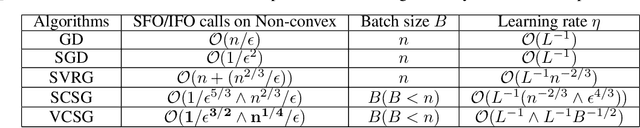
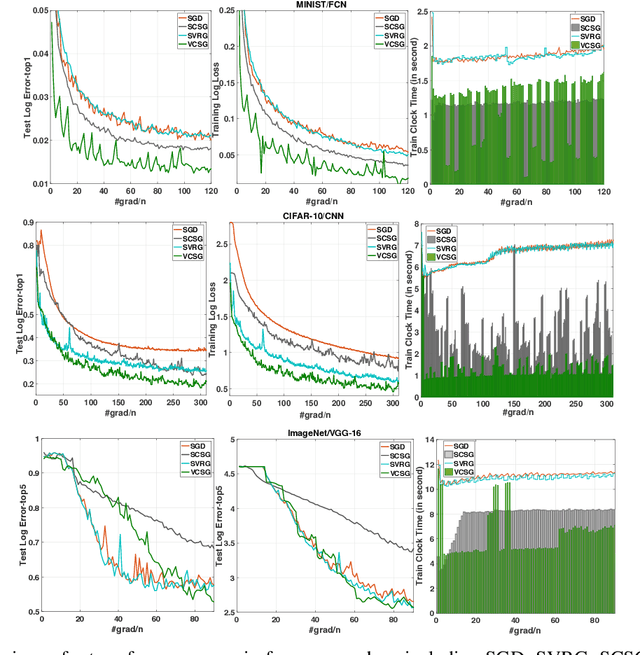
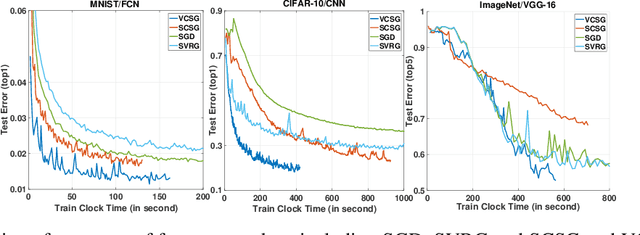
In this paper, we proposed a new technique, {\em variance controlled stochastic gradient} (VCSG), to improve the performance of the stochastic variance reduced gradient (SVRG) algorithm. To avoid over-reducing the variance of gradient by SVRG, a hyper-parameter $\lambda$ is introduced in VCSG that is able to control the reduced variance of SVRG. Theory shows that the optimization method can converge by using an unbiased gradient estimator, but in practice, biased gradient estimation can allow more efficient convergence to the vicinity since an unbiased approach is computationally more expensive. $\lambda$ also has the effect of balancing the trade-off between unbiased and biased estimations. Secondly, to minimize the number of full gradient calculations in SVRG, a variance-bounded batch is introduced to reduce the number of gradient calculations required in each iteration. For smooth non-convex functions, the proposed algorithm converges to an approximate first-order stationary point (i.e. $\mathbb{E}\|\nabla{f}(x)\|^{2}\leq\epsilon$) within $\mathcal{O}(min\{1/\epsilon^{3/2},n^{1/4}/\epsilon\})$ number of stochastic gradient evaluations, which improves the leading gradient complexity of stochastic gradient-based method SCS $(\mathcal{O}(min\{1/\epsilon^{5/3},n^{2/3}/\epsilon\})$. It is shown theoretically and experimentally that VCSG can be deployed to improve convergence.

A Stochastic Gradient Method with Biased Estimation for Faster Nonconvex Optimization

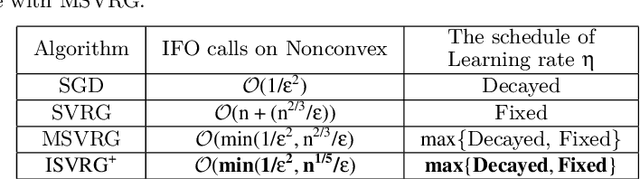
A number of optimization approaches have been proposed for optimizing nonconvex objectives (e.g. deep learning models), such as batch gradient descent, stochastic gradient descent and stochastic variance reduced gradient descent. Theory shows these optimization methods can converge by using an unbiased gradient estimator. However, in practice biased gradient estimation can allow more efficient convergence to the vicinity since an unbiased approach is computationally more expensive. To produce fast convergence there are two trade-offs of these optimization strategies which are between stochastic/batch, and between biased/unbiased. This paper proposes an integrated approach which can control the nature of the stochastic element in the optimizer and can balance the trade-off of estimator between the biased and unbiased by using a hyper-parameter. It is shown theoretically and experimentally that this hyper-parameter can be configured to provide an effective balance to improve the convergence rate.