Graph-based Nearest Neighbors with Dynamic Updates via Random Walks

Approximate nearest neighbor search (ANN) is a common way to retrieve relevant search results, especially now in the context of large language models and retrieval augmented generation. One of the most widely used algorithms for ANN is based on constructing a multi-layer graph over the dataset, called the Hierarchical Navigable Small World (HNSW). While this algorithm supports insertion of new data, it does not support deletion of existing data. Moreover, deletion algorithms described by prior work come at the cost of increased query latency, decreased recall, or prolonged deletion time. In this paper, we propose a new theoretical framework for graph-based ANN based on random walks. We then utilize this framework to analyze a randomized deletion approach that preserves hitting time statistics compared to the graph before deleting the point. We then turn this theoretical framework into a deterministic deletion algorithm, and show that it provides better tradeoff between query latency, recall, deletion time, and memory usage through an extensive collection of experiments.

Target Speaker Lipreading by Audio-Visual Self-Distillation Pretraining and Speaker Adaptation

Lipreading is an important technique for facilitating human-computer interaction in noisy environments. Our previously developed self-supervised learning method, AV2vec, which leverages multimodal self-distillation, has demonstrated promising performance in speaker-independent lipreading on the English LRS3 dataset. However, AV2vec faces challenges such as high training costs and a potential scarcity of audio-visual data for lipreading in languages other than English, such as Chinese. Additionally, most studies concentrate on speakerindependent lipreading models, which struggle to account for the substantial variation in speaking styles across di?erent speakers. To address these issues, we propose a comprehensive approach. First, we investigate cross-lingual transfer learning, adapting a pre-trained AV2vec model from a source language and optimizing it for the lipreading task in a target language. Second, we enhance the accuracy of lipreading for specific target speakers through a speaker adaptation strategy, which is not extensively explored in previous research. Third, after analyzing the complementary performance of lipreading with lip region-of-interest (ROI) and face inputs, we introduce a model ensembling strategy that integrates both, signi?cantly boosting model performance. Our method achieved a character error rate (CER) of 77.3% on the evaluation set of the ChatCLR dataset, which is lower than the top result from the 2024 Chat-scenario Chinese Lipreading Challenge.

On Differentially Private String Distances

Given a database of bit strings $A_1,\ldots,A_m\in \{0,1\}^n$, a fundamental data structure task is to estimate the distances between a given query $B\in \{0,1\}^n$ with all the strings in the database. In addition, one might further want to ensure the integrity of the database by releasing these distance statistics in a secure manner. In this work, we propose differentially private (DP) data structures for this type of tasks, with a focus on Hamming and edit distance. On top of the strong privacy guarantees, our data structures are also time- and space-efficient. In particular, our data structure is $\epsilon$-DP against any sequence of queries of arbitrary length, and for any query $B$ such that the maximum distance to any string in the database is at most $k$, we output $m$ distance estimates. Moreover, - For Hamming distance, our data structure answers any query in $\widetilde O(mk+n)$ time and each estimate deviates from the true distance by at most $\widetilde O(k/e^{\epsilon/\log k})$; - For edit distance, our data structure answers any query in $\widetilde O(mk^2+n)$ time and each estimate deviates from the true distance by at most $\widetilde O(k/e^{\epsilon/(\log k \log n)})$. For moderate $k$, both data structures support sublinear query operations. We obtain these results via a novel adaptation of the randomized response technique as a bit flipping procedure, applied to the sketched strings.

Log-concave Sampling over a Convex Body with a Barrier: a Robust and Unified Dikin Walk

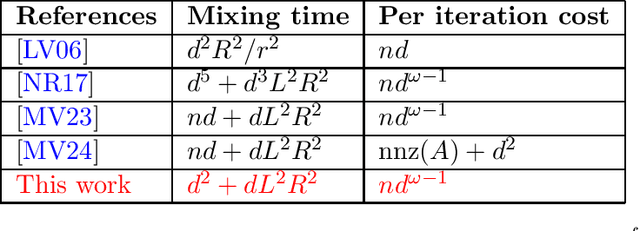
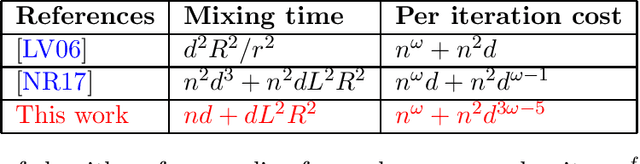
We consider the problem of sampling from a $d$-dimensional log-concave distribution $\pi(\theta) \propto \exp(-f(\theta))$ for $L$-Lipschitz $f$, constrained to a convex body with an efficiently computable self-concordant barrier function, contained in a ball of radius $R$ with a $w$-warm start. We propose a \emph{robust} sampling framework that computes spectral approximations to the Hessian of the barrier functions in each iteration. We prove that for polytopes that are described by $n$ hyperplanes, sampling with the Lee-Sidford barrier function mixes within $\widetilde O((d^2+dL^2R^2)\log(w/\delta))$ steps with a per step cost of $\widetilde O(nd^{\omega-1})$, where $\omega\approx 2.37$ is the fast matrix multiplication exponent. Compared to the prior work of Mangoubi and Vishnoi, our approach gives faster mixing time as we are able to design a generalized soft-threshold Dikin walk beyond log-barrier. We further extend our result to show how to sample from a $d$-dimensional spectrahedron, the constrained set of a semidefinite program, specified by the set $\{x\in \mathbb{R}^d: \sum_{i=1}^d x_i A_i \succeq C \}$ where $A_1,\ldots,A_d, C$ are $n\times n$ real symmetric matrices. We design a walk that mixes in $\widetilde O((nd+dL^2R^2)\log(w/\delta))$ steps with a per iteration cost of $\widetilde O(n^\omega+n^2d^{3\omega-5})$. We improve the mixing time bound of prior best Dikin walk due to Narayanan and Rakhlin that mixes in $\widetilde O((n^2d^3+n^2dL^2R^2)\log(w/\delta))$ steps.

Solving Attention Kernel Regression Problem via Pre-conditioner

Large language models have shown impressive performance in many tasks. One of the major features from the computation perspective is computing the attention matrix. Previous works [Zandieh, Han, Daliri, and Karba 2023, Alman and Song 2023] have formally studied the possibility and impossibility of approximating the attention matrix. In this work, we define and study a new problem which is called the attention kernel regression problem. We show how to solve the attention kernel regression in the input sparsity time of the data matrix.

A Nearly-Linear Time Algorithm for Structured Support Vector Machines

Quadratic programming is a fundamental problem in the field of convex optimization. Many practical tasks can be formulated as quadratic programming, for example, the support vector machine (SVM). Linear SVM is one of the most popular tools over the last three decades in machine learning before deep learning method dominating. In general, a quadratic program has input size $\Theta(n^2)$ (where $n$ is the number of variables), thus takes $\Omega(n^2)$ time to solve. Nevertheless, quadratic programs coming from SVMs has input size $O(n)$, allowing the possibility of designing nearly-linear time algorithms. Two important classes of SVMs are programs admitting low-rank kernel factorizations and low-treewidth programs. Low-treewidth convex optimization has gained increasing interest in the past few years (e.g.~linear programming [Dong, Lee and Ye 2021] and semidefinite programming [Gu and Song 2022]). Therefore, an important open question is whether there exist nearly-linear time algorithms for quadratic programs with these nice structures. In this work, we provide the first nearly-linear time algorithm for solving quadratic programming with low-rank factorization or low-treewidth, and a small number of linear constraints. Our results imply nearly-linear time algorithms for low-treewidth or low-rank SVMs.

Efficient Alternating Minimization with Applications to Weighted Low Rank Approximation

Weighted low rank approximation is a fundamental problem in numerical linear algebra, and it has many applications in machine learning. Given a matrix $M \in \mathbb{R}^{n \times n}$, a weight matrix $W \in \mathbb{R}_{\geq 0}^{n \times n}$, a parameter $k$, the goal is to output two matrices $U, V \in \mathbb{R}^{n \times k}$ such that $\| W \circ (M - U V) \|_F$ is minimized, where $\circ$ denotes the Hadamard product. Such a problem is known to be NP-hard and even hard to approximate [RSW16]. Meanwhile, alternating minimization is a good heuristic solution for approximating weighted low rank approximation. The work [LLR16] shows that, under mild assumptions, alternating minimization does provide provable guarantees. In this work, we develop an efficient and robust framework for alternating minimization. For weighted low rank approximation, this improves the runtime of [LLR16] from $n^2 k^2$ to $n^2k$. At the heart of our work framework is a high-accuracy multiple response regression solver together with a robust analysis of alternating minimization.

Low Rank Matrix Completion via Robust Alternating Minimization in Nearly Linear Time

Given a matrix $M\in \mathbb{R}^{m\times n}$, the low rank matrix completion problem asks us to find a rank-$k$ approximation of $M$ as $UV^\top$ for $U\in \mathbb{R}^{m\times k}$ and $V\in \mathbb{R}^{n\times k}$ by only observing a few entries masked by a binary matrix $P_{\Omega}\in \{0, 1 \}^{m\times n}$. As a particular instance of the weighted low rank approximation problem, solving low rank matrix completion is known to be computationally hard even to find an approximate solution [RSW16]. However, due to its practical importance, many heuristics have been proposed for this problem. In the seminal work of Jain, Netrapalli, and Sanghavi [JNS13], they show that the alternating minimization framework provides provable guarantees for low rank matrix completion problem whenever $M$ admits an incoherent low rank factorization. Unfortunately, their algorithm requires solving two exact multiple response regressions per iteration and their analysis is non-robust as they exploit the structure of the exact solution. In this paper, we take a major step towards a more efficient and robust alternating minimization framework for low rank matrix completion. Our main result is a robust alternating minimization algorithm that can tolerate moderate errors even though the regressions are solved approximately. Consequently, we also significantly improve the running time of [JNS13] from $\widetilde{O}(mnk^2 )$ to $\widetilde{O}(mnk )$ which is nearly linear in the problem size, as verifying the low rank approximation takes $O(mnk)$ time. Our core algorithmic building block is a high accuracy regression solver that solves the regression in nearly linear time per iteration.

A Nearly-Optimal Bound for Fast Regression with $\ell_\infty$ Guarantee

Given a matrix $A\in \mathbb{R}^{n\times d}$ and a vector $b\in \mathbb{R}^n$, we consider the regression problem with $\ell_\infty$ guarantees: finding a vector $x'\in \mathbb{R}^d$ such that $ \|x'-x^*\|_\infty \leq \frac{\epsilon}{\sqrt{d}}\cdot \|Ax^*-b\|_2\cdot \|A^\dagger\|$ where $x^*=\arg\min_{x\in \mathbb{R}^d}\|Ax-b\|_2$. One popular approach for solving such $\ell_2$ regression problem is via sketching: picking a structured random matrix $S\in \mathbb{R}^{m\times n}$ with $m\ll n$ and $SA$ can be quickly computed, solve the ``sketched'' regression problem $\arg\min_{x\in \mathbb{R}^d} \|SAx-Sb\|_2$. In this paper, we show that in order to obtain such $\ell_\infty$ guarantee for $\ell_2$ regression, one has to use sketching matrices that are dense. To the best of our knowledge, this is the first user case in which dense sketching matrices are necessary. On the algorithmic side, we prove that there exists a distribution of dense sketching matrices with $m=\epsilon^{-2}d\log^3(n/\delta)$ such that solving the sketched regression problem gives the $\ell_\infty$ guarantee, with probability at least $1-\delta$. Moreover, the matrix $SA$ can be computed in time $O(nd\log n)$. Our row count is nearly-optimal up to logarithmic factors, and significantly improves the result in [Price, Song and Woodruff, ICALP'17], in which a super-linear in $d$ rows, $m=\Omega(\epsilon^{-2}d^{1+\gamma})$ for $\gamma=\Theta(\sqrt{\frac{\log\log n}{\log d}})$ is required. We also develop a novel analytical framework for $\ell_\infty$ guarantee regression that utilizes the Oblivious Coordinate-wise Embedding (OCE) property introduced in [Song and Yu, ICML'21]. Our analysis is arguably much simpler and more general than [Price, Song and Woodruff, ICALP'17], and it extends to dense sketches for tensor product of vectors.

Sketching for First Order Method: Efficient Algorithm for Low-Bandwidth Channel and Vulnerability

Sketching is one of the most fundamental tools in large-scale machine learning. It enables runtime and memory saving via randomly compressing the original large problem onto lower dimensions. In this paper, we propose a novel sketching scheme for the first order method in large-scale distributed learning setting, such that the communication costs between distributed agents are saved while the convergence of the algorithms is still guaranteed. Given gradient information in a high dimension $d$, the agent passes the compressed information processed by a sketching matrix $R\in \R^{s\times d}$ with $s\ll d$, and the receiver de-compressed via the de-sketching matrix $R^\top$ to ``recover'' the information in original dimension. Using such a framework, we develop algorithms for federated learning with lower communication costs. However, such random sketching does not protect the privacy of local data directly. We show that the gradient leakage problem still exists after applying the sketching technique by showing a specific gradient attack method. As a remedy, we prove rigorously that the algorithm will be differentially private by adding additional random noises in gradient information, which results in a both communication-efficient and differentially private first order approach for federated learning tasks. Our sketching scheme can be further generalized to other learning settings and might be of independent interest itself.