Efficient Alternating Minimization with Applications to Weighted Low Rank Approximation

Weighted low rank approximation is a fundamental problem in numerical linear algebra, and it has many applications in machine learning. Given a matrix $M \in \mathbb{R}^{n \times n}$, a weight matrix $W \in \mathbb{R}_{\geq 0}^{n \times n}$, a parameter $k$, the goal is to output two matrices $U, V \in \mathbb{R}^{n \times k}$ such that $\| W \circ (M - U V) \|_F$ is minimized, where $\circ$ denotes the Hadamard product. Such a problem is known to be NP-hard and even hard to approximate [RSW16]. Meanwhile, alternating minimization is a good heuristic solution for approximating weighted low rank approximation. The work [LLR16] shows that, under mild assumptions, alternating minimization does provide provable guarantees. In this work, we develop an efficient and robust framework for alternating minimization. For weighted low rank approximation, this improves the runtime of [LLR16] from $n^2 k^2$ to $n^2k$. At the heart of our work framework is a high-accuracy multiple response regression solver together with a robust analysis of alternating minimization.

Efficient Asynchronize Stochastic Gradient Algorithm with Structured Data

Deep learning has achieved impressive success in a variety of fields because of its good generalization. However, it has been a challenging problem to quickly train a neural network with a large number of layers. The existing works utilize the locality-sensitive hashing technique or some data structures on space partitioning to alleviate the training cost in each iteration. In this work, we try accelerating the computations in each iteration from the perspective of input data points. Specifically, for a two-layer fully connected neural network, when the training data have some special properties, e.g., Kronecker structure, each iteration can be completed in sublinear time in the data dimension.

A Nearly-Optimal Bound for Fast Regression with $\ell_\infty$ Guarantee

Given a matrix $A\in \mathbb{R}^{n\times d}$ and a vector $b\in \mathbb{R}^n$, we consider the regression problem with $\ell_\infty$ guarantees: finding a vector $x'\in \mathbb{R}^d$ such that $ \|x'-x^*\|_\infty \leq \frac{\epsilon}{\sqrt{d}}\cdot \|Ax^*-b\|_2\cdot \|A^\dagger\|$ where $x^*=\arg\min_{x\in \mathbb{R}^d}\|Ax-b\|_2$. One popular approach for solving such $\ell_2$ regression problem is via sketching: picking a structured random matrix $S\in \mathbb{R}^{m\times n}$ with $m\ll n$ and $SA$ can be quickly computed, solve the ``sketched'' regression problem $\arg\min_{x\in \mathbb{R}^d} \|SAx-Sb\|_2$. In this paper, we show that in order to obtain such $\ell_\infty$ guarantee for $\ell_2$ regression, one has to use sketching matrices that are dense. To the best of our knowledge, this is the first user case in which dense sketching matrices are necessary. On the algorithmic side, we prove that there exists a distribution of dense sketching matrices with $m=\epsilon^{-2}d\log^3(n/\delta)$ such that solving the sketched regression problem gives the $\ell_\infty$ guarantee, with probability at least $1-\delta$. Moreover, the matrix $SA$ can be computed in time $O(nd\log n)$. Our row count is nearly-optimal up to logarithmic factors, and significantly improves the result in [Price, Song and Woodruff, ICALP'17], in which a super-linear in $d$ rows, $m=\Omega(\epsilon^{-2}d^{1+\gamma})$ for $\gamma=\Theta(\sqrt{\frac{\log\log n}{\log d}})$ is required. We also develop a novel analytical framework for $\ell_\infty$ guarantee regression that utilizes the Oblivious Coordinate-wise Embedding (OCE) property introduced in [Song and Yu, ICML'21]. Our analysis is arguably much simpler and more general than [Price, Song and Woodruff, ICALP'17], and it extends to dense sketches for tensor product of vectors.

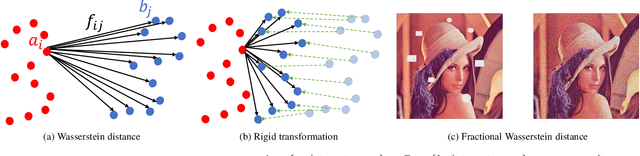
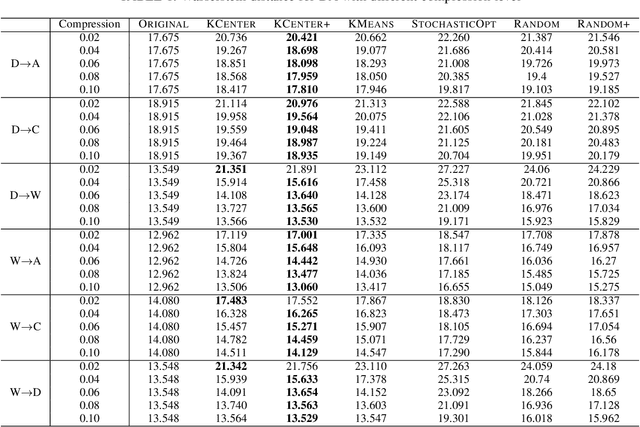
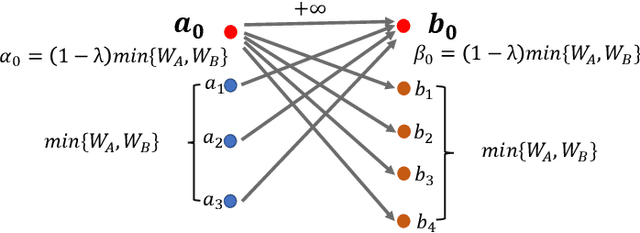
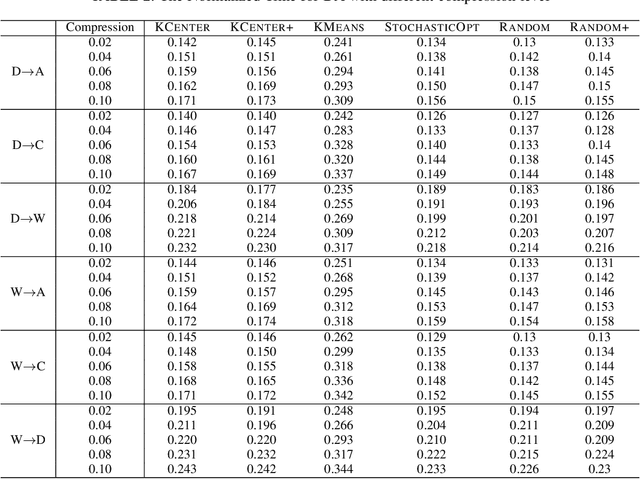
A Data-dependent Approach for High Dimensional (Robust) Wasserstein Alignment

Many real-world problems can be formulated as the alignment between two geometric patterns. Previously, a great amount of research focus on the alignment of 2D or 3D patterns in the field of computer vision. Recently, the alignment problem in high dimensions finds several novel applications in practice. However, the research is still rather limited in the algorithmic aspect. To the best of our knowledge, most existing approaches are just simple extensions of their counterparts for 2D and 3D cases, and often suffer from the issues such as high computational complexities. In this paper, we propose an effective framework to compress the high dimensional geometric patterns. Any existing alignment method can be applied to the compressed geometric patterns and the time complexity can be significantly reduced. Our idea is inspired by the observation that high dimensional data often has a low intrinsic dimension. Our framework is a "data-dependent" approach that has the complexity depending on the intrinsic dimension of the input data. Our experimental results reveal that running the alignment algorithm on compressed patterns can achieve similar qualities, comparing with the results on the original patterns, but the runtimes (including the times cost for compression) are substantially lower.

On Geometric Alignment in Low Doubling Dimension

In real-world, many problems can be formulated as the alignment between two geometric patterns. Previously, a great amount of research focus on the alignment of 2D or 3D patterns, especially in the field of computer vision. Recently, the alignment of geometric patterns in high dimension finds several novel applications, and has attracted more and more attentions. However, the research is still rather limited in terms of algorithms. To the best of our knowledge, most existing approaches for high dimensional alignment are just simple extensions of their counterparts for 2D and 3D cases, and often suffer from the issues such as high complexities. In this paper, we propose an effective framework to compress the high dimensional geometric patterns and approximately preserve the alignment quality. As a consequence, existing alignment approach can be applied to the compressed geometric patterns and thus the time complexity is significantly reduced. Our idea is inspired by the observation that high dimensional data often has a low intrinsic dimension. We adopt the widely used notion "doubling dimension" to measure the extents of our compression and the resulting approximation. Finally, we test our method on both random and real datasets, the experimental results reveal that running the alignment algorithm on compressed patterns can achieve similar qualities, comparing with the results on the original patterns, but the running times (including the times cost for compression) are substantially lower.