Relax and Merge: A Simple Yet Effective Framework for Solving Fair $k$-Means and $k$-sparse Wasserstein Barycenter Problems

The fairness of clustering algorithms has gained widespread attention across various areas, including machine learning, In this paper, we study fair $k$-means clustering in Euclidean space. Given a dataset comprising several groups, the fairness constraint requires that each cluster should contain a proportion of points from each group within specified lower and upper bounds. Due to these fairness constraints, determining the optimal locations of $k$ centers is a quite challenging task. We propose a novel ``Relax and Merge'' framework that returns a $(1+4\rho + O(\epsilon))$-approximate solution, where $\rho$ is the approximate ratio of an off-the-shelf vanilla $k$-means algorithm and $O(\epsilon)$ can be an arbitrarily small positive number. If equipped with a PTAS of $k$-means, our solution can achieve an approximation ratio of $(5+O(\epsilon))$ with only a slight violation of the fairness constraints, which improves the current state-of-the-art approximation guarantee. Furthermore, using our framework, we can also obtain a $(1+4\rho +O(\epsilon))$-approximate solution for the $k$-sparse Wasserstein Barycenter problem, which is a fundamental optimization problem in the field of optimal transport, and a $(2+6\rho)$-approximate solution for the strictly fair $k$-means clustering with no violation, both of which are better than the current state-of-the-art methods. In addition, the empirical results demonstrate that our proposed algorithm can significantly outperform baseline approaches in terms of clustering cost.

An Effective Dynamic Gradient Calibration Method for Continual Learning

Continual learning (CL) is a fundamental topic in machine learning, where the goal is to train a model with continuously incoming data and tasks. Due to the memory limit, we cannot store all the historical data, and therefore confront the ``catastrophic forgetting'' problem, i.e., the performance on the previous tasks can substantially decrease because of the missing information in the latter period. Though a number of elegant methods have been proposed, the catastrophic forgetting phenomenon still cannot be well avoided in practice. In this paper, we study the problem from the gradient perspective, where our aim is to develop an effective algorithm to calibrate the gradient in each updating step of the model; namely, our goal is to guide the model to be updated in the right direction under the situation that a large amount of historical data are unavailable. Our idea is partly inspired by the seminal stochastic variance reduction methods (e.g., SVRG and SAGA) for reducing the variance of gradient estimation in stochastic gradient descent algorithms. Another benefit is that our approach can be used as a general tool, which is able to be incorporated with several existing popular CL methods to achieve better performance. We also conduct a set of experiments on several benchmark datasets to evaluate the performance in practice.

Approximate Algorithms For $k$-Sparse Wasserstein Barycenter With Outliers

Wasserstein Barycenter (WB) is one of the most fundamental optimization problems in optimal transportation. Given a set of distributions, the goal of WB is to find a new distribution that minimizes the average Wasserstein distance to them. The problem becomes even harder if we restrict the solution to be ``$k$-sparse''. In this paper, we study the $k$-sparse WB problem in the presence of outliers, which is a more practical setting since real-world data often contains noise. Existing WB algorithms cannot be directly extended to handle the case with outliers, and thus it is urgently needed to develop some novel ideas. First, we investigate the relation between $k$-sparse WB with outliers and the clustering (with outliers) problems. In particular, we propose a clustering based LP method that yields constant approximation factor for the $k$-sparse WB with outliers problem. Further, we utilize the coreset technique to achieve the $(1+\epsilon)$-approximation factor for any $\epsilon>0$, if the dimensionality is not high. Finally, we conduct the experiments for our proposed algorithms and illustrate their efficiencies in practice.

A Novel Skip Orthogonal List for Dynamic Optimal Transport Problem

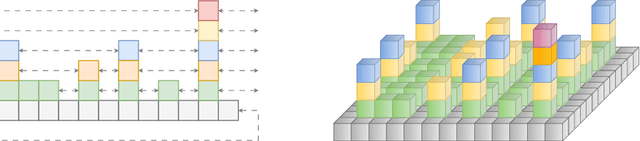
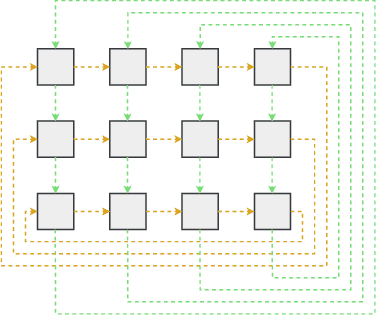
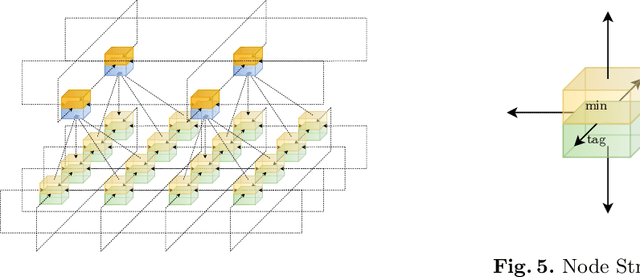
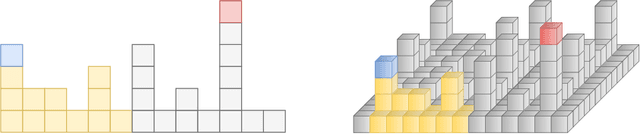
Optimal transportation is a fundamental topic that has attracted a great amount of attention from machine learning community in the past decades. In this paper, we consider an interesting discrete dynamic optimal transport problem: can we efficiently update the optimal transport plan when the weights or the locations of the data points change? This problem is naturally motivated by several applications in machine learning. For example, we often need to compute the optimal transportation cost between two different data sets; if some change happens to a few data points, should we re-compute the high complexity cost function or update the cost by some efficient dynamic data structure? We are aware that several dynamic maximum flow algorithms have been proposed before, however, the research on dynamic minimum cost flow problem is still quite limited, to the best of our knowledge. We propose a novel 2D Skip Orthogonal List together with some dynamic tree techniques. Although our algorithm is based on the conventional simplex method, it can efficiently complete each pivoting operation within $O(|V|)$ time with high probability where $V$ is the set of all supply and demand nodes. Since dynamic modifications typically do not introduce significant changes, our algorithm requires only a few simplex iterations in practice. So our algorithm is more efficient than re-computing the optimal transportation cost that needs at least one traversal over all the $O(|E|) = O(|V|^2)$ variables in general cases. Our experiments demonstrate that our algorithm significantly outperforms existing algorithms in the dynamic scenarios.

Randomized Greedy Algorithms and Composable Coreset for k-Center Clustering with Outliers

In this paper, we study the problem of {\em $k$-center clustering with outliers}. The problem has many important applications in real world, but the presence of outliers can significantly increase the computational complexity. Though a number of methods have been developed in the past decades, it is still quite challenging to design quality guaranteed algorithm with low complexity for this problem. Our idea is inspired by the greedy method, Gonzalez's algorithm, that was developed for solving the ordinary $k$-center clustering problem. Based on some novel observations, we show that a simple randomized version of this greedy strategy actually can handle outliers efficiently. We further show that this randomized greedy approach also yields small coreset for the problem in doubling metrics (even if the doubling dimension is not given), which can greatly reduce the computational complexity. Moreover, together with the partial clustering framework proposed in arXiv:1703.01539 , we prove that our coreset method can be applied to distributed data with a low communication complexity. The experimental results suggest that our algorithms can achieve near optimal solutions and yield lower complexities comparing with the existing methods.

Sublinear Time Algorithms for Several Geometric Optimization (With Outliers) Problems In Machine Learning

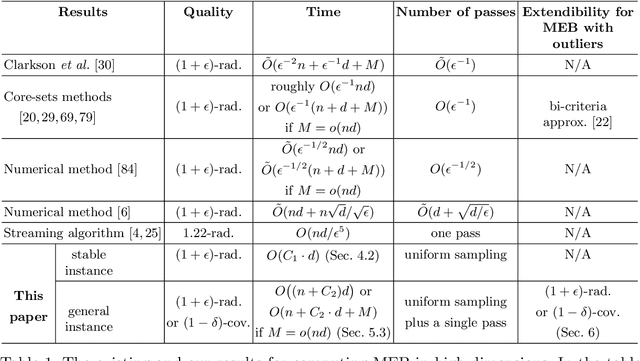
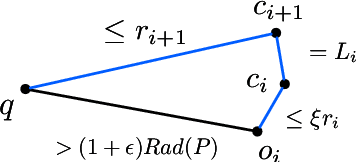
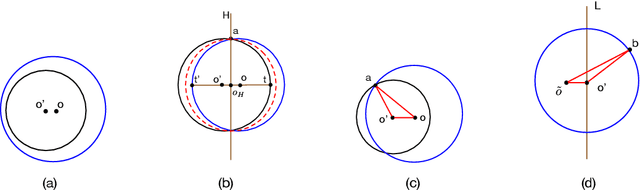
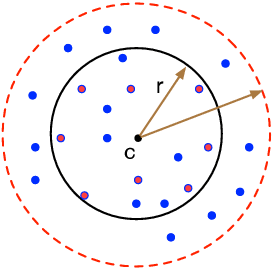
In this paper, we study several important geometric optimization problems arising in machine learning. First, we revisit the Minimum Enclosing Ball (MEB) problem in Euclidean space $\mathbb{R}^d$. The problem has been extensively studied before, but real-world machine learning tasks often need to handle large-scale datasets so that we cannot even afford linear time algorithms. Motivated by the recent studies on {\em beyond worst-case analysis}, we introduce the notion of stability for MEB, which is natural and easy to understand. Roughly speaking, an instance of MEB is stable, if the radius of the resulting ball cannot be significantly reduced by removing a small fraction of the input points. Under the stability assumption, we present two sampling algorithms for computing radius-approximate MEB with sample complexities independent of the number of input points $n$. In particular, the second algorithm has the sample complexity even independent of the dimensionality $d$. We also consider the general case without the stability assumption. We present a hybrid algorithm that can output either a radius-approximate MEB or a covering-approximate MEB. Our algorithm improves the running time and the number of passes for the previous sublinear MEB algorithms. Our method relies on two novel techniques, the Uniform-Adaptive Sampling method and Sandwich Lemma. Furthermore, we observe that these two techniques can be generalized to design sublinear time algorithms for a broader range of geometric optimization problems with outliers in high dimensions, including MEB with outliers, one-class and two-class linear SVMs with outliers, $k$-center clustering with outliers, and flat fitting with outliers. Our proposed algorithms also work fine for kernels.

Coresets for Relational Data and The Applications

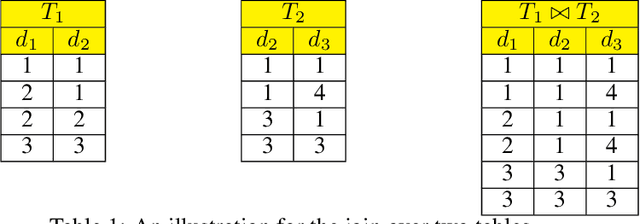
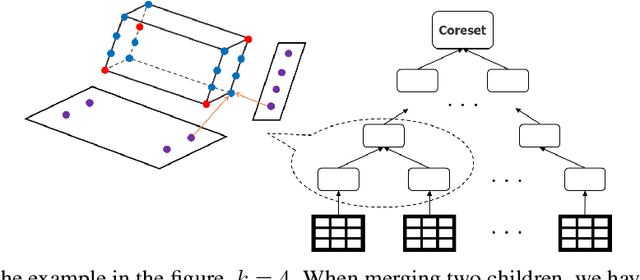
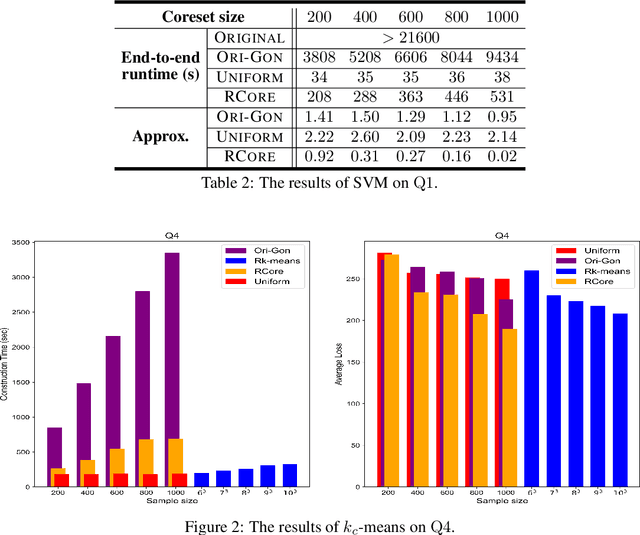
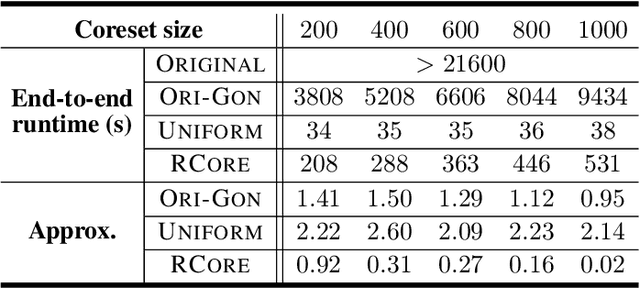
A coreset is a small set that can approximately preserve the structure of the original input data set. Therefore we can run our algorithm on a coreset so as to reduce the total computational complexity. Conventional coreset techniques assume that the input data set is available to process explicitly. However, this assumption may not hold in real-world scenarios. In this paper, we consider the problem of coresets construction over relational data. Namely, the data is decoupled into several relational tables, and it could be very expensive to directly materialize the data matrix by joining the tables. We propose a novel approach called ``aggregation tree with pseudo-cube'' that can build a coreset from bottom to up. Moreover, our approach can neatly circumvent several troublesome issues of relational learning problems [Khamis et al., PODS 2019]. Under some mild assumptions, we show that our coreset approach can be applied for the machine learning tasks, such as clustering, logistic regression and SVM.

Coresets for Wasserstein Distributionally Robust Optimization Problems

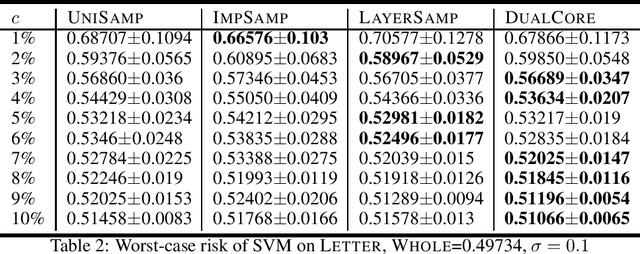
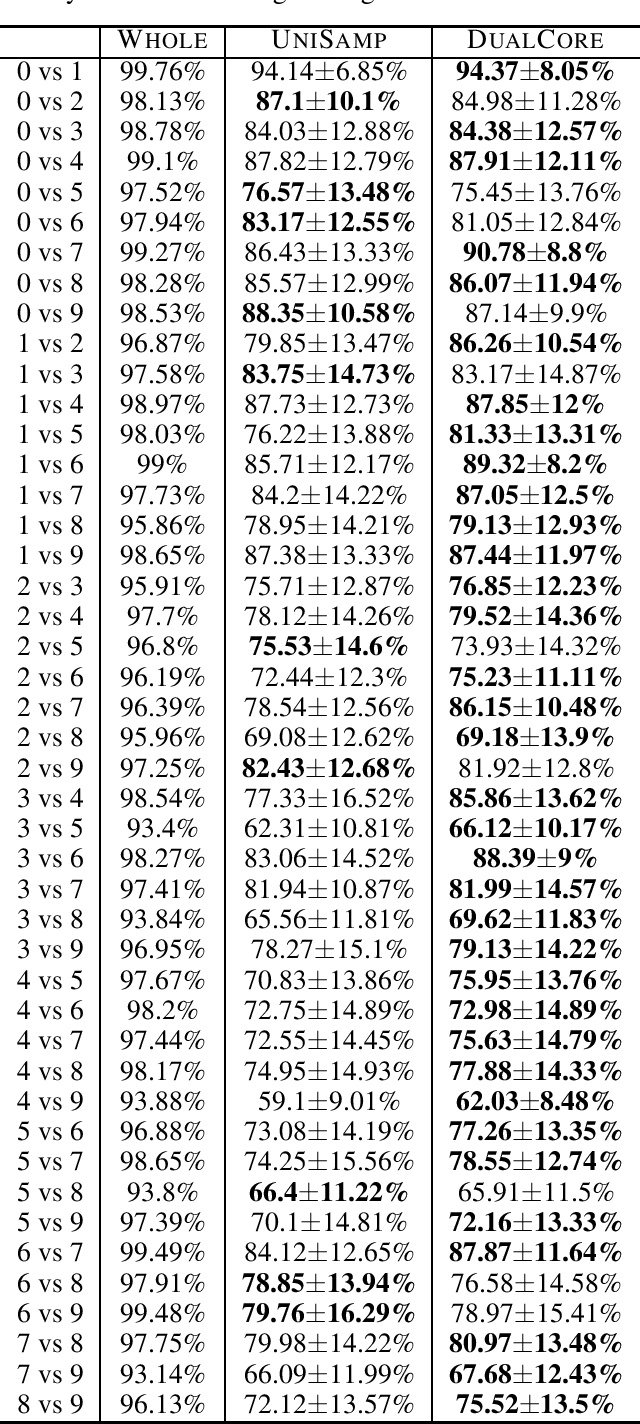
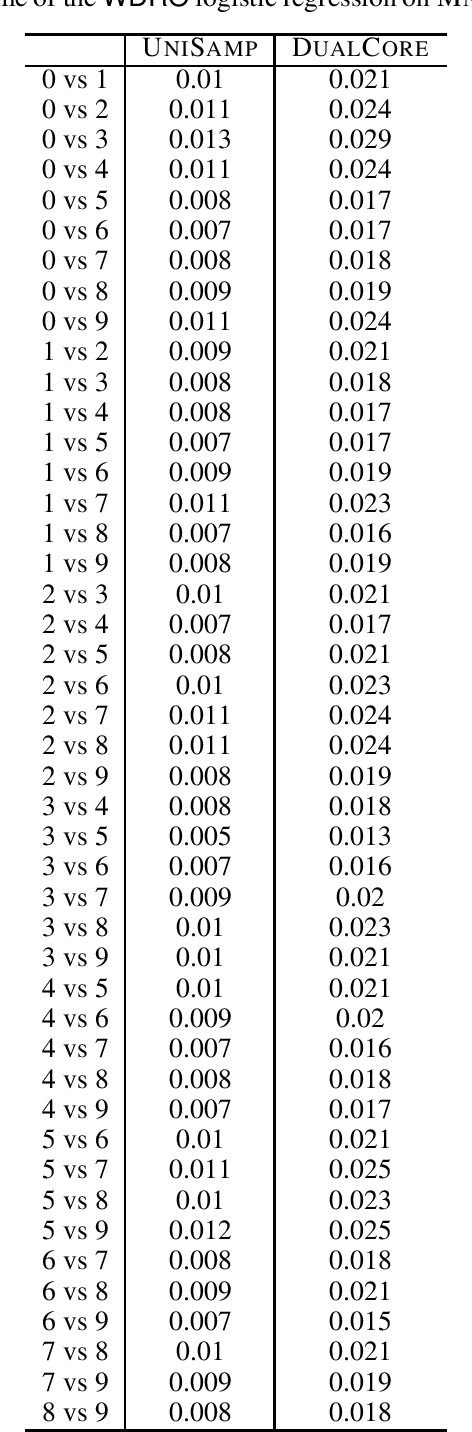
Wasserstein distributionally robust optimization (\textsf{WDRO}) is a popular model to enhance the robustness of machine learning with ambiguous data. However, the complexity of \textsf{WDRO} can be prohibitive in practice since solving its ``minimax'' formulation requires a great amount of computation. Recently, several fast \textsf{WDRO} training algorithms for some specific machine learning tasks (e.g., logistic regression) have been developed. However, the research on designing efficient algorithms for general large-scale \textsf{WDRO}s is still quite limited, to the best of our knowledge. \textit{Coreset} is an important tool for compressing large dataset, and thus it has been widely applied to reduce the computational complexities for many optimization problems. In this paper, we introduce a unified framework to construct the $\epsilon$-coreset for the general \textsf{WDRO} problems. Though it is challenging to obtain a conventional coreset for \textsf{WDRO} due to the uncertainty issue of ambiguous data, we show that we can compute a ``dual coreset'' by using the strong duality property of \textsf{WDRO}. Also, the error introduced by the dual coreset can be theoretically guaranteed for the original \textsf{WDRO} objective. To construct the dual coreset, we propose a novel grid sampling approach that is particularly suitable for the dual formulation of \textsf{WDRO}. Finally, we implement our coreset approach and illustrate its effectiveness for several \textsf{WDRO} problems in the experiments.

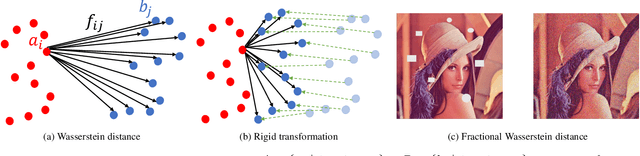
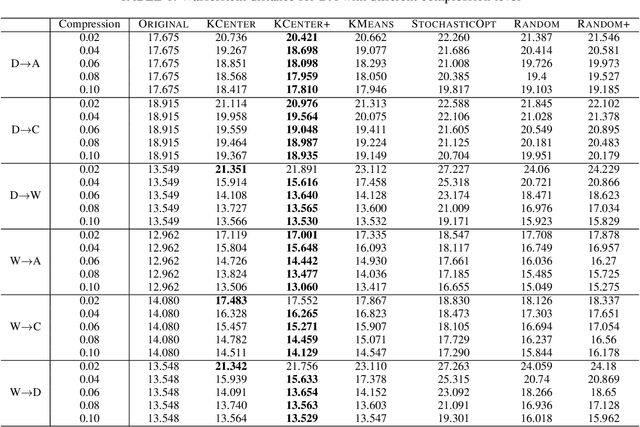
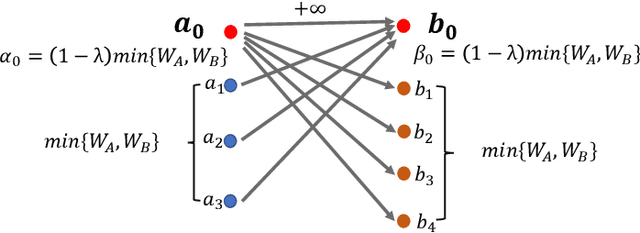
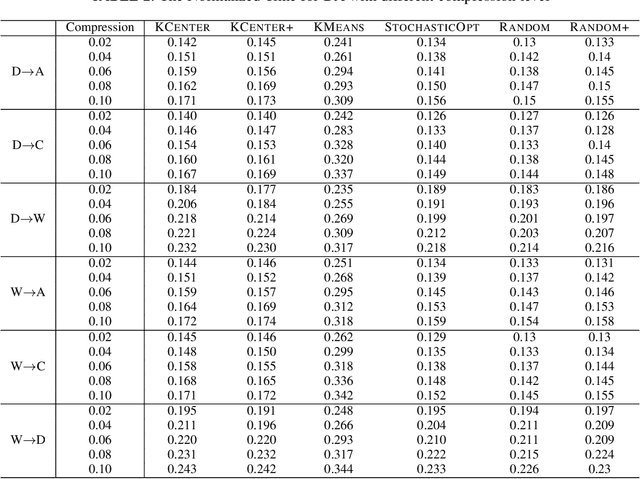
A Data-dependent Approach for High Dimensional (Robust) Wasserstein Alignment

Many real-world problems can be formulated as the alignment between two geometric patterns. Previously, a great amount of research focus on the alignment of 2D or 3D patterns in the field of computer vision. Recently, the alignment problem in high dimensions finds several novel applications in practice. However, the research is still rather limited in the algorithmic aspect. To the best of our knowledge, most existing approaches are just simple extensions of their counterparts for 2D and 3D cases, and often suffer from the issues such as high computational complexities. In this paper, we propose an effective framework to compress the high dimensional geometric patterns. Any existing alignment method can be applied to the compressed geometric patterns and the time complexity can be significantly reduced. Our idea is inspired by the observation that high dimensional data often has a low intrinsic dimension. Our framework is a "data-dependent" approach that has the complexity depending on the intrinsic dimension of the input data. Our experimental results reveal that running the alignment algorithm on compressed patterns can achieve similar qualities, comparing with the results on the original patterns, but the runtimes (including the times cost for compression) are substantially lower.

A Novel Sequential Coreset Method for Gradient Descent Algorithms

A wide range of optimization problems arising in machine learning can be solved by gradient descent algorithms, and a central question in this area is how to efficiently compress a large-scale dataset so as to reduce the computational complexity. {\em Coreset} is a popular data compression technique that has been extensively studied before. However, most of existing coreset methods are problem-dependent and cannot be used as a general tool for a broader range of applications. A key obstacle is that they often rely on the pseudo-dimension and total sensitivity bound that can be very high or hard to obtain. In this paper, based on the ''locality'' property of gradient descent algorithms, we propose a new framework, termed ''sequential coreset'', which effectively avoids these obstacles. Moreover, our method is particularly suitable for sparse optimization whence the coreset size can be further reduced to be only poly-logarithmically dependent on the dimension. In practice, the experimental results suggest that our method can save a large amount of running time compared with the baseline algorithms.