Randomized Greedy Algorithms and Composable Coreset for k-Center Clustering with Outliers

In this paper, we study the problem of {\em $k$-center clustering with outliers}. The problem has many important applications in real world, but the presence of outliers can significantly increase the computational complexity. Though a number of methods have been developed in the past decades, it is still quite challenging to design quality guaranteed algorithm with low complexity for this problem. Our idea is inspired by the greedy method, Gonzalez's algorithm, that was developed for solving the ordinary $k$-center clustering problem. Based on some novel observations, we show that a simple randomized version of this greedy strategy actually can handle outliers efficiently. We further show that this randomized greedy approach also yields small coreset for the problem in doubling metrics (even if the doubling dimension is not given), which can greatly reduce the computational complexity. Moreover, together with the partial clustering framework proposed in arXiv:1703.01539 , we prove that our coreset method can be applied to distributed data with a low communication complexity. The experimental results suggest that our algorithms can achieve near optimal solutions and yield lower complexities comparing with the existing methods.

A Practical Framework for Solving Center-Based Clustering with Outliers

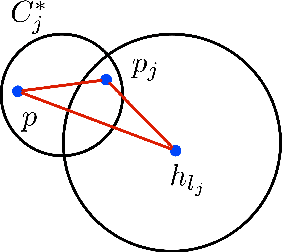
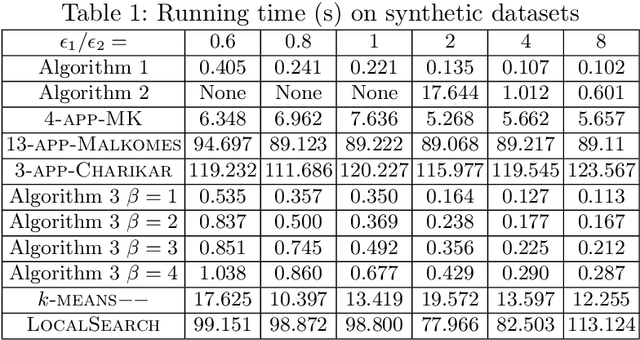
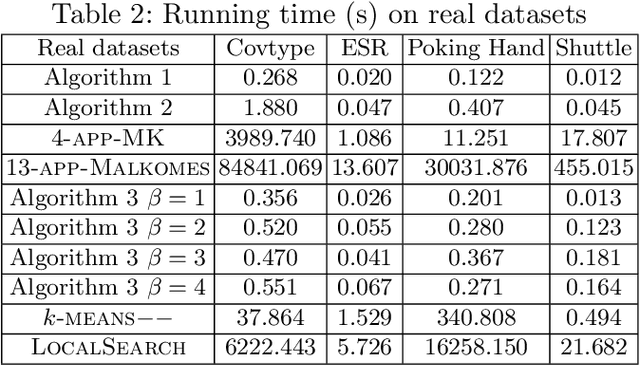
Clustering has many important applications in computer science, but real-world datasets often contain outliers. Moreover, the existence of outliers can make the clustering problems to be much more challenging. In this paper, we propose a practical framework for solving the problems of $k$-center/median/means clustering with outliers. The framework actually is very simple, where we just need to take a small sample from input and run existing approximation algorithm on the sample. However, our analysis is fundamentally different from the previous sampling based ideas. In particular, the size of the sample is independent of the input data size and dimensionality. To explain the effectiveness of random sampling in theory, we introduce a `significance' criterion and prove that the performance of our framework depends on the significance degree of the given instance. The result proposed in this paper falls under the umbrella of beyond worst-case analysis in terms of clustering with outliers. The experiments suggest that our framework can achieve comparable clustering result with existing methods, but greatly reduce the running time.