A Practical Framework for Solving Center-Based Clustering with Outliers

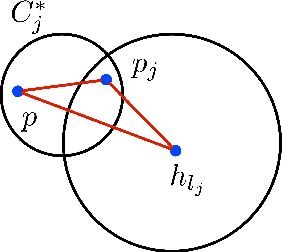
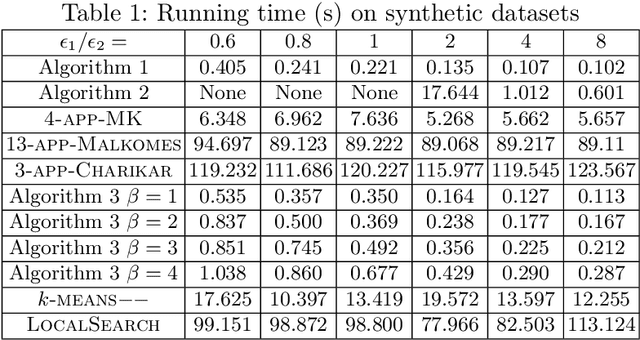
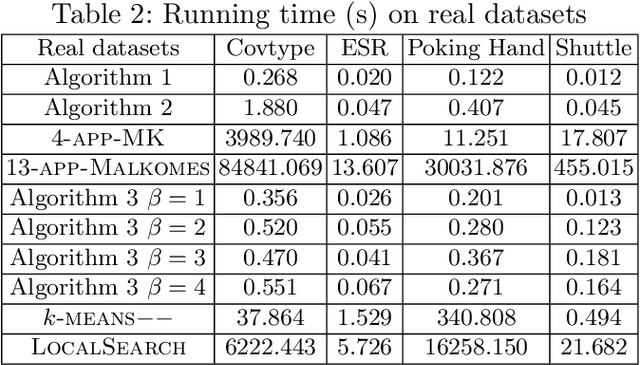
Clustering has many important applications in computer science, but real-world datasets often contain outliers. Moreover, the existence of outliers can make the clustering problems to be much more challenging. In this paper, we propose a practical framework for solving the problems of $k$-center/median/means clustering with outliers. The framework actually is very simple, where we just need to take a small sample from input and run existing approximation algorithm on the sample. However, our analysis is fundamentally different from the previous sampling based ideas. In particular, the size of the sample is independent of the input data size and dimensionality. To explain the effectiveness of random sampling in theory, we introduce a `significance' criterion and prove that the performance of our framework depends on the significance degree of the given instance. The result proposed in this paper falls under the umbrella of beyond worst-case analysis in terms of clustering with outliers. The experiments suggest that our framework can achieve comparable clustering result with existing methods, but greatly reduce the running time.