A Novel Skip Orthogonal List for Dynamic Optimal Transport Problem
Paper and Code
Oct 27, 2023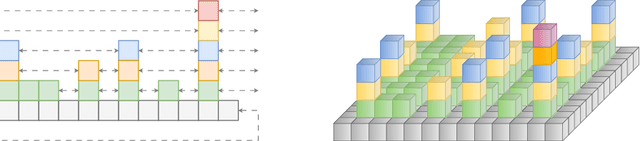
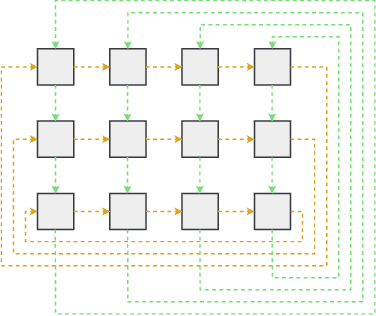
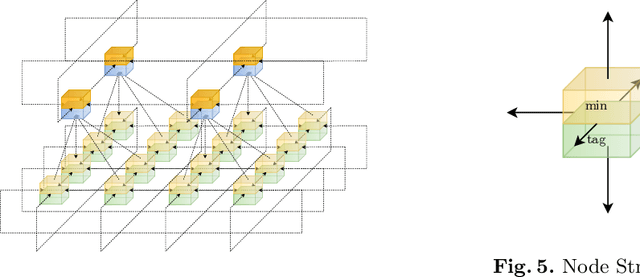
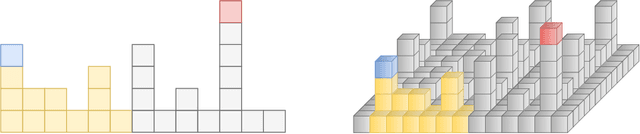
Optimal transportation is a fundamental topic that has attracted a great amount of attention from machine learning community in the past decades. In this paper, we consider an interesting discrete dynamic optimal transport problem: can we efficiently update the optimal transport plan when the weights or the locations of the data points change? This problem is naturally motivated by several applications in machine learning. For example, we often need to compute the optimal transportation cost between two different data sets; if some change happens to a few data points, should we re-compute the high complexity cost function or update the cost by some efficient dynamic data structure? We are aware that several dynamic maximum flow algorithms have been proposed before, however, the research on dynamic minimum cost flow problem is still quite limited, to the best of our knowledge. We propose a novel 2D Skip Orthogonal List together with some dynamic tree techniques. Although our algorithm is based on the conventional simplex method, it can efficiently complete each pivoting operation within $O(|V|)$ time with high probability where $V$ is the set of all supply and demand nodes. Since dynamic modifications typically do not introduce significant changes, our algorithm requires only a few simplex iterations in practice. So our algorithm is more efficient than re-computing the optimal transportation cost that needs at least one traversal over all the $O(|E|) = O(|V|^2)$ variables in general cases. Our experiments demonstrate that our algorithm significantly outperforms existing algorithms in the dynamic scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge