Functional-level Uncertainty Quantification for Calibrated Fine-tuning on LLMs

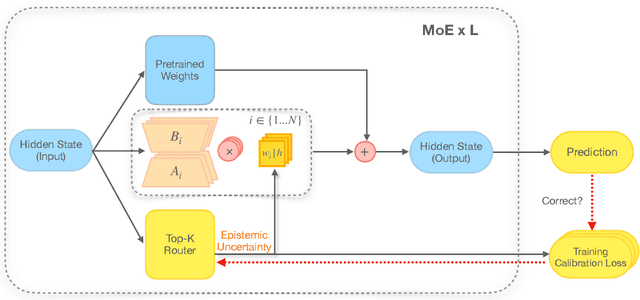
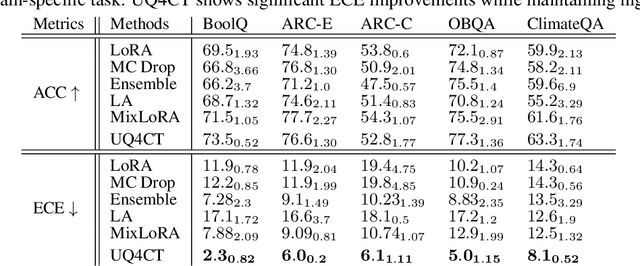
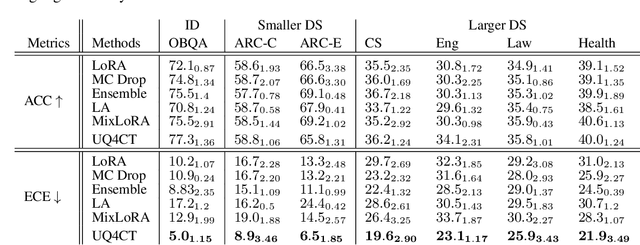
From common-sense reasoning to domain-specific tasks, parameter-efficient fine tuning (PEFT) methods for large language models (LLMs) have showcased significant performance improvements on downstream tasks. However, fine-tuned LLMs often struggle with overconfidence in uncertain predictions, particularly due to sparse training data. This overconfidence reflects poor epistemic uncertainty calibration, which arises from limitations in the model's ability to generalize with limited data. Existing PEFT uncertainty quantification methods for LLMs focus on the post fine-tuning stage and thus have limited capability in calibrating epistemic uncertainty. To address these limitations, we propose Functional-Level Uncertainty Quantification for Calibrated Fine-Tuning (UQ4CT), which captures and calibrates functional-level epistemic uncertainty during the fine-tuning stage via a mixture-of-expert framework. We show that UQ4CT reduces Expected Calibration Error (ECE) by more than $25\%$ while maintaining high accuracy across $5$ benchmarks. Furthermore, UQ4CT maintains superior ECE performance with high accuracy under distribution shift, showcasing improved generalizability.

Diff-BBO: Diffusion-Based Inverse Modeling for Black-Box Optimization

Black-box optimization (BBO) aims to optimize an objective function by iteratively querying a black-box oracle. This process demands sample-efficient optimization due to the high computational cost of function evaluations. While prior studies focus on forward approaches to learn surrogates for the unknown objective function, they struggle with high-dimensional inputs where valid inputs form a small subspace (e.g., valid protein sequences), which is common in real-world tasks. Recently, diffusion models have demonstrated impressive capability in learning the high-dimensional data manifold. They have shown promising performance in black-box optimization tasks but only in offline settings. In this work, we propose diffusion-based inverse modeling for black-box optimization (Diff-BBO), the first inverse approach leveraging diffusion models for online BBO problem. Diff-BBO distinguishes itself from forward approaches through the design of acquisition function. Instead of proposing candidates in the design space, Diff-BBO employs a novel acquisition function Uncertainty-aware Exploration (UaE) to propose objective function values, which leverages the uncertainty of a conditional diffusion model to generate samples in the design space. Theoretically, we prove that using UaE leads to optimal optimization outcomes. Empirically, we redesign experiments on the Design-Bench benchmark for online settings and show that Diff-BBO achieves state-of-the-art performance.

Multi-Fidelity Residual Neural Processes for Scalable Surrogate Modeling

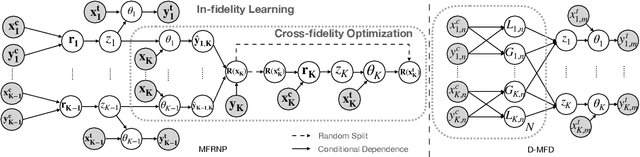
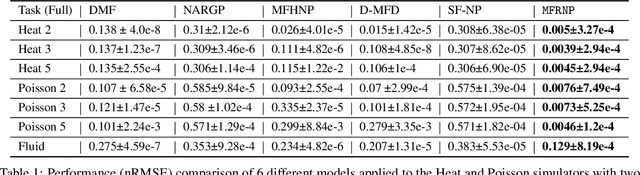
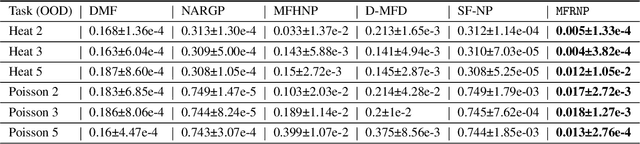
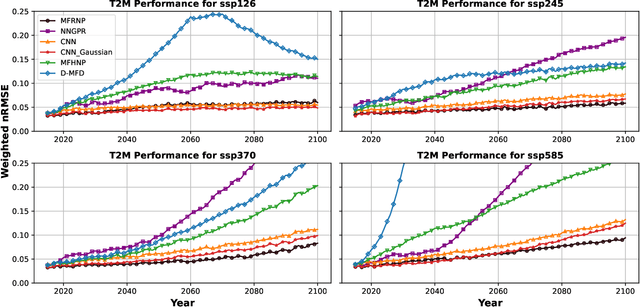
Multi-fidelity surrogate modeling aims to learn an accurate surrogate at the highest fidelity level by combining data from multiple sources. Traditional methods relying on Gaussian processes can hardly scale to high-dimensional data. Deep learning approaches utilize neural network based encoders and decoders to improve scalability. These approaches share encoded representations across fidelities without including corresponding decoder parameters. At the highest fidelity, the representations are decoded with different parameters, making the shared information inherently inaccurate. This hinders inference performance, especially in out-of-distribution scenarios when the highest fidelity data has limited domain coverage. To address these limitations, we propose Multi-fidelity Residual Neural Processes (MFRNP), a novel multi-fidelity surrogate modeling framework. MFRNP optimizes lower fidelity decoders for accurate information sharing by aggregating lower fidelity surrogate outputs and models residual between the aggregation and ground truth on the highest fidelity. We show that MFRNP significantly outperforms current state-of-the-art in learning partial differential equations and a real-world climate modeling task.

Disentangled Multi-Fidelity Deep Bayesian Active Learning

To balance quality and cost, various domain areas of science and engineering run simulations at multiple levels of sophistication. Multi-fidelity active learning aims to learn a direct mapping from input parameters to simulation outputs by actively acquiring data from multiple fidelity levels. However, existing approaches based on Gaussian processes are hardly scalable to high-dimensional data. Other deep learning-based methods use the hierarchical structure, which only supports passing information from low-fidelity to high-fidelity. This approach also leads to the undesirable propagation of errors from low-fidelity representations to high-fidelity ones. We propose a novel disentangled deep Bayesian learning framework for multi-fidelity active learning, that learns the surrogate models conditioned on the distribution of functions at multiple fidelities.