Layer-Adaptive State Pruning for Deep State Space Models

Due to the lack of state dimension optimization methods, deep state space models (SSMs) have sacrificed model capacity, training search space, or stability to alleviate computational costs caused by high state dimensions. In this work, we provide a structured pruning method for SSMs, Layer-Adaptive STate pruning (LAST), which reduces the state dimension of each layer in minimizing model-level energy loss by extending modal truncation for a single system. LAST scores are evaluated using $\mathcal{H}_{\infty}$ norms of subsystems for each state and layer-wise energy normalization. The scores serve as global pruning criteria, enabling cross-layer comparison of states and layer-adaptive pruning. Across various sequence benchmarks, LAST optimizes previous SSMs, revealing the redundancy and compressibility of their state spaces. Notably, we demonstrate that, on average, pruning 33% of states still maintains performance with 0.52% accuracy loss in multi-input multi-output SSMs without retraining. Code is available at $\href{https://github.com/msgwak/LAST}{\text{this https URL}}$.

Demystifying SGD with Doubly Stochastic Gradients

Optimization objectives in the form of a sum of intractable expectations are rising in importance (e.g., diffusion models, variational autoencoders, and many more), a setting also known as "finite sum with infinite data." For these problems, a popular strategy is to employ SGD with doubly stochastic gradients (doubly SGD): the expectations are estimated using the gradient estimator of each component, while the sum is estimated by subsampling over these estimators. Despite its popularity, little is known about the convergence properties of doubly SGD, except under strong assumptions such as bounded variance. In this work, we establish the convergence of doubly SGD with independent minibatching and random reshuffling under general conditions, which encompasses dependent component gradient estimators. In particular, for dependent estimators, our analysis allows fined-grained analysis of the effect correlations. As a result, under a per-iteration computational budget of $b \times m$, where $b$ is the minibatch size and $m$ is the number of Monte Carlo samples, our analysis suggests where one should invest most of the budget in general. Furthermore, we prove that random reshuffling (RR) improves the complexity dependence on the subsampling noise.

A Gated MLP Architecture for Learning Topological Dependencies in Spatio-Temporal Graphs

Graph Neural Networks (GNNs) and Transformer have been increasingly adopted to learn the complex vector representations of spatio-temporal graphs, capturing intricate spatio-temporal dependencies crucial for applications such as traffic datasets. Although many existing methods utilize multi-head attention mechanisms and message-passing neural networks (MPNNs) to capture both spatial and temporal relations, these approaches encode temporal and spatial relations independently, and reflect the graph's topological characteristics in a limited manner. In this work, we introduce the Cycle to Mixer (Cy2Mixer), a novel spatio-temporal GNN based on topological non-trivial invariants of spatio-temporal graphs with gated multi-layer perceptrons (gMLP). The Cy2Mixer is composed of three blocks based on MLPs: A message-passing block for encapsulating spatial information, a cycle message-passing block for enriching topological information through cyclic subgraphs, and a temporal block for capturing temporal properties. We bolster the effectiveness of Cy2Mixer with mathematical evidence emphasizing that our cycle message-passing block is capable of offering differentiated information to the deep learning model compared to the message-passing block. Furthermore, empirical evaluations substantiate the efficacy of the Cy2Mixer, demonstrating state-of-the-art performances across various traffic benchmark datasets.

Provably Scalable Black-Box Variational Inference with Structured Variational Families

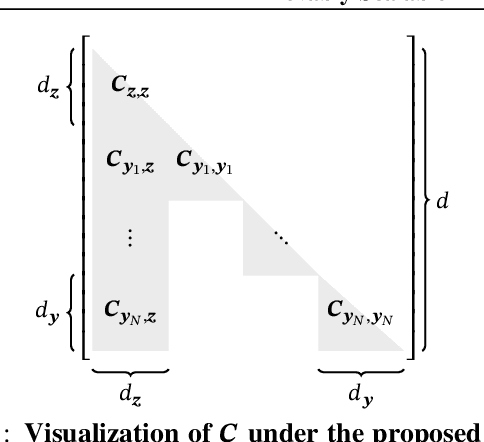
Variational families with full-rank covariance approximations are known not to work well in black-box variational inference (BBVI), both empirically and theoretically. In fact, recent computational complexity results for BBVI have established that full-rank variational families scale poorly with the dimensionality of the problem compared to e.g. mean field families. This is particularly critical to hierarchical Bayesian models with local variables; their dimensionality increases with the size of the datasets. Consequently, one gets an iteration complexity with an explicit $\mathcal{O}(N^2)$ dependence on the dataset size $N$. In this paper, we explore a theoretical middle ground between mean-field variational families and full-rank families: structured variational families. We rigorously prove that certain scale matrix structures can achieve a better iteration complexity of $\mathcal{O}(N)$, implying better scaling with respect to $N$. We empirically verify our theoretical results on large-scale hierarchical models.

Modeling Choice via Self-Attention

Models of choice are a fundamental input to many now-canonical optimization problems in the field of Operations Management, including assortment, inventory, and price optimization. Naturally, accurate estimation of these models from data is a critical step in the application of these optimization problems in practice, and so it is perhaps surprising that such choice estimation has to now been accomplished almost exclusively, both in theory and in practice, (a) without the use of deep learning in any meaningful way, and (b) via evaluation on limited data with constantly-changing metrics. This is in stark contrast to the vast majority of similar learning applications, for which the practice of machine learning suggests that (a) neural network-based models are typically state-of-the-art, and (b) strict standardization on evaluation procedures (datasets, metrics, etc.) is crucial. Thus motivated, we first propose a choice model that is the first to successfully (both theoretically and practically) leverage a modern neural network architectural concept (self-attention). Theoretically, we show that our attention-based choice model is a low-rank generalization of the Halo Multinomial Logit model, a recent model that parsimoniously captures irrational choice effects and has seen empirical success. We prove that whereas the Halo-MNL requires $\Omega(m^2)$ data samples to estimate, where $m$ is the number of products, our model supports a natural nonconvex estimator (in particular, that which a standard neural network implementation would apply) which admits a near-optimal stationary point with $O(m)$ samples. We then establish the first realistic-scale benchmark for choice estimation on real data and use this benchmark to run the largest evaluation of existing choice models to date. We find that the model we propose is dominant over both short-term and long-term data periods.

Learning to Scale Logits for Temperature-Conditional GFlowNets

GFlowNets are probabilistic models that learn a stochastic policy that sequentially generates compositional structures, such as molecular graphs. They are trained with the objective of sampling such objects with probability proportional to the object's reward. Among GFlowNets, the temperature-conditional GFlowNets represent a family of policies indexed by temperature, and each is associated with the correspondingly tempered reward function. The major benefit of temperature-conditional GFlowNets is the controllability of GFlowNets' exploration and exploitation through adjusting temperature. We propose Learning to Scale Logits for temperature-conditional GFlowNets (LSL-GFN), a novel architectural design that greatly accelerates the training of temperature-conditional GFlowNets. It is based on the idea that previously proposed temperature-conditioning approaches introduced numerical challenges in the training of the deep network because different temperatures may give rise to very different gradient profiles and ideal scales of the policy's logits. We find that the challenge is greatly reduced if a learned function of the temperature is used to scale the policy's logits directly. We empirically show that our strategy dramatically improves the performances of GFlowNets, outperforming other baselines, including reinforcement learning and sampling methods, in terms of discovering diverse modes in multiple biochemical tasks.