Topology-Informed Graph Transformer

Transformers have revolutionized performance in Natural Language Processing and Vision, paving the way for their integration with Graph Neural Networks (GNNs). One key challenge in enhancing graph transformers is strengthening the discriminative power of distinguishing isomorphisms of graphs, which plays a crucial role in boosting their predictive performances. To address this challenge, we introduce 'Topology-Informed Graph Transformer (TIGT)', a novel transformer enhancing both discriminative power in detecting graph isomorphisms and the overall performance of Graph Transformers. TIGT consists of four components: A topological positional embedding layer using non-isomorphic universal covers based on cyclic subgraphs of graphs to ensure unique graph representation: A dual-path message-passing layer to explicitly encode topological characteristics throughout the encoder layers: A global attention mechanism: And a graph information layer to recalibrate channel-wise graph features for better feature representation. TIGT outperforms previous Graph Transformers in classifying synthetic dataset aimed at distinguishing isomorphism classes of graphs. Additionally, mathematical analysis and empirical evaluations highlight our model's competitive edge over state-of-the-art Graph Transformers across various benchmark datasets.

A Gated MLP Architecture for Learning Topological Dependencies in Spatio-Temporal Graphs

Graph Neural Networks (GNNs) and Transformer have been increasingly adopted to learn the complex vector representations of spatio-temporal graphs, capturing intricate spatio-temporal dependencies crucial for applications such as traffic datasets. Although many existing methods utilize multi-head attention mechanisms and message-passing neural networks (MPNNs) to capture both spatial and temporal relations, these approaches encode temporal and spatial relations independently, and reflect the graph's topological characteristics in a limited manner. In this work, we introduce the Cycle to Mixer (Cy2Mixer), a novel spatio-temporal GNN based on topological non-trivial invariants of spatio-temporal graphs with gated multi-layer perceptrons (gMLP). The Cy2Mixer is composed of three blocks based on MLPs: A message-passing block for encapsulating spatial information, a cycle message-passing block for enriching topological information through cyclic subgraphs, and a temporal block for capturing temporal properties. We bolster the effectiveness of Cy2Mixer with mathematical evidence emphasizing that our cycle message-passing block is capable of offering differentiated information to the deep learning model compared to the message-passing block. Furthermore, empirical evaluations substantiate the efficacy of the Cy2Mixer, demonstrating state-of-the-art performances across various traffic benchmark datasets.

The PWLR Graph Representation: A Persistent Weisfeiler-Lehman scheme with Random Walks for Graph Classification

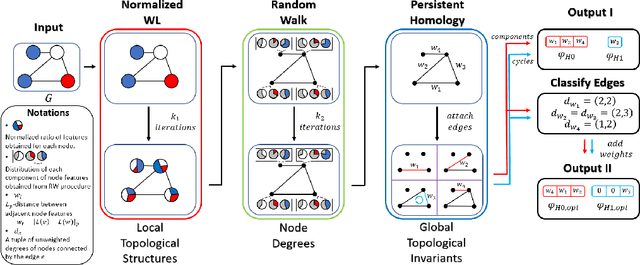
This paper presents the Persistent Weisfeiler-Lehman Random walk scheme (abbreviated as PWLR) for graph representations, a novel mathematical framework which produces a collection of explainable low-dimensional representations of graphs with discrete and continuous node features. The proposed scheme effectively incorporates normalized Weisfeiler-Lehman procedure, random walks on graphs, and persistent homology. We thereby integrate three distinct properties of graphs, which are local topological features, node degrees, and global topological invariants, while preserving stability from graph perturbations. This generalizes many variants of Weisfeiler-Lehman procedures, which are primarily used to embed graphs with discrete node labels. Empirical results suggest that these representations can be efficiently utilized to produce comparable results to state-of-the-art techniques in classifying graphs with discrete node labels, and enhanced performances in classifying those with continuous node features.