Youngho Woo
Topology-Informed Graph Transformer
Feb 03, 2024Abstract:Transformers have revolutionized performance in Natural Language Processing and Vision, paving the way for their integration with Graph Neural Networks (GNNs). One key challenge in enhancing graph transformers is strengthening the discriminative power of distinguishing isomorphisms of graphs, which plays a crucial role in boosting their predictive performances. To address this challenge, we introduce 'Topology-Informed Graph Transformer (TIGT)', a novel transformer enhancing both discriminative power in detecting graph isomorphisms and the overall performance of Graph Transformers. TIGT consists of four components: A topological positional embedding layer using non-isomorphic universal covers based on cyclic subgraphs of graphs to ensure unique graph representation: A dual-path message-passing layer to explicitly encode topological characteristics throughout the encoder layers: A global attention mechanism: And a graph information layer to recalibrate channel-wise graph features for better feature representation. TIGT outperforms previous Graph Transformers in classifying synthetic dataset aimed at distinguishing isomorphism classes of graphs. Additionally, mathematical analysis and empirical evaluations highlight our model's competitive edge over state-of-the-art Graph Transformers across various benchmark datasets.
The PWLR Graph Representation: A Persistent Weisfeiler-Lehman scheme with Random Walks for Graph Classification
Aug 29, 2022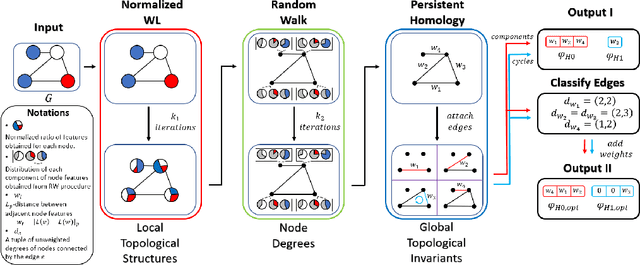



Abstract:This paper presents the Persistent Weisfeiler-Lehman Random walk scheme (abbreviated as PWLR) for graph representations, a novel mathematical framework which produces a collection of explainable low-dimensional representations of graphs with discrete and continuous node features. The proposed scheme effectively incorporates normalized Weisfeiler-Lehman procedure, random walks on graphs, and persistent homology. We thereby integrate three distinct properties of graphs, which are local topological features, node degrees, and global topological invariants, while preserving stability from graph perturbations. This generalizes many variants of Weisfeiler-Lehman procedures, which are primarily used to embed graphs with discrete node labels. Empirical results suggest that these representations can be efficiently utilized to produce comparable results to state-of-the-art techniques in classifying graphs with discrete node labels, and enhanced performances in classifying those with continuous node features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge