Dosang Joe
The PWLR Graph Representation: A Persistent Weisfeiler-Lehman scheme with Random Walks for Graph Classification
Aug 29, 2022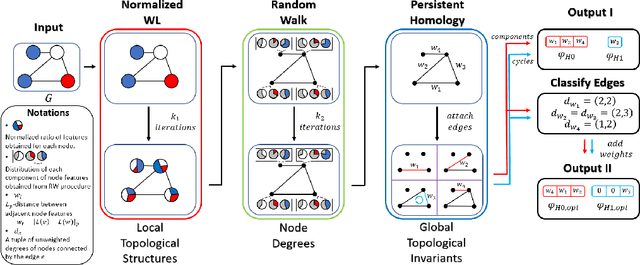



Abstract:This paper presents the Persistent Weisfeiler-Lehman Random walk scheme (abbreviated as PWLR) for graph representations, a novel mathematical framework which produces a collection of explainable low-dimensional representations of graphs with discrete and continuous node features. The proposed scheme effectively incorporates normalized Weisfeiler-Lehman procedure, random walks on graphs, and persistent homology. We thereby integrate three distinct properties of graphs, which are local topological features, node degrees, and global topological invariants, while preserving stability from graph perturbations. This generalizes many variants of Weisfeiler-Lehman procedures, which are primarily used to embed graphs with discrete node labels. Empirical results suggest that these representations can be efficiently utilized to produce comparable results to state-of-the-art techniques in classifying graphs with discrete node labels, and enhanced performances in classifying those with continuous node features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge